
- •Лекция 1
- •1.1. Основные определения Электрическая цепь
- •Электрический ток
- •Напряжение
- •Мощность и энергия
- •Схемы электрической цепи
- •Идеализированные пассивные элементы Резистивный элемент
- •Вольт-амперная характеристики резистора с линейным сопротивлением
- •Лекция 2 Емкостный элемент
- •Индуктивный элемент
- •Закон электромагнитной индукции:
- •Дуальные элементы цепи
- •Идеализированные активные элементы
- •Идеальный источник тока
- •Схемы замещения реальных источников
- •Управляемые источники тока и напряжения
- •Компонентные и топологические уравнения Законы Кирхгофа
- •Графы схем электрических цепей
- •Определение числа независимых узлов и контуров.
- •Основные задачи теории цепей
- •Понятие об уравнениях электрического равновесия
- •Лекция 4 Линейные электрические цепи при гармоническом воздействии
- •Понятие о среднем, средневыпрямленном и действующем значении гармонических токов и напряжений
- •Метод комплексных амплитуд
- •Комплексные изображения гармонических функций времени
- •Операции над комплексными изображениями гармонических функций
- •Лекция 5
- •Комплексная схема замещения цепи. Законы Ома и Кирхгофа в комплексной форме
- •Порядок анализа цепи методом комплексных амплитуд
- •Идеализированные пассивные элементы при гармоническом воздействии Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Лекция 6 Анализ простейших линейных цепей при гармоническом воздействии Последовательная rl-цепь
- •Последовательная rc – цепь
- •Последовательная rlc – цепь
- •Параллельная rlc – цепь
- •Делители напряжения и тока Делитель напряжения
- •Лекция 7 Энергетические процессы в простейших цепях при гармоническом воздействии Аналогии между механическими и электромагнитными процессами
- •Мгновенная мощность пассивного двухполюсника при гармоническом воздействии.
- •Активная, реактивная, полная и комплексная мощности
- •Баланс мощностей
- •Согласование источника энергии с нагрузкой
- •Лекция 8 Преобразования электрических цепей
- •Участки цепей с последовательным соединением элементов
- •Участки цепей с параллельным соединением элементов
- •Участки цепей со смешанным соединением элементов
- •Эквивалентное преобразование треугольника сопротивлений в звезду и обратное (самостоятельно)
- •Последовательная и параллельная схемы замещения пассивного двухполюсника
- •Перенос источников
- •Лекция 9 Цепи с взаимной индуктивностью
- •Понятие об одноименных зажимах
- •Коэффициент связи между индуктивными катушками
- •Цепи с взаимной индуктивностью при гармоническом воздействии
- •Эквивалентные преобразования участков цепей со связанными индуктивностями
- •Понятие о линейных трансформаторах
- •Лекция 10 Комплексные частотные характеристики линейных электрических цепей Понятие о комплексных частотных характеристиках
- •Комплексные частотные характеристики идеализированных двухполюсных пассивных элементов
- •Кчх цепей с одним реактивным элементом
- •Комплексный коэффициент передачи по напряжению
- •Логарифмические ачх и фчх
- •Лекция 11 Последовательный колебательный контур
- •Резонансная частота, характеристическое сопротивление и добротность контура
- •Энергетические процессы в последовательном колебательном контуре
- •Комплексные частотные характеристики
- •Передаточные характеристики контура
- •Лекция 12 Параллельный колебательный контур
- •Параллельный колебательный контур с разделенной индуктивностью
- •П араллельный колебательный контур с разделенной емкостью
- •Лекция 13 Методы формирования уравнений электрического равновесия цепи
- •Метод контурных токов (кт)
- •Метод узловых напряжений
- •Формирование уравнений электрического равновесия цепей с зависимыми источниками
- •Лекция 14 Основные теоремы теории цепей Принцип наложения (суперпозиции)
- •Теорема взаимности (обратимости)
- •Теорема компенсации
- •Теорема об эквивалентном источнике
- •Лекция 15 Многополюсники и цепи с многополюсными элементами
- •Классификация и схемы включения многополюсников
- •Основные уравнения и первичные параметры линейных неавтономных многополюсников
- •Основные уравнения и системы первичных параметров проходных четырехполюсников Классификация проходных четырехполюсников
- •Основные уравнения и основные параметры неавтономных проходных четырехполюсников
- •Методы определения первичных параметров четырехполюсников
- •Лекция 16 Первичные параметры составных четырехполюсников
- •Схемы замещения неавтономных проходных четырехполюсников
- •Автономные проходные четырехполюсники
- •Характеристические параметры и комплексные частотные характеристики (кчх) неавтономных проходных четырехполюсников к чх четырехполюсников при произвольной нагрузке
- •Характеристические сопротивления неавтономного проходного четырехполюсника
- •Характеристические постоянные передачи неавтономного проходного четырехполюсника
Лекция 11 Последовательный колебательный контур
П
L
оследовательный колебательный контур представляет собой электрическую цепь, содержащую реальную индуктивную катушку и конденсатор, включенные последовательно с источником энергии:П
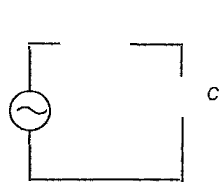

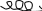 ерейдем
к схеме замещения:
ерейдем
к схеме замещения:
можно использовать последовательную и параллельную схемы замещения каждого элемента:
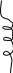

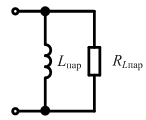
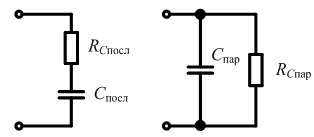

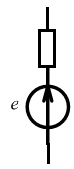
Ri
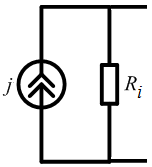
В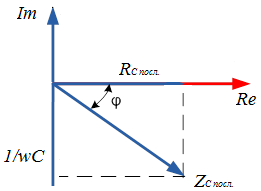 екторные
диаграммы комплексного сопротивления
индуктивной катушки и конденсатора:
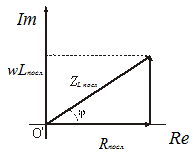
екторные
диаграммы комплексного сопротивления
индуктивной катушки и конденсатора:
Степень приближения реального элемента к идеальному количественно оценивают добротностью:
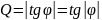 ;
0<Q<∞.
;
0<Q<∞.
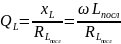 ;
;
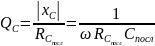 .
.
На практике:
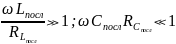 .
.
Экспериментально
установлено, что
 ,
а при высокой добротности QLC>>1;
,
а при высокой добротности QLC>>1;
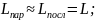
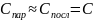 .
.
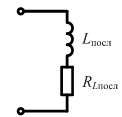
Поэтому для анализа процессов в последовательном колебательном контуре удобно воспользоваться последовательными схемами замещения всех элементов:
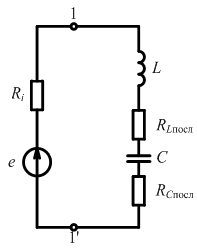
Пренебрегая
Ri
и объединяя сопротивления потерь контура
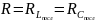 ,
получим последовательную схему замещения
последовательного колебательного
контура:
,
получим последовательную схему замещения
последовательного колебательного
контура:

i – ток контура;
u – напряжение контура.
Z=Z11 – входное сопротивление контура.
Понятие о резонансе
В электрических цепях, содержащих реактивные элементы различного вида, амплитуда отклика (токов, напряжений) может резко увеличиваться, когда частота внешнего воздействия достигает определенных значений.
Явление резкого возрастания амплитуды отклика цепи на некоторых частотах называется амплитудным резонансом.
По отношению к разным откликам (токам или напряжениям) резонансные частоты цепи могут быть близкие, но разные.
В теории цепей, как и в физике при гармоническом воздействии, используют понятие фазового резонанса.
Фазовым резонансом называют такой режим работы электрической цепи, содержащей емкости и индуктивности, при котором ее комплексное входное сопротивление имеет чисто резистивный характер, и, следовательно, сдвиг фаз между током и напряжением на входе равен нулю.
Цепи, обладающие амплитудным резонансом, называются резонансными или колебательными.
Простейшая такая цепь – это последовательный колебательный контур.
Резонансная частота, характеристическое сопротивление и добротность контура
В
ВТ07
XL=
XC=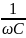
ВОТУ
xL=
xC=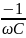
соответствии с определением фазового резонанса мнимая составляющая входного сопротивления последовательного колебательного контура
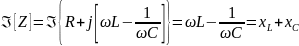
должна быть равна нулю, когда частота внешнего
воздействия равна резонансной частоте контура
т.е.
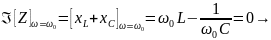
 .
.
На резонансной частоте полное сопротивление
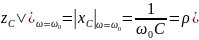 равно
полному сопротивлению индуктивности
равно
полному сопротивлению индуктивности
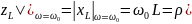
Величина ρ называется характеристическим сопротивлением контура.
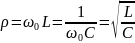
На резонансной частоте входное сопротивление контура имеет чисто резистивный характер и равно сопротивлению потерь контура:
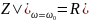
Амплитуда тока на резонансной частоте:
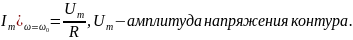
Амплитуды напряжения на реактивных элементах контура на резонансной частоте:
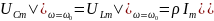
Отношение амплитуды напряжения на реактивном элементе к амплитуде напряжения на контуре на резонансной частоте называется добротностью контура:
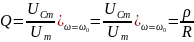
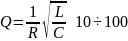 ,
поэтому
,
поэтому
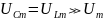 .
.
Добротность
контура может быть выражена через
добротность элементов на резонансной
частоте: (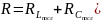
величина
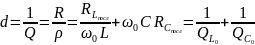 ,
,
 .
.
Добротность контура не может превышать добротность его элементов на резонансной частоте.
