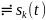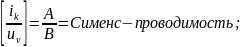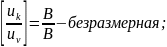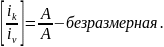- •Лекция 1
- •1.1. Основные определения Электрическая цепь
- •Электрический ток
- •Напряжение
- •Мощность и энергия
- •Схемы электрической цепи
- •Идеализированные пассивные элементы Резистивный элемент
- •Вольт-амперная характеристики резистора с линейным сопротивлением
- •Лекция 2 Емкостный элемент
- •Индуктивный элемент
- •Закон электромагнитной индукции:
- •Дуальные элементы цепи
- •Идеализированные активные элементы
- •Идеальный источник тока
- •Схемы замещения реальных источников
- •Управляемые источники тока и напряжения
- •Компонентные и топологические уравнения Законы Кирхгофа
- •Графы схем электрических цепей
- •Определение числа независимых узлов и контуров.
- •Основные задачи теории цепей
- •Понятие об уравнениях электрического равновесия
- •Лекция 4 Линейные электрические цепи при гармоническом воздействии
- •Понятие о среднем, средневыпрямленном и действующем значении гармонических токов и напряжений
- •Метод комплексных амплитуд
- •Комплексные изображения гармонических функций времени
- •Операции над комплексными изображениями гармонических функций
- •Лекция 5
- •Комплексная схема замещения цепи. Законы Ома и Кирхгофа в комплексной форме
- •Порядок анализа цепи методом комплексных амплитуд
- •Идеализированные пассивные элементы при гармоническом воздействии Резистивный элемент
- •Емкостный элемент
- •Индуктивный элемент
- •Лекция 6 Анализ простейших линейных цепей при гармоническом воздействии Последовательная rl-цепь
- •Последовательная rc – цепь
- •Последовательная rlc – цепь
- •Параллельная rlc – цепь
- •Делители напряжения и тока Делитель напряжения
- •Лекция 7 Энергетические процессы в простейших цепях при гармоническом воздействии Аналогии между механическими и электромагнитными процессами
- •Мгновенная мощность пассивного двухполюсника при гармоническом воздействии.
- •Активная, реактивная, полная и комплексная мощности
- •Баланс мощностей
- •Согласование источника энергии с нагрузкой
- •Лекция 8 Преобразования электрических цепей
- •Участки цепей с последовательным соединением элементов
- •Участки цепей с параллельным соединением элементов
- •Участки цепей со смешанным соединением элементов
- •Эквивалентное преобразование треугольника сопротивлений в звезду и обратное (самостоятельно)
- •Последовательная и параллельная схемы замещения пассивного двухполюсника
- •Перенос источников
- •Лекция 9 Цепи с взаимной индуктивностью
- •Понятие об одноименных зажимах
- •Коэффициент связи между индуктивными катушками
- •Цепи с взаимной индуктивностью при гармоническом воздействии
- •Эквивалентные преобразования участков цепей со связанными индуктивностями
- •Понятие о линейных трансформаторах
- •Лекция 10 Комплексные частотные характеристики линейных электрических цепей Понятие о комплексных частотных характеристиках
- •Комплексные частотные характеристики идеализированных двухполюсных пассивных элементов
- •Кчх цепей с одним реактивным элементом
- •Комплексный коэффициент передачи по напряжению
- •Логарифмические ачх и фчх
- •Лекция 11 Последовательный колебательный контур
- •Резонансная частота, характеристическое сопротивление и добротность контура
- •Энергетические процессы в последовательном колебательном контуре
- •Комплексные частотные характеристики
- •Передаточные характеристики контура
- •Лекция 12 Параллельный колебательный контур
- •Параллельный колебательный контур с разделенной индуктивностью
- •П араллельный колебательный контур с разделенной емкостью
- •Лекция 13 Методы формирования уравнений электрического равновесия цепи
- •Метод контурных токов (кт)
- •Метод узловых напряжений
- •Формирование уравнений электрического равновесия цепей с зависимыми источниками
- •Лекция 14 Основные теоремы теории цепей Принцип наложения (суперпозиции)
- •Теорема взаимности (обратимости)
- •Теорема компенсации
- •Теорема об эквивалентном источнике
- •Лекция 15 Многополюсники и цепи с многополюсными элементами
- •Классификация и схемы включения многополюсников
- •Основные уравнения и первичные параметры линейных неавтономных многополюсников
- •Основные уравнения и системы первичных параметров проходных четырехполюсников Классификация проходных четырехполюсников
- •Основные уравнения и основные параметры неавтономных проходных четырехполюсников
- •Методы определения первичных параметров четырехполюсников
- •Лекция 16 Первичные параметры составных четырехполюсников
- •Схемы замещения неавтономных проходных четырехполюсников
- •Автономные проходные четырехполюсники
- •Характеристические параметры и комплексные частотные характеристики (кчх) неавтономных проходных четырехполюсников к чх четырехполюсников при произвольной нагрузке
- •Характеристические сопротивления неавтономного проходного четырехполюсника
- •Характеристические постоянные передачи неавтономного проходного четырехполюсника
Лекция 10 Комплексные частотные характеристики линейных электрических цепей Понятие о комплексных частотных характеристиках
В линейных электрических цепях воздействие задается с помощью независимых источников тока и напряжения. Откликами цепи на оказанное воздействие являются все токи и напряжения в цепи. Однако, часто интересуют только токи или напряжения на отдельных элементах, называемых нагрузками.
Выделим из цепи все независимые источники и нагрузки:
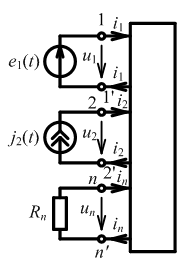
Входом цепи называется пара зажимов (полюсов), к которым подключен независимый источник.
Пара зажимов, служащих для подключения нагрузки, т.е. ветви, напряжение или ток которой необходимо определить, называется выходом.
Одна и та же пара зажимов может быть как входной, так и выходной, например, если необходимо определить ток независимого источника напряжения.
Входные и выходные пары зажимов иногда называют сторонами или портами многополюсника.
Особенности портов многополюсника:
1) ток, втекающий через один зажим порта, равен току, вытекающему через другой зажим этого же порта;
2) между парами полюсов, принадлежащих к разным портам, не должно быть никаких внешних по отношению к многополюснику соединений.
Зажимы, образующие одну сторону многополюсника, обозначают одинаковыми цифрами: 1 — 1', 2 — 2',… n — n'.
Различают односторонние, двусторонние и n – сторонние многополюсники.
Р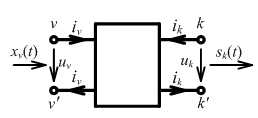 ассмотрим
двусторонний многополюсник или
двусторонний четырехполюсник:
ассмотрим
двусторонний многополюсник или
двусторонний четырехполюсник:
Внешнее
воздействие задано на паре полюсов ν
—
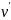 :
x(t)
= xv(t);
:
x(t)
= xv(t);
реакция
на паре полюсов k
—
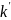 :
s(t)
= sk(t).
:
s(t)
= sk(t).
Если ν = k, то получим односторонний многополюсник или двухполюсник.
Будем рассматривать далее только случай гармонического внешнего воздействия.
Комплексной частотной характеристикой (частотным коэффициентом передачи) цепи называется отношение комплексных изображений отклика и воздействия:
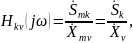
где
 mk
≓
sk(t);
k
=
mk
mk
≓
sk(t);
k
=
mk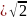 .
.
Размерность КЧХ разная:
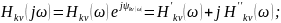
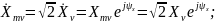
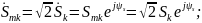
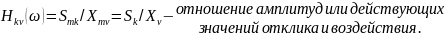
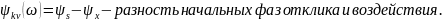
Если
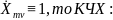
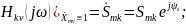
Таким образом, КЧХ цепи численно равна комплексной амплитуде реакции цепи на воздействие в виде единичной гармонической функции:
xv(t) = cos ωt, т.е. с единичной амплитудой Xmv = 1 и нулевой начальной фазой ψх = 0. Зависимость модуля Нkv(ω) КЧХ от частоты называется амплитудно – частотной характеристикой (АЧХ) цепи; зависимость аргумента ψkv(ω) КЧХ от частоты называется фазо – частотной характеристикой (ФЧХ) цепи.
При гармоническом представлении КЧХ цепи обычно строят отдельно АЧХ Нkv(ω), ФЧХ ψkv(ω) или вещественную Н'kv(ω) и мнимую H''kv(ω) составляющие.
КЧХ можно представить в виде одной зависимости – годографа КЧХ.
Годограф КЧХ – это геометрическое место концов вектора Нkv(jω) при изменении частоты от ω = 0 до ω = ∞.
Пример годографа:
К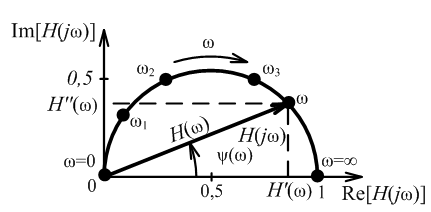 ЧХ
цепи делятся на входные
и передаточные.
Если воздействие и отклик рассматриваются
на одних зажимах, то КЧХ – входная; если
на разных, то передаточная.
ЧХ
цепи делятся на входные
и передаточные.
Если воздействие и отклик рассматриваются
на одних зажимах, то КЧХ – входная; если
на разных, то передаточная.
Различают два вида входных КЧХ:
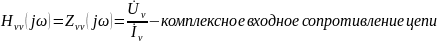
относительно зажимов ν — ;
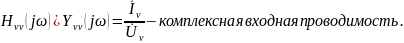
Передаточные характеристики цепи:
комплексный коэффициент передачи по напряжению
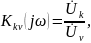
комплексный коэффициент передачи по току
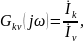
комплексное передаточное сопротивление
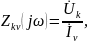
и комплексная передаточная проводимость

КЧХ линейной электрической цепи не зависят от амплитуды и начальной фазы внешнего воздействия, а определяются структурой и параметрами элементов цепи.
Знание КЧХ позволяет определить реакцию цепи на оказанное воздействие в 3 этапа:
xν(t)
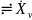
k=
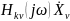
k