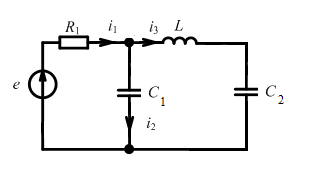
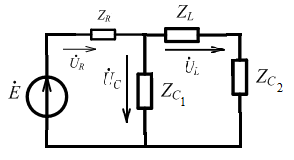
Комплексная схема замещения цепи. Законы Ома и Кирхгофа в комплексной форме

Зная комплексное сопротивление или комплексную проводимость участка цепи и комплексную амплитуду тока или напряжения, можно найти неизвестную комплексную амплитуду напряжения или тока:

Это формулы закона Ома в комплексной форме; они же компонентные уравнения ветвей цепи в комплексной форме – алгебраические.

Если в исходной моделирующей цепи заменить идеализированные пассивные элементы, а источники энергии их комплексными амплитудами, получим комплексную схему замещения цепи:

u_C2

1

2

Первый закон Кирхгофа:

Второй закон Кирхгофа: ;

Суммированию гармонических функций времени соответствует суммирование их комплексных амплитуд.

I – й закон Кирхгофа:

где k — номер ветви, подключенной к рассматриваемому узлу.

Сумма комплексных амплитуд токов всех ветвей, подключенных к каждому из узлов электрической цепи, равна нулю.

II – й закон Кирхгофа:

где — номер ветви, входящей в рассматриваемый контур.

Сумма комплексных амплитуд напряжений всех ветвей, входящих в любой контур цепи, равна нулю.

2 – формулировка:

Сумма комплексных амплитуд напряжений на всех элементах любого контура моделирующей цепи, кроме источников напряжения, равна сумме комплексных ЭДС всех входящих в контур источников напряжения.

Учет знаков при суммировании в I и II – м законах Кирхгофа аналогичен правилам для мгновенных значений (рис.).

Используя законы Ома и Кирхгофа, можно построить основную систему уравнений электрического равновесия цепи для комплексных амплитуд токов и напряжений всех ветвей, содержащей 2p – p_ин – p_ит уравнений.

Порядок анализа цепи методом комплексных амплитуд

1) Переход от гармонических токов и напряжений всех ветвей к их комплексным изображениям (комплексным амплитудам или комплексным действующим значениям) и к комплексной схеме замещения;

2) составление уравнений электрического равновесия цепи для комплексных изображений токов и напряжений;

3) решение системы алгебраических уравнений относительно искомых комплексных изображений токов или напряжений;

4) переход от комплексных изображений искомых токов или напряжений к их гармоническим оригиналам.

Идеализированные пассивные элементы при гармоническом воздействии Резистивный элемент

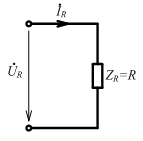
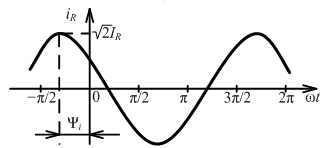
З 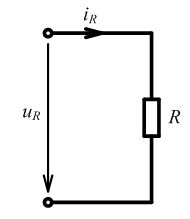адано:

найти: i_R , Z_R

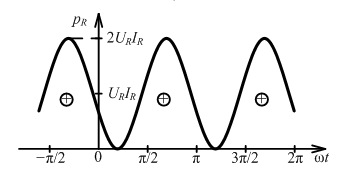
М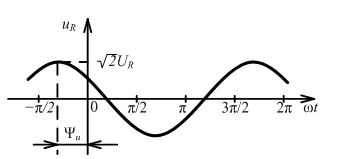 гновенная мощность:

|

( |=

С

Средняя мощность

редняя мощность на периоде называется активной мощностью:

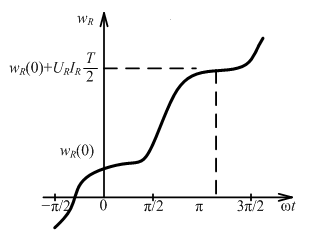
Энергия, поступившая в резистивный элемент:

Комплексные ток и напряжение резистивного элемента:

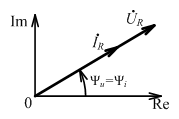
Комплексное сопротивление:

;

φ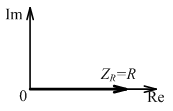 _R  = ψ_u − ψ_i = 0; r_R = R, x_R  =  0.

Схема замещения

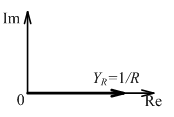
Комплексная проводимость резистивного элемента:

Y_R = 1/Z_R  = 1/R = G.

Емкостный элемент

;

.

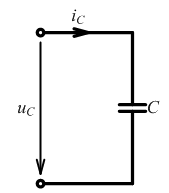
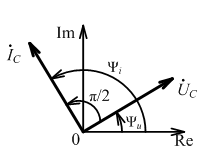
ψ_i = ψ_u + π/2, - ток емкости опережает по фазе напряжение на 90°

I_C = ωCU_C

М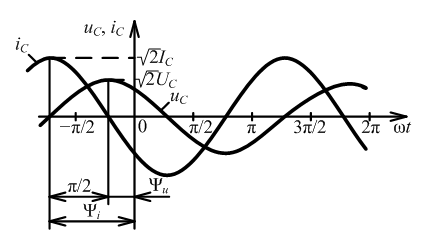 гновенная мощность:

;

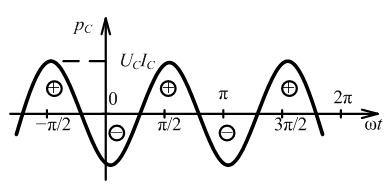
Энергия:

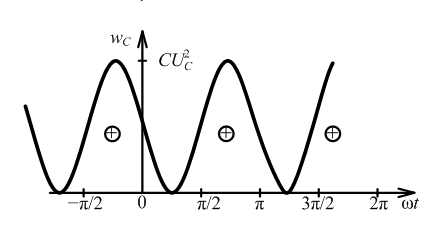
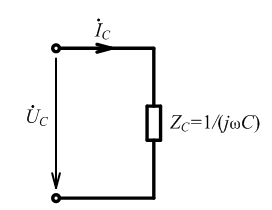
Комплексные ток и напряжение емкости:

;

Комплексное сопротивление емкости:

Комплексная схема замещения

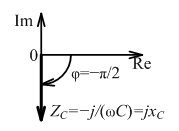
r_C = 0; х_C = −1/(ωС); z_C = 1/(ωC); φ_C = −π/2

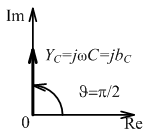
Комплексная проводимость емкости:

; _C = π/2;