23

1. Основные понятия о форме и размерах Земли. Референц-эллипсоид Красовского. Системы координат, применяемые в геодезии.

Земля не является правильным геометрическим телом. Её физическая поверхность очень сложная и её невозможно выразить математической формулой. Поэтому в геодезии введено понятие уровенной поверхности – это выпуклая поверхность, перпендикулярная к направлению силы тяжести в каждой точке. Уровненную поверхность можно представить как водную поверхность океана, моря, озера в спокойном состоянии. Поверхность воды Мирового океана, мысленно продолженная под сушей, названа поверхностью геоида, а тело, ограниченное ею наз. геоидом. Земля сплюснута у полюсов, поэтому в качестве математической поверхности принимают поверхность эллипсоида вращения, т. е. тела, получают от вращения эллипса вокруг его малой оси, кот по форме близко подходит к поверхности геоида. Размеры эллипсоида характеризуются длинами его большой полуоси - а, малой полуоси – b и сжатием α, определяем по формуле:

α= (а- b)/ а.

В 1940 г. геодезистами под руководством проф. Красовского были получены наиболее точные и достоверные размеры земного эллипсоида, принятые для геодезических работ. При приближенных расчетах поверхность эллипсоида принимают за поверхность шара с радиусом 6371,1 км, округляя, получают 6370 или 6400 км. Для небольших участков земной поверхности поверхность эллипсоида принимают за плоскость.

Положение точек земной поверхности на карте и плане определяется координатами (географическими и прямоугольными, полярными и биполярными).

Географическими координатами являются широта и долгота точки.

Широты бывают северные и южные, изменяются от 0⁰ до 90⁰.

Долготы бывают восточные и западные, измеряются от 0⁰ на восток и на запад до 180⁰. Линия, проходящая через точки с одинаковыми широтами, называется параллелью, а с одинаковыми долготами – меридианом.

Д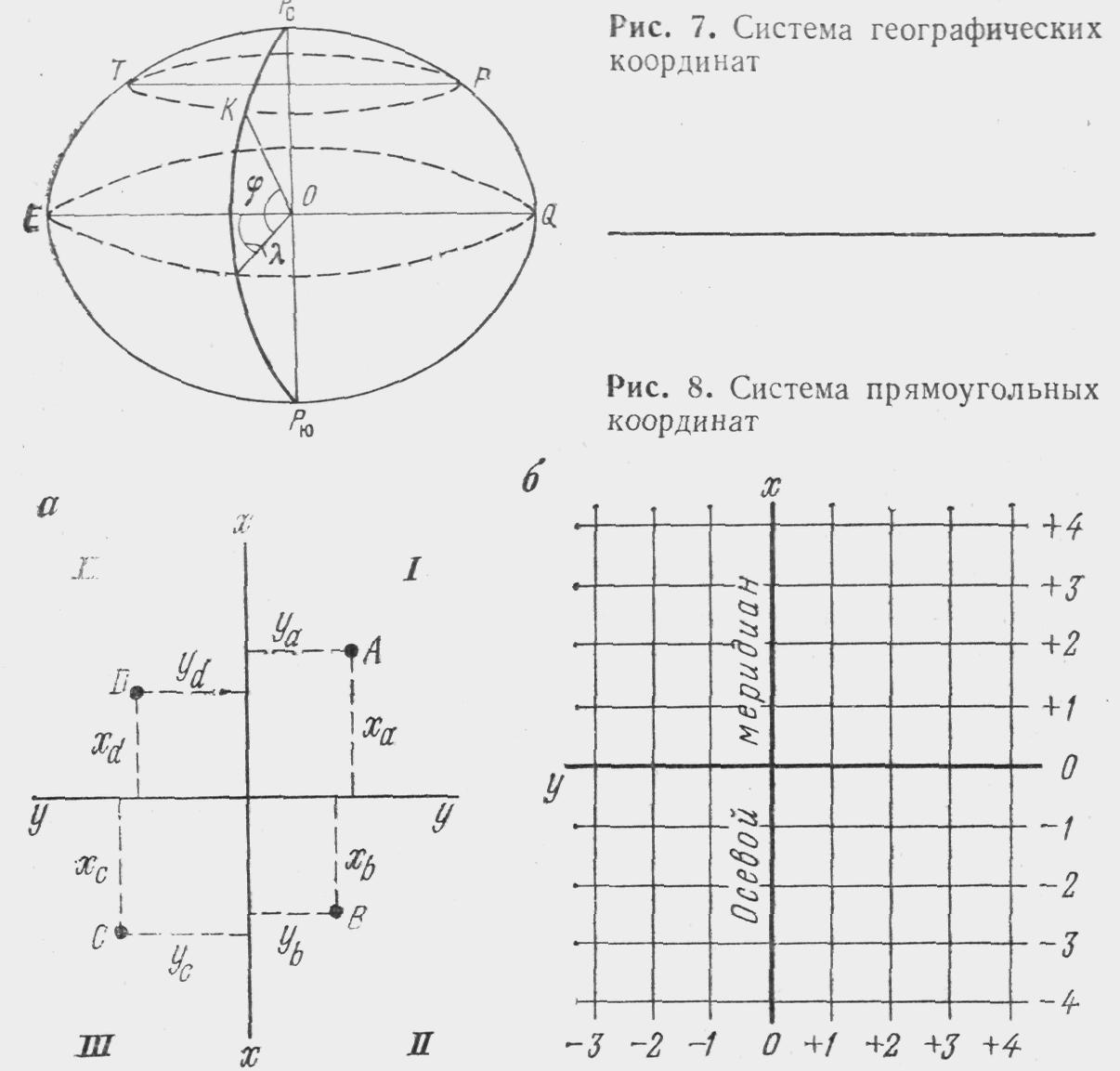 ля составления карты на большую территорию строят географическую сетку меридианов и параллелей, для составления планов и карт в инженерной геодезии пользуются системой прямоугольных координат. Положение точки определяется относительно осей прямоугольных координат: оси абсцисс - х и оси ординат - у. Знаки координат зависят от четверти, в которых находится точка (I четверть х положительный, у положительный; II – х отрицательный, у положительный; III – х отрицательный, у отрицательный; IV – х положительный, у отрицательный). В государственной системе за ось ординат принимают линию экватора, за ось абсцисс – направление меридиана, принимаемого за осевой. Углы в геодезии для ориентирования линий (дирекционные углы) отсчитывают от вертикальной оси по ходу часовой стрелки. Помимо осей координат, на бумаге через определенное расстояние проводят линии, параллельные осям координат составляют прямоугольную сетку. Эта сетка нужна для составления плана.

Положение точки на земной поверхности или на плоскости определяется известными величинами (координатами). В геодезии используют несколько систем координат: географические, прямоугольные, полярные и биполярные.

В географической системе положение точки, лежащей на земной поверхности, определяется географической широтой и долготой.

На эллипсоиде РсРю — полярная ось, а точки Рс и Рю — северный и южный полюсы. Линия EQ, называется экваториальной осью.

Плоскость ЕQ, называется экватором. Окружность ТР называется параллелью. Ли­ния пересечения поверхности эллипсоида с плоскостью, проходящей через данную точку К и полярную ось, называется меридианом данной точки. Положение точки на земной поверхности определяется пересечением параллели и меридиана, проходящих через нее.

Угол φ называется географической широтой. Для определения долгот точек один из меридианов принимают за начальный или нулевой. Это меридиан, который проходит через центр Гринвичской обсервато­рии, находящейся вблизи Лондона. Угол λ называется географ долготой. Самое широкое применение в геодезии получила прямоугольная система координат (рис.). Проведем на плоскости прямую хх и пер­пендикулярно к ней — уу.

Прямая хх— наз. осевой меридиан, а уу — перпендикулярная к оси абсцисс, называется осью ординат или осью игреков. Точка пересечения осей принимается за начало координат. y — абсцисса, х — ордината.

Чтобы определить положение любой точки А на пло­скости по отношению к осям координат, нужно опустить перпендикуляры из этой точки на оси координат. Расстоя­ние от точки А до оси у называется абсциссой то­чки А, а до оси х—ординатой и обозначаются соответственно ха и уа.

Сущность полярной системы координат заклю­чается в следующем. На горизонтальной плоскости через выбранную точку О (рис. 9), называемую полюсом, проведем линию Ох, называемую полярной осью. Отложим по ходу часовой стрелки от оси Ох угол β₁ и проведем прямую через полюс О. Отложив на этой пря­мой расстояние r₁ получим положение искомой точки А. Расстояние О А называется радиусом - вектором точки А.

В биполярной системе координат на плоско­сти выбирают два полюса О₁ и О₂ (рис. 10), которые со­единяют прямой, называемой полярной осью. Для по­лучения положения точки А откладывают от полярной

оси углы β₁ и β₂ и проводят через полюсы радиусы - век­торы r₁ и r₂. На их пересечении получим искомую то­чку А.

2. Абсолютные и относительные высоты точек земной поверхности. Превышение. Высотные геодезические сети.

При использовании изображения земной поверхности на плане или карте для составления проектов ЗУ нужно иметь представление о неровностях земной поверхности. Неровности поверхности характеризуются высотами точек. Высотой точки называется отрезок отвесной линии (расстояние) от этой точки до уровенной поверхности, принятой за начало счёта высот. Высоты точек земной поверхности, от­считываемые от среднего уровня Балтийского моря, отмеченного чертой Крон­штадтского футштока, называют абсо­лютными. Отрезки отвесных линий являются абсолютными высотами точек местности. Если высоты отсчитывают от какой-либо условно выбранной уровенной поверхности, то их называют относительными или условными. Отрезки отвесных линий яв­ляются относительными высотами точек ме­стности. Разность абсолютных или относительных высот точек называется превышением, которое обозначается буквой h.

Высоты точек земной поверхности преимущественно положительны и лишь для точек, располагающихся ниже уровенной поверхности океана отрицательны. Если для небольшого расстояния между точками не учитывать кривизну земли и уровенную поверхность принять за плоскость, то превышение точки А над точкой В можно вычислить по горизонтальному проложению s и углу наклона ۷, пользуясь формулой:

h= s tg۷.

А высоту точки А, зная высоту точки В по формуле:

Н_А=Н_В+h=Н_В+s tg۷.

Высотные геодезические сети создаются в основном методами геометрического и тригонометрического нивелирования. Сети геометрического нивелирования подразделяются на государственную нивелирную сеть и сети технического нивелирования. Гос нивелирные сети делятся на 4 класса. Линии I класса прокладываются по направлениям, связывающим далекие друг от друга пункты и основные морские водомерные посты. Нивелирная сеть II класса опирается на пункты I класса. Линии I и II классов прокладываются по местам, наиболее удобным для нивелирования (вдоль железных, шоссейных дорог, больших рек). Нивелирная сеть III класса опирается на пункты I и II классов, и образуют полигоны с периметром 150 км. Нивелирные ходы IV класса прокладываются в одном направлении между пунктами старших классов. Длины этих ходов не должны превышать 50 км. Пункты этого класса являются высотным обоснованием для топографических съёмок. Пункты нивелирования всех классов закрепляются реперами и марками через каждые 5 км.