Квадр формулы Гаусса

Численное интегрирование определённых интегралов

с высокой точностью. Квадратурные формулы

типа Гаусса.

Как было отмечено на предыдущей лекции численное вычисление определённых интегралов сводится к вычислению квадратурной суммы вида

где [a; b] – любой конечный или бесконечный отрезок числовой оси; р(х) – весовая функция, учитывающая особенности поведения подынтегральной функции; f(x) – произвольная гладкая функция ; A_k – квадратурные коэффициенты, x_k – квадратурные узлы..

Квадратурная сумма однозначно определяется 2n+1 параметром: n значений А_к, n – значений х_k и сам параметр n – число разбиений отрезка [a; b]. Чтобы получить более точный результат при вычислениях с помощью простейших квадратурных формул, следует дробить отрезок интегрирования на достаточно большое число интервалов. (Это наблюдалось, при рассмотрении простейших квадратурных формул трапеций и Симпсона)

Однако возможны и другие способы повышения точности квадратурных формул. Достижение точности можно добиться за счёт правильного или оптимального выбора узлов x_k и квадратурных коэффициентов A_k.

Если по условию задачи узлы можно выбирать произвольным образом и функция f(x) обладает высокой степенью гладкости, то для вычисления определённых интегралов применяют квадратурные формулы типа Гаусса.

Формула Гаусса.

Пусть необходимо вычислить определённый интеграл вида:

где f(x) – имеет высокую степень гладкости на интервале [-1; 1].

Данную задачу можно решить с помощью квадратурной формулы

.

Гауссом было доказано, что для достижения наивысшей точности результата интегрирования необходимо в качестве узлов квадратурной формулы взять корни многочлена Лежандра

.

Коэффициенты А_к при этом вычисляются по формулам

.

Рассмотрим применение этих формул.

При n=1 имеем одну узловую точку внутри отрезка [-1; 1], которая определяется из уравнения

Т.к. , то узловую точку находим из уравнения Отсюда

Т.к. , то .

При n=2 получаем две узловые точки внутри отрезка [-1; 1], которые определяется из уравнения

Преобразовав его получаем

.

Его решение . Т.к. ,

то общая формула для вычисления квадратурных коэффициентов приобретёт вид . Подставляя узловые точки, получаем:

при ;

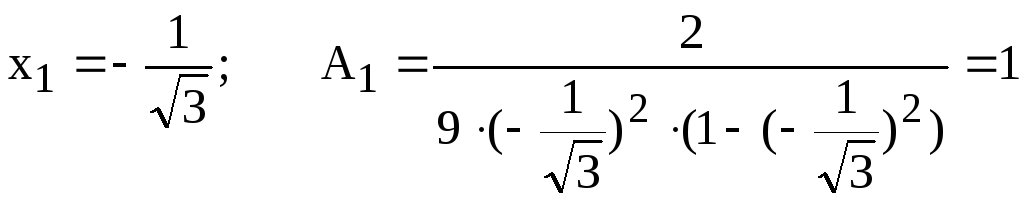при .

Для различного числа разбиения отрезка [-1; 1] можно получить таблицу узлов x_k и коэффициентов A_k. (Как это сделать будет показано на практическом занятии)

К-во точек разбиения	Узлы квадратурной формы	Коэффициенты квадратурной формы
n=1	x1=0	A1=2
n=2
n=3
n=4
n=5

В случае произвольного интервала интегрирования [a; b] (когда он не совпадает с отрезком [-1; 1]) предварительно делают замену переменной

.

А уже к преобразованному интегралу можно применить формулу Гаусса. Получим

,

где

– узлы квадратурной формулы Гаусса;

– соответствующие коэффициенты;

– остаток квадратуры.

Остаток квадратурной формулы Гаусса определяется по формуле

где

Пример. По формуле Гаусса вычислить интеграл I= (при n=5).

Решение.

Т.к. интервал интегрирования не совпадает с отрезком [-1; 1], применим

замену

.
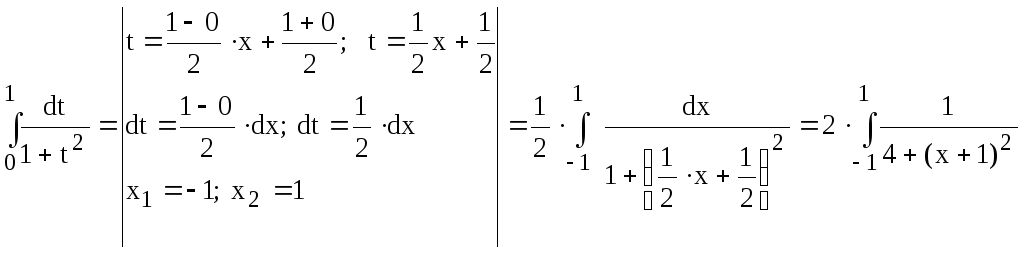