1.5 Рух мікрочастинки у водневоподiбному атомі
У
воднеподiбному атомi навколо ядра з
зарядом
(
-
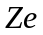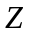порядковий номер хiмiчного елементу)
рухається тiльки один електрон. Потенцiйна
енергiя взаємодiї його з ядром дорiвнює:
.
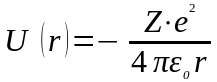(76)
На
рисунку 8 показано криву
.
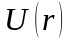З нього видно, що водневоподiбний атом
можна розглядати як своєрiдну потенцiйну
яму, обмежену потенцiйною кривою. Електрон
у цiй ямi володiє негативною енергiєю.
Пiдставляючи (76) у (14), одержимо рiвняння Шредiнгера, яке описує стацiонарний стан водневоподiбного атому:
.
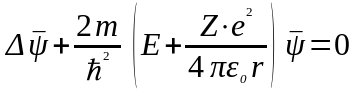(77)
Рис. 8. Залежнiсть енергiї взаємодiї електрону з ядром
воднеподiбного атома вiд вiдстанi.
Рiшення цього рiвняння дає наступні основні результати.
1. Електрон у водневоподiбному атомi володiє дискретним енергетичним спектром. Власнi значення енергiї визначаються формулою:
,
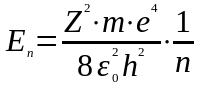(78)
де - головне квантове число.
На рисунку 8 показане розташування енергетичних рiвнiв у водневоподiбному атомi.
2. Орбiтальний момент кiлькостi руху електрона може приймати лише наступний ряд дискретних значень:
,
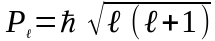(79)
де
-
орбiтальне
(азимутальне) квантове число.
Воно може приймати будь-які значення з наступного цiлочисельного ряду:
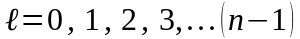(80)
- усього значень.
3.
Стан з
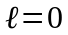(при будь-якому
)
прийнято називати
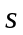-станом,
-
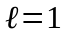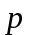-станом,
-
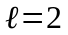d-станом,
-
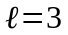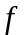-станом
і т.д.
4.
Орбiтальний момент кiлькостi руху може
орiєнтуватися вiдносно вибраного напрямку
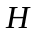лише таким чином, що проекцiя його на
цей напрямок цiлократна
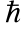(рис. 9):
.
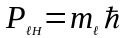(81)
Число
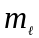зветься магнiтним
квантовим числом.
Воно може приймати усi цiлочисельнi
значення вiд
до
,
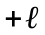включаючи нуль:
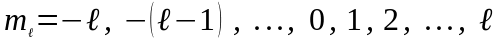(82)
-
усього
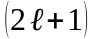значень.
Рис. 9. Орiєнтацiя орбiтального моменту кiлькостi руху вiдносно обраного напрямку Н.
Висновки
1.
Стан електорну у водневоподiбному атомi
визначається трьома квантовими числами
- головним
,
що характеризує енергiю
;
орбiтальним
,
що визначає орбiтальний момент кiлькостi
руху електрона
,
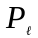та магнiтним
,
що характеризує орiєнтацiю
вiдносно вибраного напрямку.
2.
Цi стани описуються власними хвильовими
функцiями
,
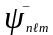якi є рiшеннями рiвняння Шредiнгера (77).
3.
Iмовiрнiсть знаходження електрону у
кульковому шарi товщиною
,
замкненому помiж
та
,
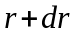дорiвнює добутку
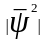на об'єм цього шару
:
.
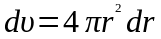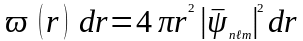(83)
Щільність
iмовiрностi знаходження електрону на
вiдстанi r
вiд ядра дорiвнює
.
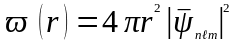Перехiд до багатоелектронних атомiв
У багатоелектронних атомах валентний електрон взаємодiє не тiльки з ядром, але й з iншими електронами, внаслiдок чого у виразi для потенцiйної енергiї з'являються додатковi члени, якi вiдповiдають цю взаємодiю. Наявнiсть таких членiв не дозволяє одержати точне рiшення рiвняння Шредiнгера. Тому вдаються до наближених методів рiшення.
У
простiших випадках рахують, що потенцiал
взаємодiї валентного електрону з
електронною оболонкою являється
приблизно сферично симетричним i задачу
вирiшують, як для водневоподiбного атому.
Природньо, що таке рiшення повинно мати
багато спiльного з рiшенням задачi про
водневоподiбний атом. Зокрема, стан
електрону у атомi характеризується
завданням таких же трьох квантових
чисел, що й стан у атомi водню. Проте
вiдхилення потенцiалу поля вiд чисто
кулонiвського, що викликане взаємодiєю
електронiв мiж собою, призводить до того,
що енергiя електрону стає функцiєю не
тiльки головного, але й орбiтального
квантового числа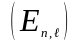
.
Спiн електрону
Iз
загальних принципiв квантової механiки
випливає, що крiм маси та заряду, електрон
повинен володiти власним моментом
кiлькостi руху
:
.
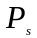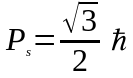(84)
Гiпотеза про iснування цього моменту була вперше висунута у 1927 р. Гаудсмiтом та Уленбеком для пояснення законо-мiрностей у лiнiйчастих спектрах та експериментально доведена Штерном і Герлахом. На початку припускалось, що власний момент кiлькостi руху виникає внаслiдок обертання електрона навколо власної осi. Тому вiн одержав назву спiну (вiд англiйського "spin" - обертання, веретено). Проте таке уявлення про спiн є первiсним, невiд'ємною властивiстю електрону, що не зводиться до бiльш простого.
Проекцiя спiну на напрямок може мати лише два значення:
.
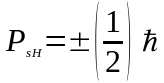(85)
По аналогiї з формулою (81), цей вираз можна записати таким чином:
,
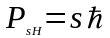(86)
де
називається спiновим квантовим числом.
Iз порiвняння (85) та (86) видно, що
може приймати тiльки два значення:
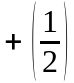та
.
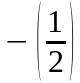