ВСТУП

Мета цього тому підручника – вивчення фiзичних явищ, що лежать у основi принципа дiї приладiв елементної бази сучасної електронної технiки.

За допомогою підручника читачі зможуть:

знати – фiзику явищ, що лежать у основi роботи електронних приладiв;

вмiти – використовувати цi знання для визначення фiзичних принципiв дiї приладiв електронної технiки та використання їх при створеннi електронної апаратури;

пам'ятати – без знання фiзичних основ спецiальностi неможлива творча робота сучасного спецiалiста в умовах бурхливого розвитку елементної бази електронiки та областей її застосування.

Електронними звуться прилади, принцип роботи яких оснований на використаннi явищ, що виникають у процесi одержання потокiв електронiв, керування рухом цих потокiв та їх перетворення на елементах конструкцiї приладiв.

В залежностi вiд властивостей середовища, в якому вiдбувається рух електронних потокiв, електроннi прилади дiляться на вакуумнi, газорозряднi (iоннi), напiвпровiдниковi. Впливати на рух електронiв, отже, керувати їх потоками, можливо за допомогою електричних та магнiтних полiв, а також створення матерiальних перешкод на їх шляху.

Розвиток електронних приладів був забезпечений вивченням таких фізичних явищ, як емісія електронів з твердого тіла, електричний розряд у газах, плазма, а також розвитком фізики твердого тіла, напівпровідників, оптики тощо. Класифікацію електронних приладів за фізичними явищами, на яких вони засновані, можна представити схемою на рисунку 1.

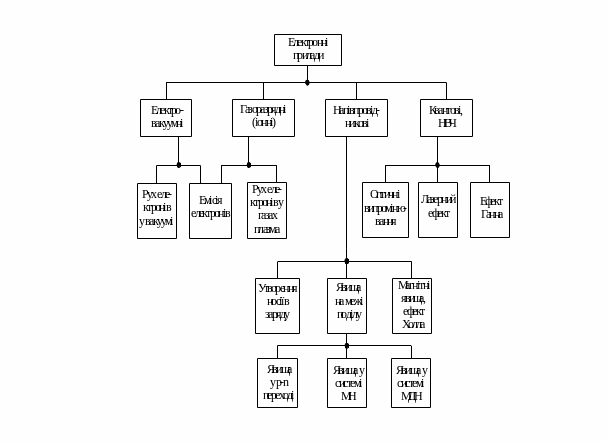
Рис. 1. Класифікація фізичних явищ, що лежать у основі

дії електронних приладів.

Сучасні електронні галузі – наноелектроніка, засоби телекомунікацій та інші – засновані значною мірою на використанні напівпровідникових, квантових та НВЧ приладів. Тому фізичні явища, що забезпечують принцип дії цих приладів, є об'єктом вивчення у даному томі.

Кінцева мета – знання властивостей твердого тіла та p-n-переходів як основи твердотільних приладів. Для її досягнення треба знати закони поведінки мікрочастинок під впливом середовища та зовнішніх факторів. Тому надані знання з основ квантової механіки, статистичної фізики, зонної теорії, фізики твердого тіла тощо [1,2].

Розділ 1 основи квантової механiки

1.1 Подвiйнiсть властивостей мiкрочастинок

Поява квантової механіки зумовлена необхідністю встановлення властивостей світла та законів, яким воно підкоряється. Класична фізика не могла зробити цього, бо світло має подвійну властивість:

по-перше – це хвилi з частотою 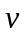та довжиною 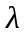, що проявляється у явищах iнтерференцiї, дифракцiї, поляризацiї та iн.;

по-друге – це частинки (корпускули) з енергiєю

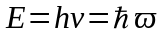(1)

та iмпульсом

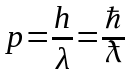, (2)

де 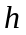– постiйна Планка, ; .

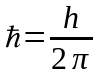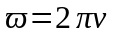Частинки свiтла – фотони, що діють у фотоелектричних явищах та iн. Сформульована у 1924 р. гiпотеза де Бройля показала, що подвiйнiсть властивостей свiтла належить iншим мiкрочастинкам – електронам, протонам та т.п. Тобто мiкрочастинцi з енергiєю Е та iмпульсом р вiдповiдає хвиля з частотою

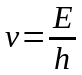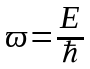або (3)

та довжиною

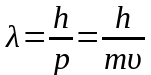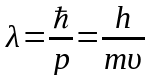або , (4)

де 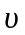– швидкiсть руху частинок; 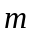– їх маса.

Цi хвилi та спiввiдношення (3) і (4) звуться iменем де Бройля.

Експериментальна перевiрка гiпотези при пропусканні через металеву фольгу пучка електронiв та рентгенiвських променiв дала однакову дифракцiйну картину, що пiдтверджує хвильові властивості електронiв. Розрахунок та з цих картин спiвпадає з (3) та (4).

Приклад практичного використання цього – електронна мiкроскопiя (оптика). Виникло запитання: володiє такими властивостями тiльки окремий електрон, чи їх система? У дослiдах Фабриканта, Бiбермана, Сушкiна (1948 р.) крiзь дифрактометр пускали слабкий пучок електронiв з iнтервалом промiж актами їх пропускання у 30000 разiв більше їхнього часу польоту у приладi, що гарантувало iзоляцiю електрона вiд впливу iнших. Вони одержали таку ж картину дифракцiї, що i у випадку дослiдiв де Бройля. Це дозволяє зробити висновок: хвильовими властивостями володiє не тільки система, але й кожний окремо узятий електрон.

1.2 Хвильове рiвняння Шредiнгера

Подвiйнiсть властивостей мiкрочастинок – рiзка вiдмiннiсть їх вiд частинок класичної фiзики. Ця якiсна вiдмiннiсть вимагає описувати їх рух за iншими законами, нiж у класичнiй фiзицi. Хвильовi властивостi показують, що їх рух пiдкоряється законам розповсюдження хвиль де Бройля. Тому хвильовi процеси описуються хвильовим рiвнянням, яке для мiкрочастинок виведено Шредiнгером. Його сенс: рух у силовому полi мікрочастинки, що володiє потенцiальною енергiєю 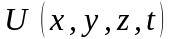, пiдкоряється хвильовому рiвнянню виду:

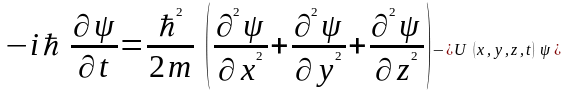. (5)

Рiшення (5) – хвильова функцiя 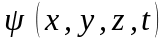. Рiвняння Шредiнгера задовольняється тiльки комплексними хвильовими функцiями. Тобто фiзичний смисл має не 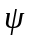, а добуток її на комплексно спряжену з нею 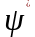. Цей добуток дiйсний та пропорцiйний iмовiрностi знаходження мiкрочастинки у момент часу t у видiленому елементi об'єму :

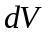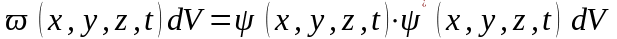. (6)

Властивостi за її фiзичним смислом:

1. Неперервна та має неперервну першу похідну.

2. Однозначна та кiнцева у всiх точках простору (тому що не може iмовiрнiсть знаходження мiкрочастинки у тому або iншому елементi мiнятися стрибкоподiбно вiд точки до точки або бути неоднозначною та нескiнченною).

Iнтеграл від (6), узятий по усьому простору 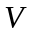, дорiвнює одиницi, тому що вiдбиває вірогідний факт – мікрочастинка є у цьому просторi:

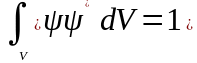. (7)

Це – умова нормiровки; функції , що складають (7), – нормованi функцiї.

Рiвняння Шредiнгера описує усю еволiцiю стану мiкрочастинки. Закон її руху визначається завданням у кожний момент часу у кожнiй точцi простору.

Амплiтудне рiвняння Шредiнгера. Потенцiйна енергiя 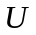у (5) – функцiя координат та часу. Але на практицi часто – функцiя координат та не залежить вiд часу. Тому запишемо повну функцію у вигляді:

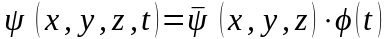. (8)

За такої умови розглянемо одновимiрний випадок, тобто рух мiкрочастинки повздовж осi 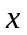. Рiвняння Шредiнгера (5) при цьому матиме вигляд:

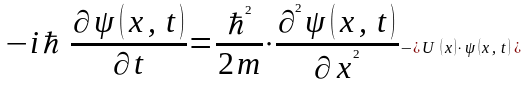. (9)

Вираз (8) стане:

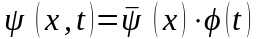. (10)

Пiдставимо (10) у (9), поділивши результат на (10), та зробимо розподіл змінних і :

.

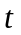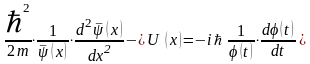Змiннi розподiленi: лiворуч – функцiя вiд x, праворуч – вiд t.

Рiвнiсть можлива помiж ними при умовi рiвностi кожної частини однiй постiйнiй величинi. Такою величиною є – повна енергiя частинки. Прирiвнюючи частини та перетворюючи рівність, одержимо:

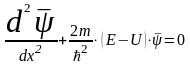, (11)

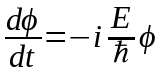. (12)

Рiвняння (11) у загальному трьохвимірному випадку буде мати вигляд:

. (13)

Сума других похiдних будь-якої функцiї – оператор Лапласа, що позначається 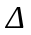. Тодi (13) буде мати вигляд:

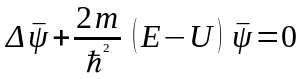. (14)

Функцiя – амплiтуда хвильової функцiї 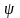, а рiвняння (11), (13) та (14) – амплітуднi рiвняння Шредiнгера (що не мiстять у собi часу).

Коли мікрочастинка рухається у обмеженому просторi, тодi рiшення рiвняння Шредiнгера вiдповiдають умовам однозначностi, кiнцевостi та неперервностi тiльки за умови суворого визначення значень 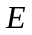: 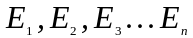, якi звуться власними значеннями енергiї мiкрочастинки. Зв'язанi з ними хвильовi функцiї 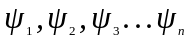, звуться власними.

Роздивимося рiвняння (12). Iнтегруючи його, одержимо рiшення для одного iз власних значень енергiї :

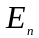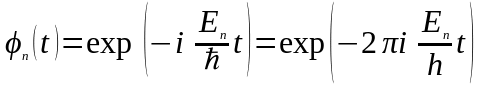. (15)

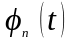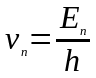показує залежнiсть повної хвильової функцiї вiд часу. Iз (15) видно, що ця залежнiсть гармонiчна з частотою або .

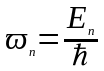Висновки

1. Якщо потенцiйна енергiя U є функцiєю тiльки координат, тодi рiшення повного рiвняння Шредiнгера має вигляд:

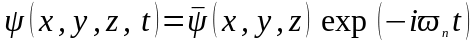. (16)

2. Iмовiрнiсть знаходження мiкрочастинки у елементi об’єму 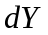у цьому випадку не залежить вiд часу та дорiвнює:

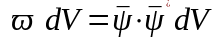. (17)

3. Розподiлення iмовiрностi у просторi є стацiонарним.

4. Стан мiкрочастинки, що вiдповiдає цим умовам, зветься стацiонарним станом. Його описує амплiтудне рiвняння Шредiнгера.