1.2 Экономический анализ полученного оптимального решения
Экономический анализ полученного оптимального решения производится с помощью отчетов по результатам, устойчивости и пределам.
Отчет 1.1 «Отчет по результатам»
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В таблице "Целевая ячейка (максимум)" приведены адрес ($I$4), исходное и результативное значение целевой ячейки. Максимальное значение целевой ячейки (максимальная прибыль предприятия) равна 793,3.
В таблице "Изменяемые ячейки" находятся данные о том, у какого АО и в каком количестве было закуплено сырьё. Изменяемые ячейки, т.е. объемы закупаемого сырья у каждого АО, принимают следующие значения: у 2-го АО закупается 11,3. У всех остальных АО сырье не закупается.
В таблице "Ограничения" показаны результаты оптимального решения для граничных условий и ограничений задачи. Указываются адреса ячеек, имя, значения – величины объемов произведенных видов продукции и количество закупок сырья, значения искомых переменных задачи.
В графе "Формула" указаны зависимости, которые были введены в диалоговом окне "Поиск решения" (система ограничений).
В графе "Значения" приведены величины объемов отдельных видов продукции и значения искомых переменных задачи.
В графе "Разница" показано количество непроизведенной продукции. [При неполном производстве продукции в графе "Статус" указывается «не связанное», а в графе "Разница" – остаток.]
В графе "Статус" указываются следующие сведения: если объем производства продукции данного типа равен максимально возможному, состояние – «связанное», при неполном производстве продукции, состояние – «не связанное».
Отчет 1.2. «Отчет по пределам»
Microsoft Excel 12.0 Отчет по пределам |
|
|
|
|
|
|
|
||
Рабочий лист: [Книга1]Отчет по пределам 2 |
|
|
|
|
|
|
|||
Отчет создан: 16.02.2012 15:01:34 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Целевое |
|
|
|
|
|
|
|
|
Ячейка |
Имя |
Значение |
|
|
|
|
|
|
|
$I$4 |
норма прибыли ЦФ-прибыль |
793,3333333 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Изменяемое |
|
|
Нижний |
Целевой |
|
Верхний |
Целевой |
|
Ячейка |
Имя |
Значение |
|
предел |
результат |
|
предел |
результат |
|
$B$2 |
сырье |
0 |
|
0 |
793,3333333 |
|
3,62674E-10 |
793,3333333 |
|
$C$2 |
сырье |
11,33333333 |
|
0 |
0 |
|
11,33333333 |
793,3333333 |
|
$D$2 |
сырье |
0 |
|
0 |
793,3333333 |
|
1,81337E-10 |
793,3333333 |
|
$E$2 |
сырье |
0 |
|
0 |
793,3333333 |
|
3,62674E-10 |
793,3333333 |
|
$F$2 |
сырье |
0 |
|
0 |
793,3333333 |
|
2,41783E-10 |
793,3333333 |
|
$G$2 |
сырье |
0 |
|
0 |
793,3333333 |
|
1,81337E-10 |
793,3333333 |
|
$H$2 |
сырье |
0 |
|
0 |
793,3333333 |
|
3,62674E-10 |
793,3333333 |
Отчет по пределам показывает, в каких пределах может измениться объем закупаемого сырья, вошедшего в оптимальное решение, при сохранении структуры оптимального решения.
Отчет 1.3. «Отчет по устойчивости»
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результ. |
Нормир. |
Целевой |
Допустимое |
Допустимое |
Имя |
значение |
стоимость |
Коэффициент |
Увеличение |
Уменьшение |
сырье |
0 |
-16,66666667 |
30 |
16,66666667 |
1E+30 |
сырье |
11,33333333 |
0 |
70 |
1E+30 |
9,999999998 |
сырье |
0 |
-28,33333333 |
65 |
28,33333333 |
1E+30 |
сырье |
0 |
-6,666666665 |
40 |
6,666666665 |
1E+30 |
сырье |
0 |
-15 |
55 |
15 |
1E+30 |
сырье |
0 |
-43,33333333 |
50 |
43,33333333 |
1E+30 |
сырье |
0 |
-21,66666667 |
25 |
21,66666667 |
1E+30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Результ. |
Теневая |
Ограничение |
Допустимое |
Допустимое |
Имя |
значение |
Цена |
Правая часть |
Увеличение |
Уменьшение |
П1 V расчетный |
1,133333333 |
0 |
2,2 |
1E+30 |
1,066666667 |
П2 V расчетный |
2,266666667 |
0 |
2,3 |
1E+30 |
0,033333333 |
П4 V расчетный |
1,7 |
466,6666667 |
1,7 |
0,025 |
1,7 |
П5 V расчетный |
1,133333333 |
0 |
4,1 |
1E+30 |
2,966666667 |
В разделе "Изменяемые ячейки" графа «Нормированная стоимость» содержит значения дополнительных двойственных переменных, показывающих, как изменится целевая функция при принудительной закупке единицы сырья у данного АО. Если значения дополнительных двойственных переменных равны 0, то основные переменные вошли в оптимальное решение.
Графа "Целевой коэффициент" показывает степень зависимости между изменяемой и целевой ячейками, т.е. коэффициенты целевой функции.
Графы "Допустимое увеличение" и "Допустимое уменьшение" показывают предельные значения приращения коэффициентов в целевой функции
,
при которых сохраняется оптимальное
решение (в каких пределах может
уменьшаться или увеличиваться норма
прибыли при закупке сырья у данных АО,
чтобы при этом сохранялась структура
закупок).
В разделе "Ограничения" в графе "Теневая цена" приведены двойственные оценки
,
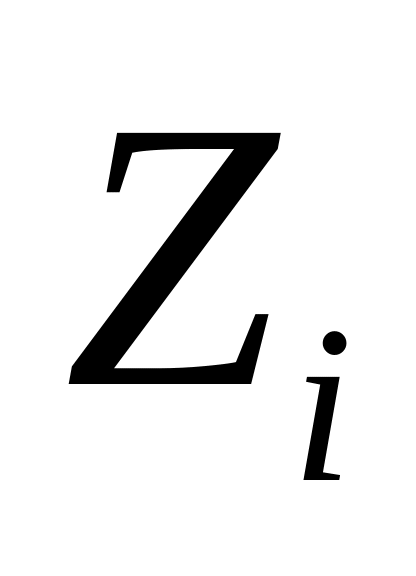которые показывают, как изменится
целевая функция (прибыль) при изменении
объема выпуска продукции на единицу.
Комментарии по первому разделу курсовой работы.
Результатом первого раздела является найденное оптимальное решение. Таким образом, филиалу предприятия выгодно закупать сырьё только у АО №2 в количестве 11,3 тонн, при этом максимум прибыли предприятия составит 11,3 тыс.рублей, и будут произведены следующие объёмы продукции: продукт 1 – 1,13 т, продукт 2 – 2,6 т, продукт 3 – 1,7т, продукт 4 – 1,13 т.
Анализируя
отчет по устойчивости, можно сделать
вывод о том, что объём выпуска продукта
4 можно увеличить на 0,025т т (допустимое
увеличение). Теневая цена этого продукта
равна 466,6
. Т.к. теневая
цена – это двойственная переменная,
показывающая изменение целевой функции
при изменении данного ресурса.
Следовательно, при увеличении объёма
выпуска продукта 4 прибыль увеличится
на (466,6*0,025)
11,665
будет равна 11,33+11,664
22,995.
Увеличивать объёмы выпуска продукции
1 ,2 и 5 нецелесообразно, т.к. прибыль от
реализации данной продукции не увеличится.
А, рассматривая столбец «допустимое уменьшение», делаем вывод, что при уменьшении объёма выпуска продукции 4 прибыль предприятия уменьшится на (466,6* 1,7) 793,22 и будет равна 11,33-793,22=509,34.