Операции над последовательностями.

1. W=U+V; то есть: W(i)=U(i)+V(i);

2. CP, W=CU; W(i)=CU(i);

Определение: последовательности U₁, …, U_m  pL(F) – базис семейства ЛРП с характеристическим многочленом F(х), если:

1. VpL(F)  c₁, …, c_m: V=c₁U₁+…+c_mU_m;

2. Константы c₁, …, c_m – определены однозначно, то есть представление 1. – однозначно.

Определение: пусть UР^, h(x)=;

 произведение последовательности U на многочлен h(x) – последовательность W=h(x)U;

Пример: x(U(0), U(1), U(2), …)=(U(1), U(2), …)

Свойства умножения последовательности на многочлен.

1. (A(x)+B(x))U=A(x)U+B(x)U;

2. (A(x)B(x))U=A(x)(B(x)U);

3. A(x)(U+V)=A(x)U+A(x)V;

Определение: характеристический многочлен наименьшей возможной степени – минимальный многочлен ЛРП: m_U(x).

Определение: импульсная последовательность с характерным многочленом f(x): e^fpL(f) – последовательность принадлежащая pL(f) с начальным вектором:

(0, ….., 0, 1)=e_m-1;

Определение: многочлен _U(x) из Т – генератор плоскости U.

Определение: аннулятор последовательности: A_nnU={g(x)P[x]g(x)U=0}.

Соотношения между семействами рекуррент.

1. pL(G)pL(F)  G(x)F(x);

2. L(G)L(F)=L((G,F));

3. L(G)+L(F)=L([G,F]);

4. (F(x),G(X))=  L(FG)=L(F)+L(G);

При этом представление каждой рекурренты из семейства l(fg) в виде суммы рекуррент из семействL(f), l(g) –однозначно. Биномиальные последовательности. Биномиальный базис.

Пусть P\0, биномиальная последовательность l-го порядка с корнем  - последовательность, знаки которой определяются по правилу: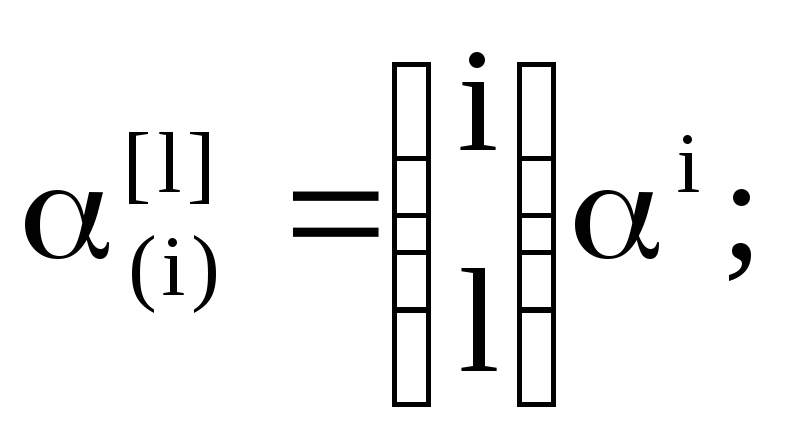

Представление лрп через функцию “след”.

Определение3: периодическая последовательность U над R^ -чисто периодическая если её предпериод =0 ((U)=0).

Определение4: периодическая последовательность U над R – вырожденная, если она имеет вид:

U=(U(0), U(1), …, U(-1), 0, 0, 0, …..).

Определение5: многочлен F(x)R[x] – периодический многочлен, если  ₀₀, tN: F(x)x^(x^t-e) (15).

T(F)- период многочлена F(x);

Наименьшее : F(x)x^(x^t-e)- обозначим через (F)- предпериод многочлена.

Определение1: UR^- периодическая, если 0, t>0: U(i++t)=U(i+), i0. (1)

Определение2: последовательность- чисто периодическая, если =0.

Определение3: вырожденная последовательность- если у неё только конечное число 1-ых знаков отлично от 0.

Утверждение1: любая периодическая последовательность- ЛРП.

Доказательство: по определению1 ,t: U(i++t)-U(i+)=0; (x^t+-x^)U=0; x^(x^t-1)U=0  UpL(x^(x^t-1);

Определение4: наименьшее натуральное t, для которого  : выполняется U(i++t)=U(i+) - период последовательности: Т(U).

Периодические многочлены.

Определение: многочлен F(x)P[x]- периодический, если  tN, >0: F(x)x^(x^t-1); (1);

Определение: наименьший min{ tN, для которого  : F(x)x^(x^t-1)}=T(F(x));

 если Т- период многочлена, то min{>0: F(x)x^(x^T(F)-1)}=(F(x));

Определение: многочлен периодический если (F)=0.

Определение: O(F)=HOK порядков корней многочлена в его поле разложения.

!!! всюду дальше: F(0)0, то есть x неF(x);

O(F)=HOK{ord_j, F(_j)=0}.

Определение: если O(F)q^m-1; degF(x)=m; F(x)- над P=GF(q), то F(x)- многочлен максимального периода.