Группы подстановок.

Будем рассматривать только конечные множества.

Опр: Пусть ; группа подстановок на множестве - это группа взаимно однозначного отображения множества в себя.

- пример. Sn – симметричная группа.

Умножение подстановок: слева направо.

;

Циклы независимы, если множество элементов не пересекается.

Опр: Транспозиция – подстановка, переставляющая только 2 элемента.

Опр: Пусть задана - число циклов длинны j в разложении подстановки g в произведения независимых циклов. - цикловая структура р.

Опр: Постановки g1, g2 – сопряженные, если

Понятие транзитивности группы подстановок.

Пусть G<Sn.

Опр: Группа подстановок G – транзитивная на множестве , если

Опр: - множество всех элементов, получаемых при действии подстановок из g на элемент - это орбита элемента .

Опр: Группа подстановок G – к-транзитивная если и существует одна подстановка (При к=1 – просто транзитивность.) Т.е. любая пара может перейти в любую – 2-транзитивность.

Примитивность группы подстановок.

Опр: Множество - блок импримитивности если для выполняется одно из условий:

1. 

2. 

Опр: Транзитивная группа G – примитивная если у нее не существует блоков импримитивности.

Опр (эквивалентное условие для определения блока импримитивности): - блок, если для

Кольцо целых чисел.

Опр: Число a делится на число b: b|a если .

Опр: Деление с остатком а на b – это представление а в виде: a=bq+r, .

Опр: Числа a,b – сравнимы по modn, если остатки от деления a,b на n совпадают. .

Обозначение: .

NOD, NOK целых чисел.

Опр: NOD целых чисел a,b(a,b)=d – натуральное число

1. d|a, d|b;

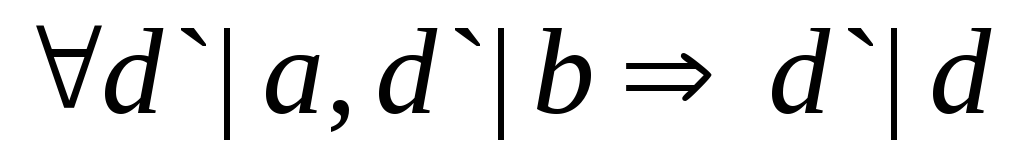2. (т.е. d – max).

Опр: NOK

1. a|D,b|D;

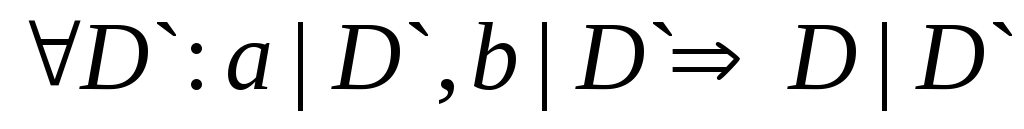2. (т.е. D – min).

Опр: a,b – взаимнопросты .

Опр: – простое – если оно делится только на 1 и само на себя.

Опр: b – собственный делитель а, если b|a, 1<b<|a|. Другими словами р – простое, если оно не имеет собственных делителей.

Опр: Представление целого числа n в виде произведения степеней попарно различных простых чисел – каноническое разложение числа n.

Кольцо вычетов целых чисел.

- конгруэнция на Z. Пусть [a]n – класс эквивалентных элементов относительно ; а остатков: - разные классы.

- множество + операции: . В силу теоремы, что - конгруэнция, введенные операции – введены корректно. - это множество с этими операциями – это кольцо из n элементов.

Для простоты: - наименьший неотрицательный элемент из класса [a] .

Идеалы колец.

Опр: Пусть - кольцо - идеал кольца R, если .

Пример: R=Z, J – четные числа .

Рассматриваем свойства коммутативных колец.

Опр: Идеал I – максимальный идеал, если из условия, что либо J=R.

Опр: Пусть - сравнение по модулю идеала I:

Идеалы кольца целых чисел.

Теорема: Все идеалы кольца целых чисел исчерпываются множествами вида: .

Теорема: .

Решение сравнения в кольце целых чисел Zn.

Пусть - обозначение. Дано: Zn; [a][x]=[b]; ; Пусть - сравнение по модулю n, здесь решений бесконечное множество т.к. в Zn.

Теорема:

1. В Zn сравнение: 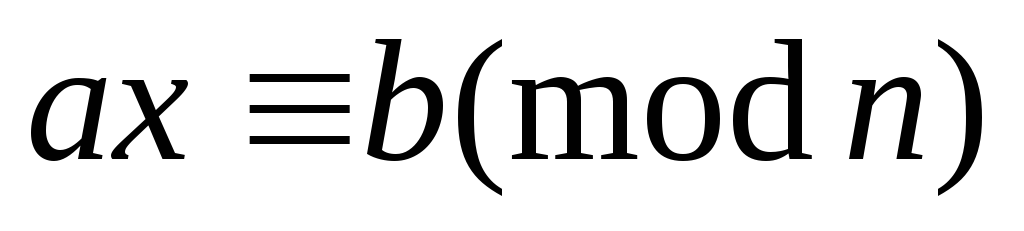имеет решение (a,n)|b

2. Если (a,n)|b, то сравнение имеет (a,n)=d различных по модулю n решений вида: 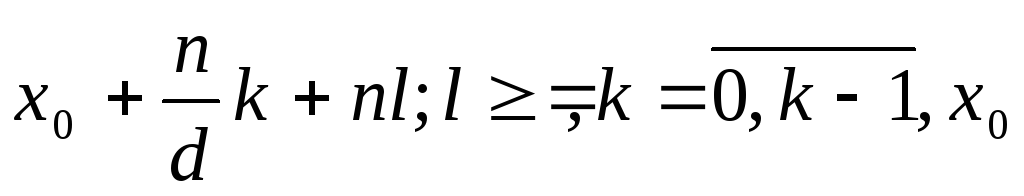- некоторое фиксированное решение.

Пример1:

1. (a,6)=1 Пусть a=5;

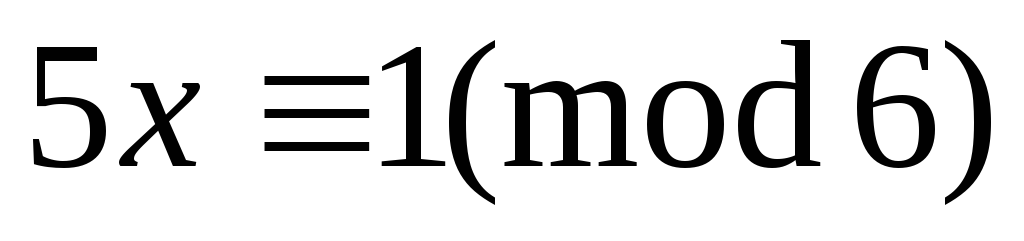
2. 5U+6V=1; U=-1

3. 

4. 

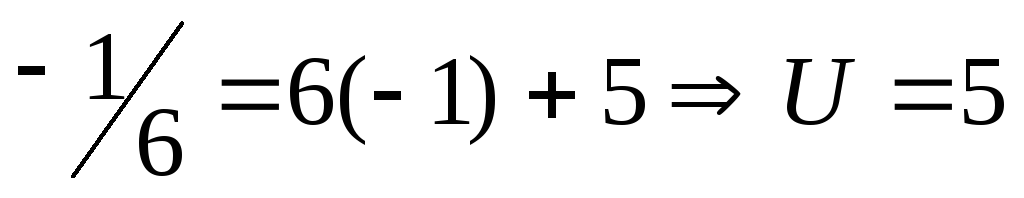
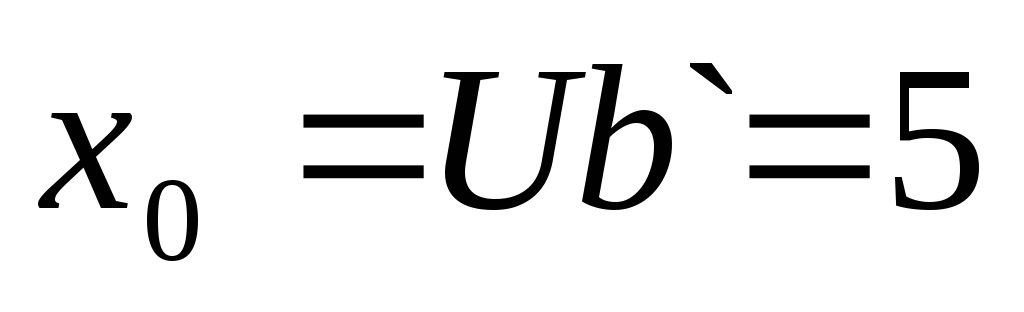
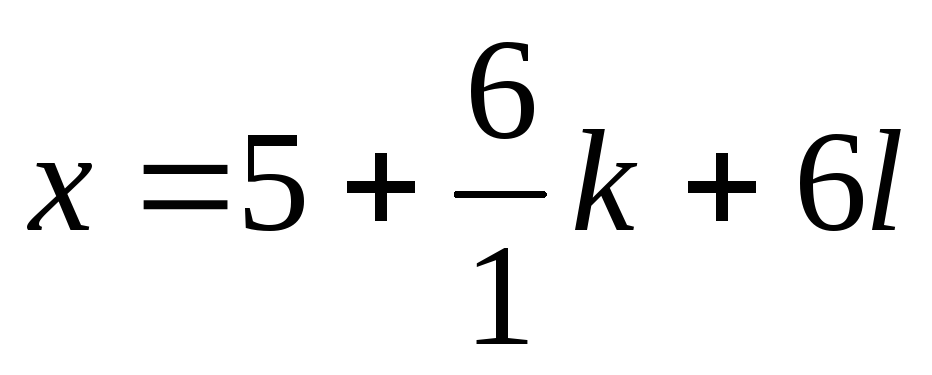
Пример2: . Найти обратный к элементу [4]?

нет решений. Пусть есть решение.

Пусть

Конечные поля.

Простейшие свойства полей: Р – поле – это коммутативное К с е, в котором каждый ненулевой элемент обратим. .

Свойства:

1. (P,+) – коммутативная группа G

   1. 

   2. 

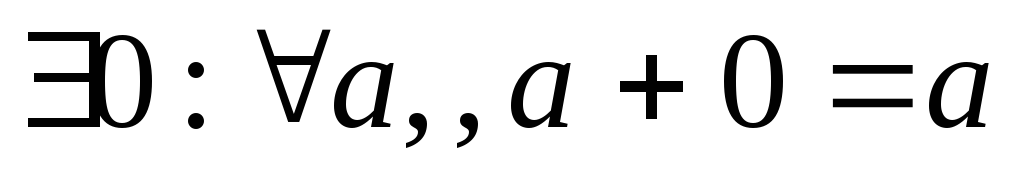
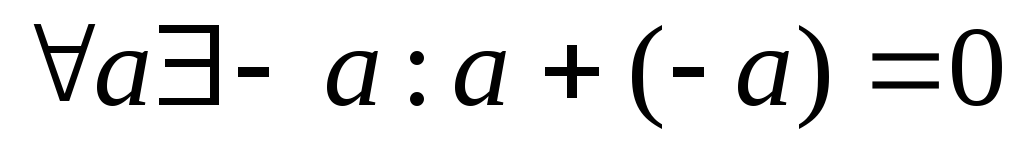
   3. a+b=b+a

   4. 

   5. 

2. 

   2. 

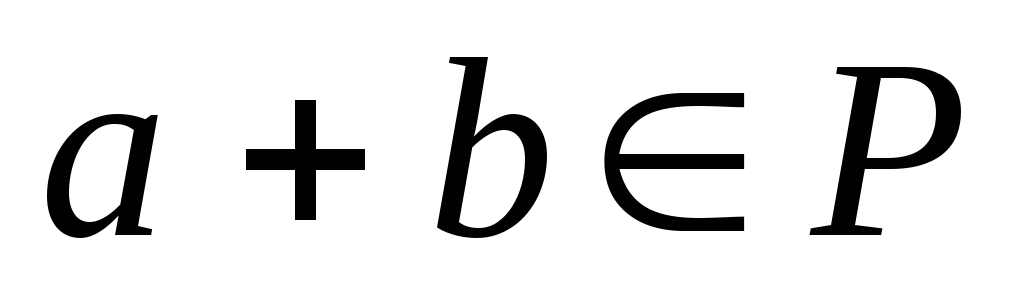
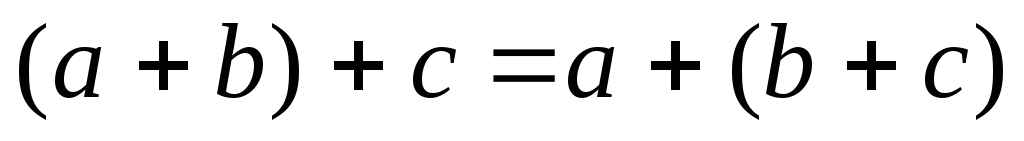
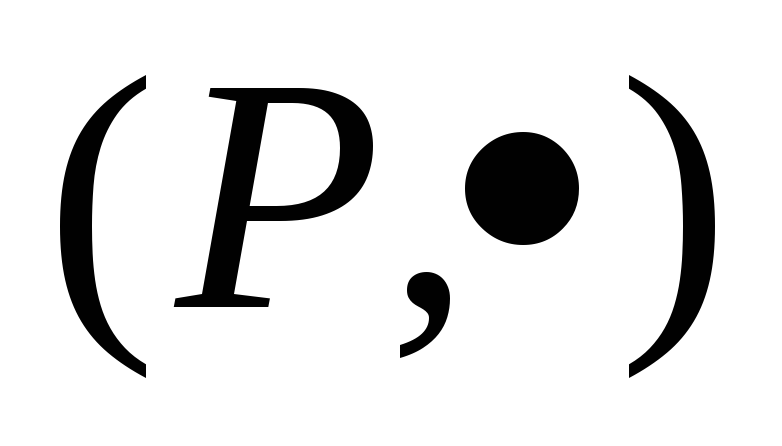
3. т.к. К – коммутативно значит ab=ba

4. 

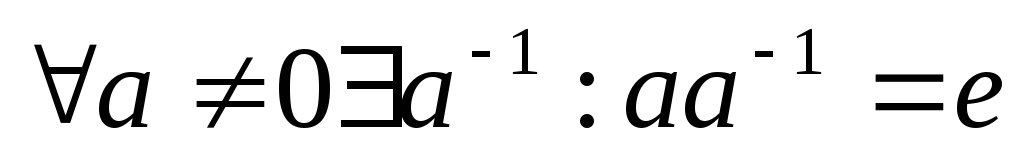
Пример1: рациональные действия, комплексные числа – поля.

Пример2: GF(2) – поле Галуа (конечное поле)

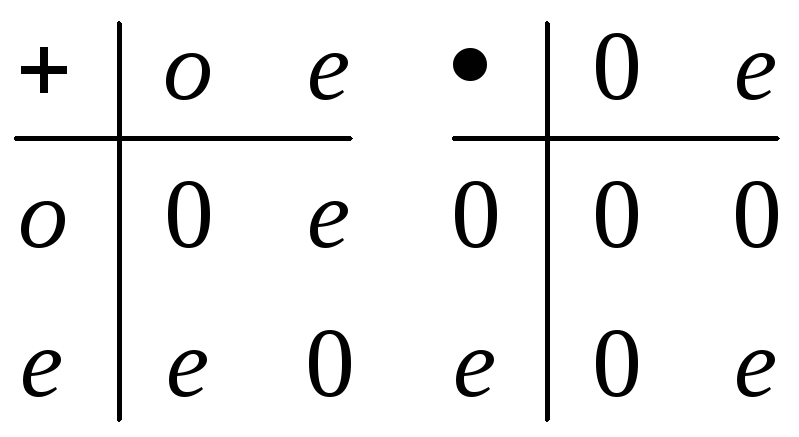- такое множество элементов {0,e} – поле.

Пример3: Zp (если р – простое) – поле.

Пример4: - множество таких чисел образует поле. Оно больше Q, но меньше поля R.

Опр: Характеристика поля Р – минимальное натуральное число р. . Если такого р не существует, по определению полагают р=0.

Пример5: GF(2), т.к. e+e=0, т.е. 2e=0, a .

Пример6: R .

Пусть Р – конечное поле. Построим последовательность: e,2e,3e,…,ne, т.к. в поле конечное число элементов значит где-то есть повторения: (Пусть k>j)

Пусть ke=je; (k-j)e=0. (k-j) – какое-то натуральное число, пусть не min, т.е. это верхняя граница значит есть min. Значит если Р – конечно, то , т.е. конечное поле имеет конечную характеристику.

Замечание: Обратное не верно, существуют бесконечные поля, имеющие конечную характеристику.

Опр.: Поле называется простым, если оно не содержит собственных подполей, т.е. если Q<P значит Q=P(более простых полей, чем Р в нем нет).

Опр.: В конечном поле элемент с таким свойством называется примитивным

Т.е. в конечном поле существует примитивный элемент, где 0, ¹, ², …,^|P|-1 – все различные элементы поля Р

{В абелевой группе существует : ord=expG}

expG=min{t : G, ^t=e}