Кольцо многочленов над полем

Пусть Р – поле;

Обозначим: Р - множество носителей с элементами из Р; (а₀ а₁ а₂ … ), а_jР

Р : если (а₀ … а_n …), то k : а_j=0, для jk, т.е. начиная с какого-то номера они все нули.

Определим на множестве : +=, c_k=a_k+b_k

×=, c_k=a_jb_k-j

Опр.: Будем говорить, что многочлен a(x) делит b(x), т.е. a(x)½b(x), если существует с(х) : a(x)× c(x)=b(x)

Опр.: Степень многочлена a(x) – deg a(x) – номер наибольшего ненулевого коэффициента в представлении: a(x)=a_jx^j.

Если а(х)=0, то полагаем deg a(x)= -

(примечание: пусть a(x)=a₀0 тогда deg a(x)=0).

Опр.: Разделить a(x) на b(x) с остатком – значит, что b(x) можно представить в виде b(x)=q(x)a(x)+r(x), deg r(x)<deg a(x)

Опр.: NOD многочленов a(x), b(x) – многочлен d(x):

1) d(x)|a(x); d(x)|b(x)

2) d'(x)|a(x), d'(x)|b(x) следовательно d'(x)|d(x)

Замечание: для определенности считаем, что старший коэффициент многочлена равен 1.

Опр.: Многочлены a(x) и b(x) называются взаимнопростыми, если их NOD = 1.

Опр.: a(x) – собственный делитель b(x), если d(x)|b(x) и 0<deg a(x)<deg b(x), т.е. a(x)const.

Опр.: Многочлен a(x) – неприводимый, – если он не имеет собственных делителей, иначе – приводимый.

Замечание: неприводимый многочлен делится либо на константу, либо на самого себя.

Свойства взааимнопростых многочленов

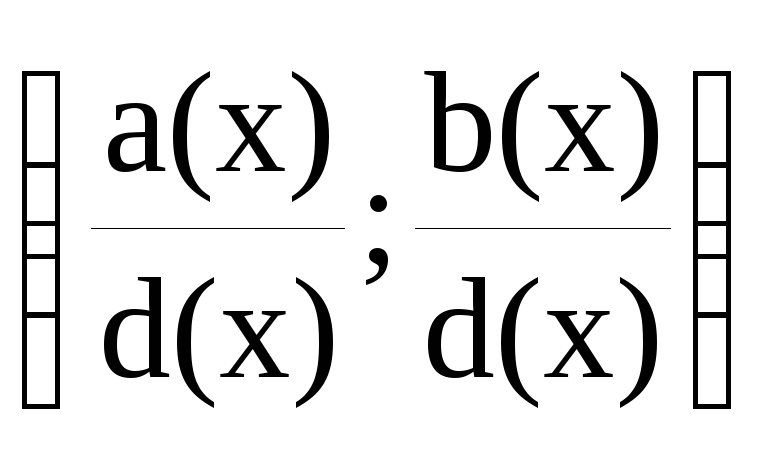1. (a(x),b(x))=d(x) =1

Доказательство: существуют многочлены u(x), v(x) : u(x)a(x)+b(x)v(x)=d(x)

u(x) + v(x) = 1

первое свойство доказано

2. (a(x),b(x))=1; a(x)|c(x), b(x)|c(x) следовательно a(x)b(x)|c(x)

Доказательство: u(x)a(x)+v(x)b(x)=1;

c(x)=a(x)q(x)

u(x)a(x)q(x)+v(x)b(x)q(x)=q(x)

следовательно b(x)|q(x)

значит q(x)=b(x)q₁(x) следовательно c(x)=a(x)b(x)q₁(x). ч.т.д.

3. (a(x),b(x))=1, a(x)|c(x)^.b(x) следовательно a(x)|c(x)

Доказательство: u(x)a(x)+v(x)b(x)=1; |c(x)

u(x)a(x)c(x)+v(x)b(x)c(x)=c(x)

следовательно a(x)|c(x). ч.т.д.

4. (a(x),b(x))=1, (a(x),c(x))=1 следовательно (a(x),b(x)^.c(x))=1

Доказательство: [u(x)a(x)+v(x)b(x)=1][m(x)a(x)+l(x)c(x)=1]

a(x)(u(x)a(x)m(x) + u(x)c(x)l(x) + m(x)b(x)v(x)) + b(x)c(x)v(x)l(x) = 1,

где u'= u(x)a(x)m(x)+u(x)c(x)l(x)+m(x)b(x)v(x), v'=v(x)l(x). ч.т.д.

Опр.: NOK многочленов a(x), b(x) - [a(x),b(x)] называется многочлен D(x) со свойствами:

1. a(x)|D(x); b(x)|D(x)

2. для любого D'(x) : a(x)|D'(x), b(x)|D'(x) следует D(x)|D'(x)

Свойства неприводимых многочленов

1. Везде старший коэффициент равен 1.

Теорема: пусть f(x) – неприводимый многочлен. Тогда для любого многочлена g(x) выполнено либо f(x)|g(x), либо (f(x),g(x))=1

Доказательство:

1. Если (f(x),g(x))=1 то свойство справедливо

2. пусть (f(x),g(x))=d(x), deg d(x)>0 значит f(x)|g(x) – докажем это:

d(x)|f(x) и deg d(x)>0, т.е. d(x)0 следовательно

d(x)=f(x), т.к. f(x) – неприводимый многочлен, а т.к. d(x)|g(x) значит f(x)|g(x)

2. пусть f(x) – неприводимый многочлен. Если неприводимый многочлен делит произведение двух других многочленов, т.е. f(x)|a(x)^.b(x), то либо f(x)|a(x), либо f(x)|b(x).

Доказательство: пусть f(x)†a(x) значит f(x)|b(x) – докажем это:

из свойства 1. неприводимых многочленов следует:

(f(x),a(x))=1 + f(x)|a(x)^.b(x)

откуда получаем, что f(x)|b(x) – по 3. свойству взаимопростых многочленов.

ч.т.д.

Опр.: Представление произвольного многочлена a(x) в виде:

a(x)=a_nj(x)^kj,

где f₁(x),…,f_r(x) – попарно различные неприводимые многочлены со старшим коэффициентом равным 1, k_j>0 – есть каноническое разложение многочлена a(x); deg a(x)=n.