Свойство сравнимости в кольце многочленов над полем

Пусть P(x) – кольцо многочленов над полем Р

Опр.: a(x) = b(x) (mod f(x)) – сравнимы по модулю многочлена f(x), если остатки от деления совпадают:

a(x)=f(x)q₁(x)+r₁(x) и b(x)=f(x)q₂(x)+r₂(x) r₁=r₂

Опр.: Множество многочленов a₁(x), a₂(x),…,a_t(x) – полная система представителей классов эквивалентностити относительно отношения º(mod f(x)) если:

1. для любого j¹k a_j(x) не сравним с a_k(x)(mod f(x))

2. для люього b(x)P[x] существует k : b(x)=a_k(x) (mod f(x)).

Корни многочленов над конечным полем и их свойства

Пусть a(x)=

Опр.: - значение многочлена a(x) (x)_ние много из поля.

Опр.: Если для некоторого многочлена a(x) над полем Р и элемента ? из Р выполнено условие a(α)=0,

Опр.: Кратность корня – наибольшее значение r : r=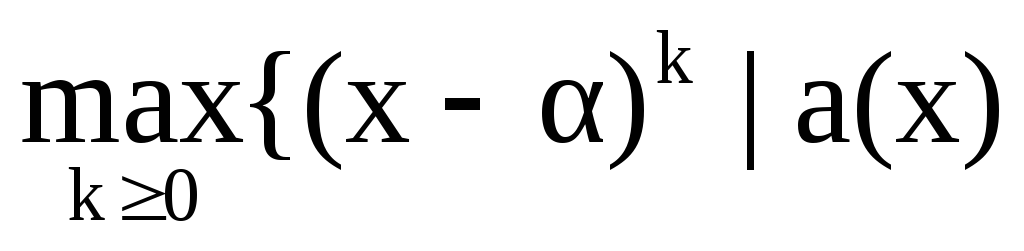α

Неприводимые многочлены над числовым полем с, полем действительных чисел r и полем рациональных чисел z

Теорема (Гаусса): Любой многочлен над полем С имеет в этом поле корень.

Следствие: Над полем С неприводимы многочлены только первой степени.

Опр.: Многочлен a(x) над кольцом Z (с целыми коэффициентами) – примитивный, если множество его коэффициентов взаимно просто в совокупности.

Опр.: Два числа взаимно просты, если для любого простого числа одно из них на него не делится.

Опр.: Множество (a₀,…,a_n) – взаимно просто в совокупности, если для p – простого k, 0kn : p|a_k

Пример: (6,10,15)=1, т.е. NOD совокупности равен 1.

Опр.: Многочлены a(x), b(x) над полем Q – ассоциированные, если : a(x)=c^.b(x).

Опр.: Пусть Р – поле следовательно множество Q P – подполе Р, если Q P и Q – поле.

Пример: Q < R < C

Опр.: Поле называется простым, если оно не содержит собственных подполей, т.е. если Q<P значит Q=P(более простых полей, чем Р в нем нет).

Опр.: В конечном поле элемент с таким свойством называется примитивным

Т.е. в конечном поле существует примитивный элемент, где 0, ¹, ², …,^|P|-1 – все различные элементы поля Р

{В абелевой группе существует : ord=expG}

expG=min{t : G, ^t=e}

Определение: элемент порядок которого равен мощности поля без единицы называется примитивным элементом поля:

Определение: пусть Q>P; унитарный многочлен f(x) наименьшей степени с коэффициентами из Р , такой что для  Q, f()=0 – минимальный многочлен элемента  над полем Р: m_,P(x);

Отображение “след”.

Определение: пусть есть поле Р из q элементов и поле Р^/ из q^m элементов. Отображение называется “следом” если:

Линейные рекуррентные последовательности.

Последовательность над полем Р – произвольное отображение множества N₀ в поле Р:

U: N₀P; U=(H(0), U(1), U(2), …);

P^ - всё множество последовательностей над Р.

Линейная рекуррентная последовательность (ЛРП) над Р – последовательность U для которой  m, c₀, c₁, …, c_m-1P:  i 0 :

Отрезок последовательности: (U(c), …, U(m-1)) – начальный вектор рекуррентна.

Определение: - характеристический многочлен последовательности.

Порядок рекуррентны = deg(F(x));

Пример1: ГПр – ЛРП: b_n+1=qb_n; F(x)=x-q;

Пример2: АПр  а_n+1=a_n+d=a_n+(a_n-a_n-1);  a_n+2=2a_n+1-a_n; F(x)=x²-2x+1=(x-1)²;

Пример3: Фибоначчи: U_n+2=U_n+1+U_n; 1,1,2,3,5,8,11,…; F(x)=x²-x-1;

Утверждение: ЛРП U с характеристическим многочленом F(x), degF(x)=m – однозначно определяется своим начальным вектором длины m.

Обозначение: множество всех ЛРП над Р с характеристическим многочленом F(x): pL(F).