Элементы теории множеств.

Бинарное отношение на множестве Х – любое подмножество декартового квадрата множества Х. .

Декартово произведение множеств: , для n множеств .

Если то ~ .

Свойства бинарного отношения:

1. Рефлексивность:

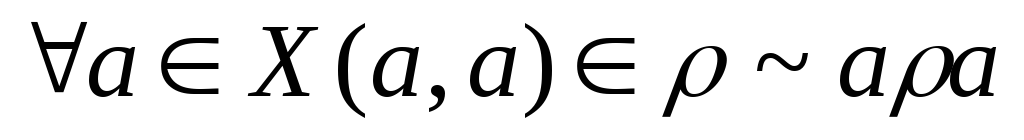
2. Симметричность:

3. Транзитивность:

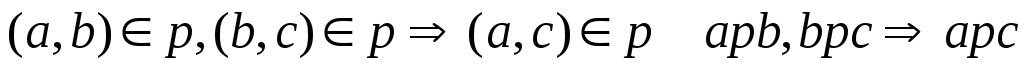
4. Ассимитричность:

Отношение эквивалентности: если оно рефлексивно, симметрично, транзитивно.

Отношение порядка: если оно рефлексивно, транзитивно, ассимитрично.

(Строгого порядка – если 3.)

Пример 1: отношение равенства – отношение эквивалентности.

Пример 2: Множество действительных чисел с оператором - отношение порядка.

1. 

2. 

3. 

Пример 3: R с < - выполняется только 3.

Пример 4: Выполняется 3, 4 и не выполняется 1, 2.

X={1,2,3}; p={(1,2),(2,3),(1,3)}

4 выполняется автоматически, так как нет пар (a,b),(b,a).

Опр: Пусть р – отношение эквивалентности на Х, тогда множество элементов - класс эквивалентных элементов для элемента а по отношению р.

Основные алгебраические структуры.

Опр: Отображение множества Х в множество Y – закон по которому каждому ставится в соответствие некоторый .

Заметим, что бинарное отношение .

Свойства отображений:

1. Сюръективность.

2. Инъективность.

3. Биективность.

Опр: Бинарная операция на множестве Х – отображение декартового квадрата множества Х в себя:

Свойства операций:

1. Коммутативность (обозначим +): , если .

2. Ассоциативность (*):

3. Дистрибутивность (*,0):

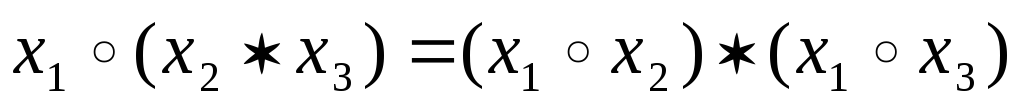
Опр: Множество Х с бинарной операцией * - полугруппа (Хб*)

• Пример (N,)

Опр: Пусть (Х,*) – полугруппа, элемент е-еденичный, если

Опр: Для элемент - обратный, если

Опр: Полугруппа (Х,*) – группа, если существует е относительно * и для каждого

Пример: (Z,+)

Опр: Пусть на множестве Х введены две операции: (Х,+,0) – множество Х с двумя бинарными операциями – кольцо, если:

1. (Х,+) – абелева группа.

2. - дистрибутивно относительно +.

Пример: (Z,+,) – множество квадратных матриц (nxn) над полем Z.

Опр: Поле – коммутативное кольцо с е, в котором каждый ненулевой элемент имеет обратный по умолчанию.

Опр: Гомоморфизм – группы - такое отображение множества G в K, при котором . Если - биективное отображение GK, то - изоморфизм группы и гомоморфизм колец

1. 

2. 

Опр: Конгруэнция на множестве Х с операцией * - (Х,*) – отношение эквивалентности р на Х со свойствами: . Говорят, что отношение р согласовано с операцией *.

Элементы теории групп.

Опр: Пусть - группа: е – определен однозначно и - однозначен.

Опр: Пусть - группа, тогда Н – подгруппа группы G, если:

1. 

2. - сама группа.

Свойства отображений конечных множеств.

Пусть - множество, .

Опр: Пусть - отображения - композиция если т.е. ; т.е.

Произведение отображений: - полугруппа.

Свойства подгрупп.

Опр: Мощность (порядок) группы – число ее элементов.

Опр: Пусть задана (G, ), подгруппа, порожденная множеством М: т.е. объединения всех подгрупп, содержащих М как подмножество. (т.е. самая маленькая подгруппа, содержащая М).

Опр: Пусть порядок элемента : где . - d элементов => все различны. =>

Опр: Экспонента группы – наименьшее натуральное число: