§9. Теорема Пуассона (для редких событий).
Пусть
в серии из n
независимых испытаний вероятность
появления события А в любом испытании
,
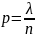тогда вероятность появления события А
в этой серии опытов ровно m
раз при достаточно большом n
(n
стремится к бесконечности) выражается
приближенной формулой Пуассона:
.
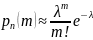В этой формуле λ = n*p; m=0, 1, 2,…
Формулу применяют, когда р крайне мала, т.е. появление события А – редкое событие, а количество n – достаточно велико.
Формулу Пуассона можно считать математической моделью простейшего потока событий.
Определение. Потоком событий называют последовательность событий, наступающую в случайные моменты времени.
Определение. Поток событий обладающий свойствами стационарности, ординарности и отсутствия последствий, называется простейшим, или пуассоновским потоком событий.
Свойство стационарности означает, что вероятность появления n событий на участке времени длины τ зависит только от его длины и не зависит от начала отсчета.
Среднее число событий, появляющихся в единицу времени называют интенсивностью потока и обозначают λ(t).
Интенсивность λ = cos(t).
Определение. Ординарность означает что события появляются не группами, а по одиночке, т.е. вероятность появления больше одного события за малый участок времени считается невозможным.
Определение. Свойство отсутствия последствия означает, что вероятность появления k событий на любом участке времени длины τ не зависит от того, сколько событий появилось на любом другом, не пересекающимся с ним участком.
Формула Пуассона для простейшего события имеет вид:
.
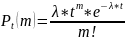Пример 1: Среднее число вызовов, поступивших на телефон за одну минуту = 2. Найти вероятность того, что за 4 минуты поступит:
4 вызова
Менее 4 вызовов
Не менее 4 вызовов
Решение:
=
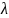2 t = 4
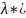t
= 8
;
Задание: 1) В здании 1000 лампочек. Вероятность выхода из строя одной лампочки в течение года p =0.003. Найти вероятность того, что в течение одного года выйдет из строя более трех ламп.
2) Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,004. Найти вероятность того, что в пути повреждено меньше трех изделий.
Упражнения для самостоятельной работы.
Сколькими способами можно выбрать 3 дежурных из группы в 20 человек?
На склад поступило 35 холодильников. Известно, что 5 холодильников с дефектами, но неизвестно, какие это холодильники. Найти вероятность того, что два взятых наугад холодильника будут с дефектами.
По каналу связи может быть передана одна из трёх последовательностей букв: АААА, ВВВВ, CCCC, причём априорные вероятности каждой из последовательностей равны: 0,3; 0,4; 0,3 ; соответственно. Известно, что действие шумов на приёмное устройство уменьшает вероятность правильного приёма каждой из переданных букв до 0,6, а вероятность приёма переданной буквы за две другие, увеличивается до 0,2 и 0,2. Предполагается, что буквы искажаются независимо друг от друга. Найти вероятность того, что была передана последовательность АААА, если на приёмном устройстве получена последовательность АВСА.
В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.
Сколько следует сыграть партий в шахматы с вероятностью победы в одной партии, равной 1/3, чтобы наивероятнейшее число побед было равно 5?
В жилом доме имеется 6400 ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что число одновременно включенных ламп будет между 3120 и 3200. Найти наивероятнейшее число включенных ламп среди 6400 и его соответствующую вероятность.
В пути повреждается в среднем каждое десятое изделие. Определите вероятность того, что в партии из 500 изделий поврежденных окажется от 50 до 70 изделий.
Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит более двух разбитых бутылок.