§3. Статистическое и геометрическое определение вероятности. Статистическое определение вероятности.

Пусть произведена серия из n опытов, в каждом из которых событие А может появиться или не появиться. В m опытах это событие появилось.

Определение. Частотой события А называется отношение числа опытов, в которых событие А появилось, к общему числу опытов w(A)

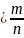
При небольшом числе опытов частота носит случайный характер и может заметно меняться от одной группе опытов к другой.

Однако частота обладает свойством устойчивости, т.е. по мере увеличения числа опытов частоты мало отличаются друг от друга и группируются около некоторого постоянного числа P(A) – вероятности события А.

Закономерности, в которых проявляются свойства устойчивости, называются статическими. Частота – статическая вероятность.

Свойства статической вероятности:

1. 0≤w(A) ≤1;

2. w(Ω)=1;

3. w(Ø)=0;

4. w(A+B) = w(A) + w(B), где A,B – несовместны и не зависят друг от друга.

Геометрическое определение вероятности

Применяется, когда исходы опыта равновозможные, а пространство элементарных событий бесконечно.

Н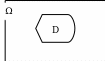 а плоскости рассмотрим некоторую область Ω, S (Ω) – площадь Ω, S(D) – площадь области.

В области Ω случайно выбирается точка Х. Говорят: “бросить току Х в область Ω”.

При этом попадание Х в Ω - событие достоверное. Считают, что вероятность попадания в D пропорциональна S(D) и не зависит от её расположения и формы.

Определение. Геометрической вероятностью события А называется отношение .

Р(А) = .

Р(А) = 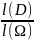= = 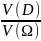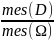, где mes – мера измерения (длина, объём,..).

Свойства аналогичны свойствам геометрической вероятности.

Задание: 1) Два человека договариваются о встрече на заданном промежутке времени t. Пришедший первым ожидает в течение времени l<t. Какова вероятность встречи?

2) Двое лиц договариваются о встрече на следующих условиях: каждый из них приходит к указанному месту независимо друг от друга в любой момент времени от двенадцати до часу и ждет другого в течение 20 минут, после чего уходит. Какова вероятность того, что встреча состоится?

§4. Теоремы сложения и умножения вероятностей. Теорема сложения вероятностей

Теорема: вероятность суммы конечного числа попарно несовместных событий равна сумме вероятностей этих событий.

Р(А₁+А₂+…+А_n) = P(A₁)+P(A₂)+…+P(A_n), A_i·A_k ≠ Ø, i≠k.

Следствия:

1. Если события А₁,А₂,…,А_n образуют полную группу несовместных событий, то сумма их вероятностей равна единице, т. к. то, что произойдёт одно из них – это событий достоверное.

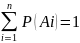
2. Сумма вероятностей противоположных событий равна единице.

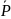(А+А) = Р(Ω) = 1.

3. Будем говорить, что событие А влечёт за собой событие В, если всякий раз, когда происходит событие А, обязательно происходит событие В. Обозначают: А→B

Если А→B, то Р(В-А) = Р(В)-Р(А).

Теорема сложения вероятностей для произвольных событий

Пусть А и В – произвольные события (совместные или несовместные). Вычислим сумму Р(А+В).

Из геометрического анализа действий над событиями следует, что А+В = А – АВ +В, где (А-АВ) и В – события несовместные.

Р(А+В) = Р(А – АВ) + Р(В) по теореме сложения вероятностей.

По следствию АВ→А, следовательно, Р(А)-Р(АВ), т. е.

Р(А+В) = Р(А – АВ) + Р(В) = Р(А) + Р(В) – Р(АВ).

Теорема: для произвольного числа событий вероятность их суммы равна сумме вероятностей событий без вероятности их совместного появления.

Для случая трёх слагаемых:

Р(А+В+С) = Р(А)+Р(В)+Р(С)-Р(АВ)-Р(АС)-Р(ВС).