Часть 1. Предмет теории вероятностей. Случайные события и их классификация. Классическое определение вероятности. Действия над событиями и элементы комбинаторики.

§1. Предмет теории вероятностей и основные определения

Определение. Теория вероятностей – математическая наука, изучающая закономерности случайных явлений. При научном исследовании различных явлений природы часто приходится встречаться с явлениями, которые при многократном повторении каждый раз протекают несколько по-иному. Такие явления называются случайными.

Попытки математики изучать случайные явления делались ещё в Древней Греции, Риме, Китае. Но начало теории вероятностей положила переписка Паскаля и Ферма, в которой они в 17 веке излагали начала и основы теории вероятностей.

В 18 веке основной интерес представляли случайные события. В 19 веке стали изучать случайные величины (Муавр, Бернулли, Лаплас, Гаусс, Пуассон). Их работы относятся к теории ошибок наблюдений. Чёткий логический смысл понятие случайной величины приобрёло в работах академика Колмогорова. Во 2-й четверти 20-го века под влиянием физики, биологии и инженерного дела в теории вероятностей начинают изучаться случайные процессы. Их определение связано с именами Колмогорова, Хингина, Слуцкого. Предшественниками их были Лаплас, Пуанкаре и Марков. Сейчас теория вероятности развивается как математическая статистика и случайные процессы.

Основные понятия теории вероятностей

Определение. Событием называется всякий факт, который в результате опыта может произойти или не произойти. Иначе: всякий возможный исход события.

Обозначение: А, В, С,…

Примеры событий:

1. Появление герба при бросании монеты;

2. Попадание в цель при выстреле;

3. Появление туза при вынимании карты из колоды.

Классификация событий:

События классифицируют по возможности появления и по характеру взаимосвязи.

Определение. Событие называется достоверным Ω, если в результате опыта оно произойдёт непременно.

Примеры достоверных событий:

1. Появление белого шара из ящика, в котором все шары белые;

2. Выпадение не более 6 очков при бросании игральной кости.

Определение. Событие называется невозможным Ø, если оно в данном опыте не может произойти.

Примеры невозможных событий:

1. Появление чёрного шара из ящика, в котором все шары белые;

2. Выпадение 7 очков при бросании игральной кости.

Пусть А – некоторое событие. Под событием, противоположным событию А (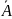 ), понимают событие, состоящее в том, что А не произойдёт.

Пример: А стрелок попал в мишень, – не попал.

События А и В называют несовместными, если они никогда не происходят одновременно в данном опыте.

Два или несколько событий называют равновозможными, если условия их появления одинаковы и нет оснований утверждать, что какой-либо из них в результате опыта имеет больше шансов появиться, чем другое.

Пример: при бросании игральной кости выпадение любого количества очков от 1 до 6 – равновозможные события.

Несколько событий А₁, А₂ ,…, А_n образуют полную группу событий, если в результате опыта обязательно должно появится хотя бы одно из них. Эти события попарно несовместны.

Примеры:

1. При выстреле в мишень – попадание и промах;

2. Появление любой карты из колоды.

Группы событий, которые обладают всеми тремя свойствами (попарно несовместны, равновозможные и образуют полную группу) называются случаями или шансами.