4.1. Момент силы

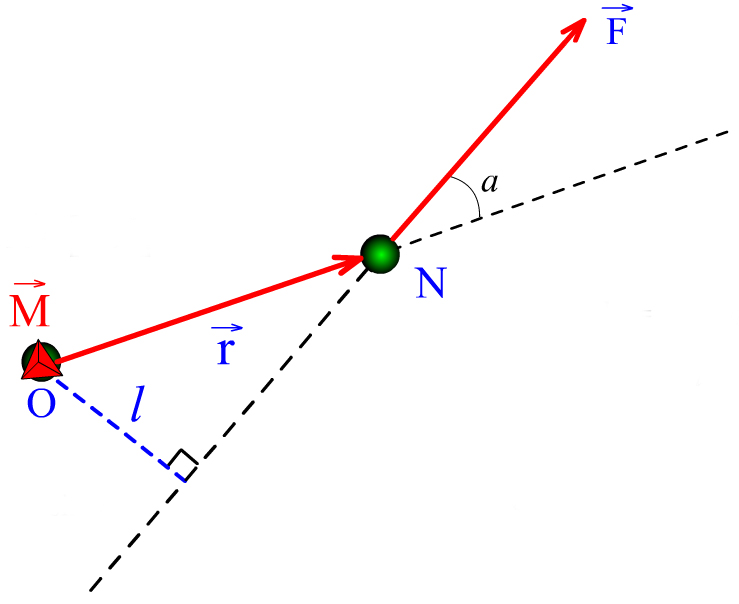
Для приведения тела во вращение необходимо, чтобы приложенная к нему сила создавала момент. Моментом силы относительно неподвижной точки (рис.4.2) называется вектор , (1.4.1)

Рис.4.2

где - радиус-вектор точки приложения силы.

Вектор проходит через точку . Он перпендикулярен плоскости рисунка и направлен «к нам». Модуль момента силы определяется выражением:

(1.4.2)

где - плечо силы (длина перпендикуляра, опущенного из точки на линию действия силы).

При вращении тела вокруг неподвижной оси вращательный момент создает только одна составляющая действующей на него силы, а именно - касательная к траектории точки ее приложения. Следовательно, вектор момента силы относительно начала координат равен (1.4.3)

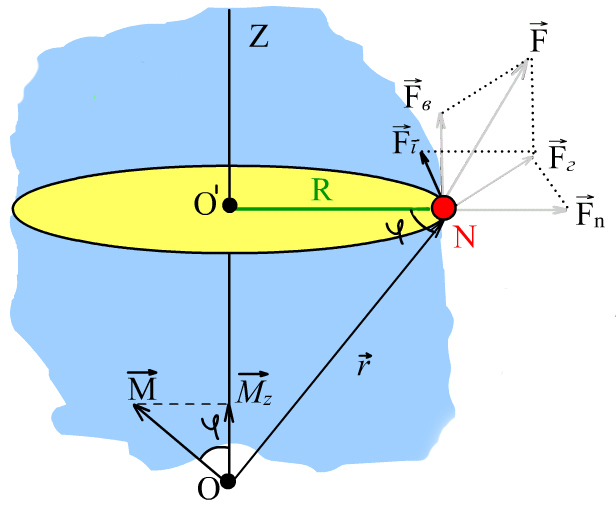
Рис.4.3

Направление вектора указано на рисунке. Его модуль равен: . (1.4.4) Вектор момента силы относительно оси (рис.4.2) представляет собой проекцию на эту ось вектора . Он направлен вдоль оси , не имеет определенной точки приложения, его модуль равен (1.4.5)

где – расстояние от оси до линии действия силы .

4.2. Момент инерции тела

Момент инерции тела – величина, определяющая его инертность во вращательном движении.

В динамике поступательного движения инерцию тела полностью характеризует его масса. Влияние собственных свойств тела на динамику вращательного движения оказывается более сложным, чем при поступательном движении.

Момент инерции материальной точки относительно оси вращения равен произведению массы точки на квадрат расстояния от точки до этой оси:

. (1.4.6)

Момент инерции тела относительно оси вращения равен сумме моментов инерции всех его материальных точек относительно этой оси:

. (1.4.7)

Следовательно, на инертность тела во вращательном движении влияют форма и геометрические размеры тела, его расположение относительно оси вращения, особенности распределения массы по объему.

В табл. 4.1 приведены моменты инерции некоторых тел правильной геометрической формы, выполненных из однородных материалов:

Таблица 4.1

Тело	Положение оси вращения	Момент инерции
Полый тонкостенный цилиндр радиуса	Ось симметрии
Сплошной цилиндр или диск радиуса	Ось симметрии
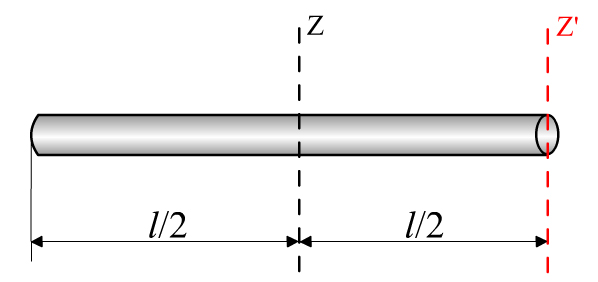
Прямой тонкий стержень длиной	Ось проходит через середину стержня перпендикулярно ему
Шар радиусом	Ось симметрии

Для расчета момента инерции тела относительно произвольной оси, не проходящей через центр масс, применяют теорему Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс, параллельно данной оси, и произведения массы тела на квадрат расстояния между этими осями: . (1.4.8)

Рис.4.4

Например, момент инерции однородного тонкого стержня (рис.4.4)длиной и массой относительно оси , перпендикулярной стержню и проходящей через его конец равен:

При переносе оси вращения из центра масс в конец стержня его момент инерции увеличился в 4 раза.

4.3. Работа и кинетическая энергия вращающегося тела

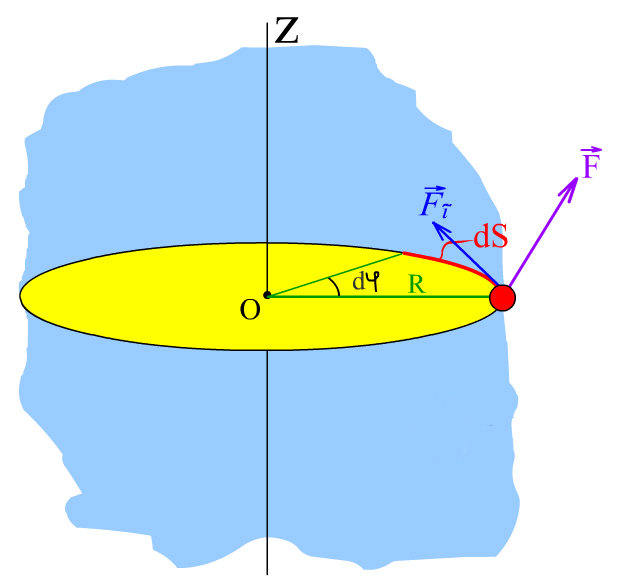
Рис.4.5

Пусть на твердое тело действует сила . Можно показать, что вращающий момент оси создает только составляющая силы , касательная к траектории точки ее приложения. За время тело поворачивается на бесконечно малый угол и точка приложения силы проходит путь Вектор направлен по касательной к дуге , поэтому работа силы определяется выражением: . (1.4.9)

Кинетическая энергия вращающегося тела определяется суммой кинетических энергий его элементарных объемов, которую с учетом выражения ( ), равна:

. (1.4.10)

В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия складывается из энергии поступательного движения и энергии вращения:

, (1.4.11)

где – масса скатывающегося тела; – скорость центра масс тела; – момент инерции тела относительно оси, проходящей через центр масс; – угловая скорость вращения.