2.2. Расчет передаточной функции второго звена электрического фильтра.
Принципиальная схема электрической цепи звена представлена на рис.2.3.
U’3(p)
U’4(p)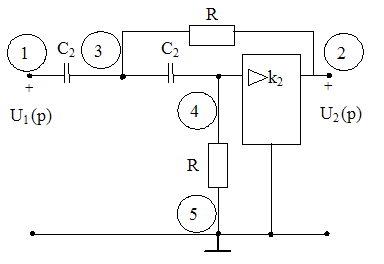
Рис.2.3
Представим схему замещения второго звена (рис. 2.4).
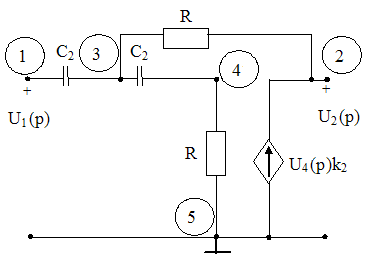
Рис.2.4
2.2.1.Узловые уравнения 2-го звена в общем виде.
Выберем узел 5 в качестве опорного узла . Тогда U’5(p) = U’0(p)=0.
Для расчета передаточной функции достаточно записать уравнения для узлов (3) и (4):
Узел №3:
(2.15)
Узел №4:
(2.16)
Уравнение
связи:
(2.17)
2.2.2.Расчёт коэффициентов левой части уравнений (2.15) и (2.16).
,
,
,
,
,
,
,
.
2.2.3.Расчёт правой части уравнений.
,
2.2.4.Уравнения (2.15) – (2.17) с учетом найденных коэффициентов.
(2.18)
(2.19)
(2.20)
2.2.5. Расчет передаточной функции второго звена.
Из
уравнения (2.20) выразим
:
,
(2.21)
Подставим
(2.21) в (2.19) и выразим
:
,
(2.22)
Уравнения
(2.21) и (2.22) подставим в (2.18) и выразим
через
:
(2.23)
В результате решения уравнений найдем передаточную функцию звена:
,
(2.24)
Преобразуем
выражение для передаточной функции. С
этой целью разделим числитель и
знаменатель на коэффициент
при
операторе
:
(2.25)
Добротность и частота полюса:
,
2.3. Расчет операторной передаточной функции электрического фильтра.
Передаточная функция фильтра при каскадном соединении звеньев:
(2.26)
3. Расчётеые выражения и графики ачх и фчх передаточнных функций фильтра.
Расчётные
выражения для частотных характеристик
АЧХ и ФЧХ фильтра получим путём подстановки
в выражение
(2.26). Обе зависимости, построенные в
широком диапазоне частот, определяют
характер преобразования сигнала и тип
фильтра.
3.1. Ачх и фчх передаточной функции первого звена фильтра.
Выражения для комплексной передаточной функции первого звена фильтра получим на основании (2.14), подставив в него :
(3.1)
Учитывая,
что
,
выражение (3.1) примет следующий вид:
,
Умножив числитель и знаменатель дроби на сопряженное знаменателю, получим:
Выражение для АЧХ примет вид:
Выражение для ФЧХ:
Построим графики АЧХ и ФЧХ с помощью графического редактора Mathcad. Для этого представим (3.1) функцией аргумента ω :
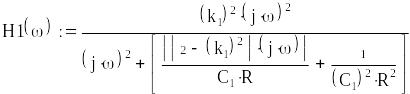
Графики АЧХ передаточной функции первого звена приведены на рис. 3.1 и на рис. 3.2 соответственно в линейном и логарифмическом масштабах.
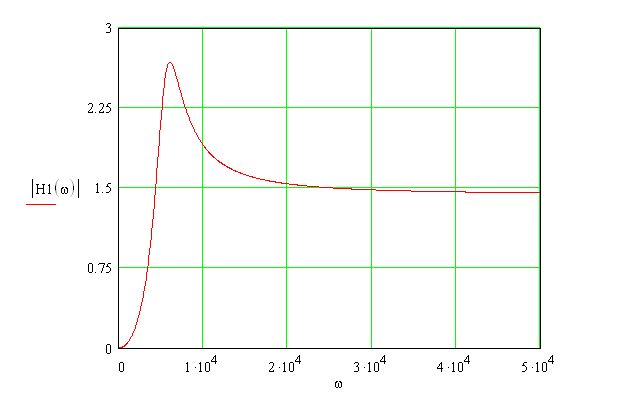
Рис.3.1
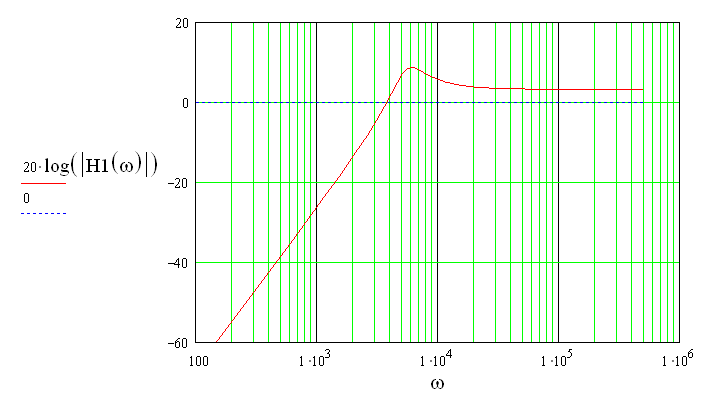
Рис.3.2
График ФЧХ передаточной функции первого звена:
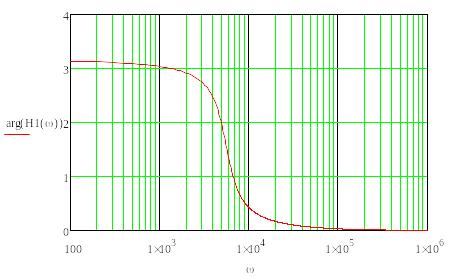
Рис.3.3