1.4. Спектральный анализ прохождения апериодического сигнала через активный фильтр

Задача выделения диапазона энергетически значимых частот из бесконечного множества гармонических составляющих апериодического сигнала решается в работе методом спектрального анализа. Определение этих частотных диапазонов необходимо при проектировании электронных преобразовательных и фильтрующих устройств.

Спектральный метод анализа процессов в электрических цепях состоит из трех частей: частотных характеристик передаточной функции электрической цепи, частотных спектров сигналов и собственно спектрального метода анализа – определение спектральной плотности выходного сигнала по спектральной плотности входного сигнала и частотным характеристикам передаточной функции.

Можно рекомендовать следующий алгоритм спектрального анализа [4]:

- апериодический входной сигнал, заданный в виде графика, представить функцией времени на интервале длительности импульса ;

- определить спектральную плотность входного сигнала на основании прямого интегрального преобразования Фурье:

- выполнить расчёт комплексной передаточной функции электрической цепи ;

- определить спектральная плотность выходного сигнала :

Так как в курсовой работе требуется именно частотное представление выходного сигнала, то обратный переход от к не представляет практического интереса и здесь не рассматривается. В свою очередь спектральная плотность может быть представлена в виде двух соотношений:

,

где - АЧХ передаточной функции электрического фильтра;

- амплитудный спектр входного сигнала =| | ;

- амплитудный спектр выходного сигнала =| |.

,

где - ФЧХ передаточной функции электрического фильтра;

- спектр фаз входного сигнала =arg ;

- спектр фаз выходного сигнала =arg .

Ширина спектра апериодического сигнала определяется, как часть спектра, в которой сосредоточена заданная доля (90 или 95%) энергии сигнала. Решение этой задачи основано на теореме Релея – равенстве Парсеваля для интеграла Фурье. В соответствии с этой теоремой распределение энергии апериодического сигнала по частоте можно определить из выражения [6]:

,

где - спектральная плотность энергии сигнала.

Энергию входного и выходного сигналов, которая переносится гармоническими составляющими, лежащими в диапазоне частот , можно найти, заменив в приведённом выражении пределы интегрирования на и на или на .

1.5. Устойчивость активных электрических цепей. Критерии устойчивости.

Введем понятия устойчивой и неустойчивой цепи. Цепь называется устойчивой, если свободные колебания с течением времени стремятся к нулю. В противном случае цепь называется неустойчивой. Из теории переходных процессов следует, что цепь является устойчивой, если корни характеристического уравнения лежат в левой полуплоскости комплексной переменной р. Если корни такого уравнения лежат в правой полуплоскости, то цепь является неустойчивой, т. е. она находится в режиме самовозбуждения [2].

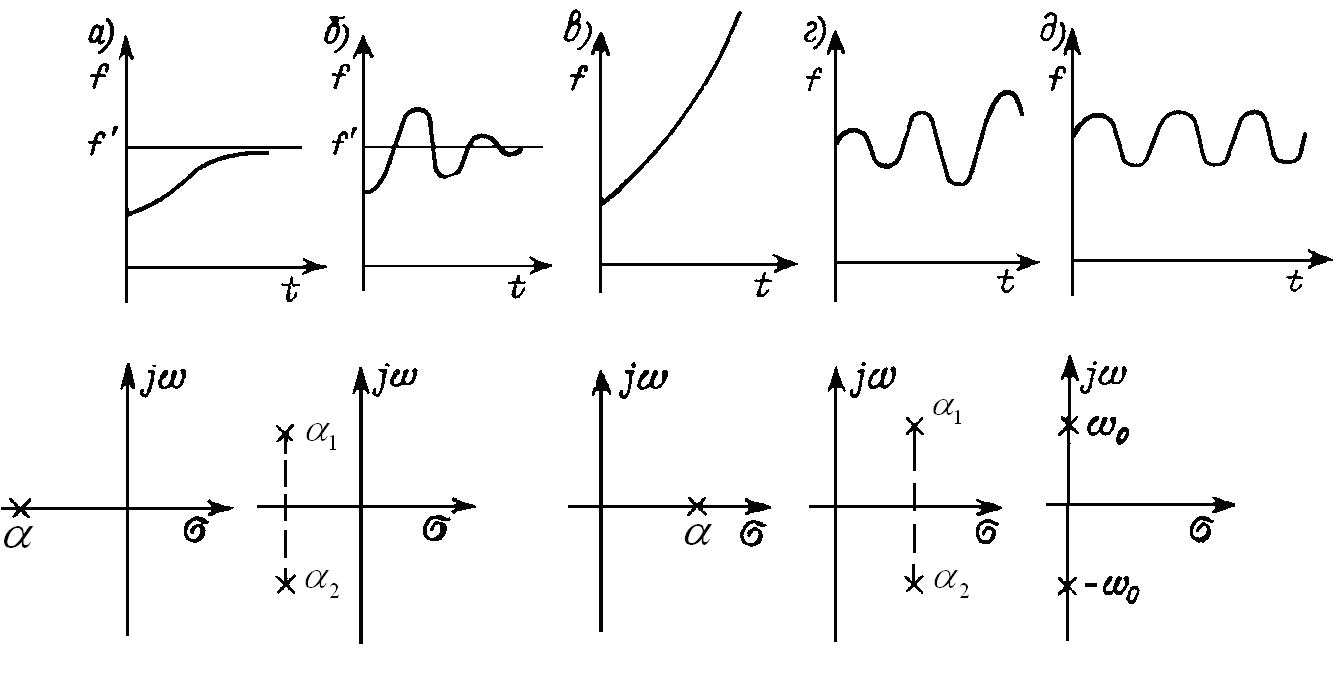
Рис. 1.7

Поэтому в устойчивой цепи, в которой свободная составляющая f" стремится с течением времени к нулю, все вещественные корни характеристического уравнения должны быть отрицательными (рис. 1.7, а), а комплексные — иметь отрицательную вещественную часть (рис. 1.7.1, б). Это же относится к кратным корням.

Если хотя бы один из корней располагается в правой полуплоскости (рис. 1.7, в, г), цепь является неустойчивой. Устойчивыми являются пассивные цепи, составленные из R-, L-, С-элементов. Цепи без потерь (включающие только L и С) находятся на границе устойчивости, поскольку их характеристические уравнения имеют чисто мнимые корни, отвечающие собственным частотам цепи . Такому положению корней соответствует незатухающий переходный процесс (рис. 1.7, д).

Неустойчивость может наблюдаться в активных электрических цепях с обратными связями. В этих цепях энергия, накапливаемая пассивными элементами при переходном процессе, восполняется управляемыми источниками, что может привести к неограниченному росту напряжений и токов при ограниченном внешнем воздействии [2].

Анализ устойчивости производится по расположению корней характеристического полинома передаточной функции исследуемой цепи на комплексной плоскости. При этом можно непосредственно находить значения корней (полюсов передаточной функции) или воспользоваться для этой цели критериями устойчивости.

Для определения полюсов передаточной функции характеристический полином каждого звена электрического фильтра следует приравнять к нулю и найти их корни. Такой подход рекомендуется применять для полиномов порядка не более третьего.

Оп­ределение корней для цепей высокого порядка является громоздкой процедурой. Поэтому в этом случае необходимо располагать критерием, который по виду характеристического полинома позволял бы судить об отсутствии корней ха­рактеристического уравнения в правой полуплоскости р.

Критерий устойчивости Рауса — Гурвица. Он относится к ал­гебраическим критериям устойчивости и позволяет по значениям коэффициентов b_т, b_т-₁, ..., b_o характеристического уравнения (14.23), без определения его корней, узнать является ли исследуе­мая цепь устойчивой.

Критерий формулируется следующим образом: цепь с об­ратной связью является устойчивой, если полином характе­ристического уравнения, является полиномом Гурвица. При этом используется основное свойство полинома Гурвица: все его корни находятся в левой полуплоскости комплексной перемен­ной р.

Для того, чтобы многочлен b_тр^т +b_m-1p^m-1 + ... + b₁p + b₀ яв­лялся полиномом Гурвица, необходимо и достаточно, чтобы были положительными определитель Рауса —Гурвица [1]:

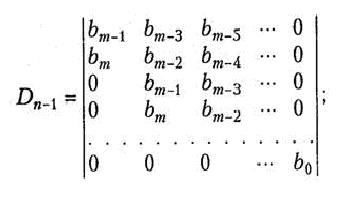
и все главные миноры этого определителя.

При составлении определителя Гурвица можно руководство­ваться следующим правилом. В первой строке записываются ко­эффициенты полинома Гурвица через один, начиная со второго. Во второй строке записываются коэффициенты полинома через один, начиная с первого. Вторая пара строк формируется путем смеще­ния первой пары строк на одну позицию. Третья пара — смещени­ем второй пары строк еще на одну вправо и т. д.

Примечание: для цепей первого и второго порядка необходимым и достаточным условием устойчивости является положительность значений всех коэффициентов характеристического полинома.

Критерий устойчивости Найквиста. Он относится к частотным критериям и основан на анализе частотных свойств цепи по петле обратной связи. Его можно сформулировать в геометрической трактовке так: система с обратной связью будет устойчивой, если годограф комплексной передаточной функции по петле обратной связи при изменении ω от 0 до ∞ не охватывает точку с координатами (+1;j0), где - передаточная функция усилителя; - передаточная функция цепи обратной связи [1].

Для расчёта передаточной функции электрическую цепь необходимо преобразовать: разорвать цепь обратной связи на входе усилителя и замкнуть входные полюса фильтра. В результате для звена фильтра (рис. 1.5) получим расчетную схему, приведенную на рис.1.8.

Рис. 1.8

Комплексная передаточная функция по петле обратной связи для нее равна:

Решив систему узловых уравнений, найдем выражение для передаточной функции в следующем виде:

Из полученного выражения видно, что для устойчивости цепи коэффициент усиления должен быть k<4. Если же k=4, то звено фильтра будет находиться строго на границе устойчивости ( ), при этом частота свободных колебаний будет .