21. Формулы для расчета оптимального заказа.

Для расчета наиболее экономичного размера заказа EOQ используется формула Уилсона:

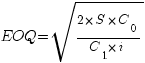
 — годовое потребление,

 - затраты на выполнение заказа,

 — цена единицы продукции,

 — затраты на содержание запасов (%).

C помощью формулы Уилсона можно рассчитать оптимальный размер заказа в соответствии с конкретными условиями деятельности предприятия. В случае если запасы пополняются не мгновенно, а в течение определенного периода времени (например при пополнении запасов за счет собственного производства), то используется следующая формула для расчета наиболее экономичного размера заказа EOQ:

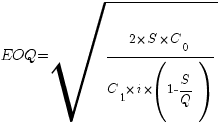
 — объем выпуска продукции, за счет которой пополняются запасы.

В условиях дефицита товаров, являющихся запасами, наиболее экономичный размер заказа EOQ определяется по формуле:

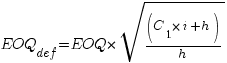
 — наиболее экономичный размер заказа без учета дефицита,

 — издержки, обусловленные дефицитом.

22. Формулы для расчета максимально возможной прибыли при управлении заказами.

Если Вы купили товар (валюту) по одной цене, затем продали его по другой, то прибыль или убыток составит разницу между ценой продажи и ценой покупки умноженной на сумму сделки.

Прибыль или убыток = Сумма сделки * (Цена продажи - Цена покупки)

В общем виде формула расчета прибыли  и убытков (по-английски profit and loss или просто  profit/loss) выглядит следующим образом:

Profit/Loss = N lots*100 000*(Sell – Buy) – N lots* Commission – N lots*100 000*Overnight*N days/365,

где N lots – количество лотов по 100 000, которое использовал трейдер,

       Sell – цена продажи базовой валюты

        Buy – цена покупки базовой валюты

        Commission – комиссионные, взимаемые диллинговой компанией

       Overnight – разница в ставках между базовой валютой и контрвалютой для операций Sell                            или Buy, в зависимости от совершенных трейдером операций. Взимается только в случае, если трейдер не успел закрыть позицию в тот же день. Она может быть как положительной (оплачивается за счет трейдера), так и отрицательной (доплачивается трейдеру)

        N days – количество дней, через которое трейдер закрыл позицию.                            

23. Стратегии уменьшения потерь при управлении запасами.

24. Риск дефицита и уровень обслуживания. (раздатка 5)

а — риск дефицита.


Psl — сервисный уровень, уровень обслуживания (service level)

При использовании MS Excel для расчетов, требующих вычисления интегралов от нормального распределения, можно использовать следующие функции:

Риск возникновения дефицита при запасе, отклоняющемся от среднего на z единиц:

α= 1-НОРМСТРАСП(z) или α =1-NORMSDIST(z).

Отклонение запаса от среднего, обеспечивающее заданный риск дефицита:

z =НОРМСТОБР(1-α) или z =NORMSINV(1-α)

Количество не обслуженных клиентов:

E(Psl)=(1-Psl)Q или E(z)=Sl*((1/корень(2п))*exp(-(z^2)/2)-za)

Риск возникновения дефицита и уровень обслуживания.

Вероятность (риск) возникновения дефицита определяет долю заказов, при ожидании которых был зафиксирован дефицит. Пусть, например, менеджер работал в течение 100 месяцев, делая в среднем 1 заказ в месяц на восполнение запаса некоторого товара. Если риск возникновения дефицита поддерживался науровне в 5%, это значит, что в 5 месяцах из 100 у него возникал дефицит, т.е. спрос превышал запас, оставленный на время ожидания поставки. Эта цифра не говорит, однако, ничего о том, как велик был дефицит в каждом из 5-ти месяцев, когда он был зафиксирован, и сколько клиентов за все время работы (или в среднем за каждый из этих 100 месяцев) остались не обслуженными. Вместе с тем, именно эта последняя величина наиболее наглядно характеризует уровень обслуживания клиентов с точки зрения менеджера.

Уровень обслуживания Psl (по-английски service level) – это средняя доля отказов продать 1 единицу данного товара в период между заказами. Например, если уровень обслуживания, который хотят поддерживать менеджеры фирмы, равен 99,9%, а количество единиц товара, продаваемых в период между последовательными поставками новых партий товара, равно Q =1000 шт., то это значит, что в среднем число отказов в продаже 1 единицы товара E =1. Вообще говоря,

E=Q*(1-Psl)

Между средней долей отказов E и риском возникновения дефицита существует непростая связь:

E(a)=sx*((1/корень(2п)*e^(-(z^2)/2)-z*a) (20)

где, в соответствие с (17) za=НОРМСТОБР(1-a).


Следует подчеркнуть, что часто воспринимаемая как «очевидная» связь

Psl=1-a
совершенно неверна (поэтому ее надо перечеркнуть).

Причина возникновения этого неверного представления – в непонимании смысла величины риска дефицита. Если, как в приведенном выше примере, риск возникновения дефицита равен 5%, т.е. случается в среднем 5 раз на 100 периодов между заказами, то понятно, что средняя на период доля отказов должна быть гораздо меньше. Ведь в 95-ти периодах дефицита не было и, следовательно, отказов не было вообще! В 5-ти периодах дефицит был, и трудно сразу сказать, какое количество отказов произошло в этих периодах. Однако, при взгляде на нормальное распределение видно, что вероятность большого числа отказов намного меньше, чем малого. Поскольку все произошедшие в 5 периодов отказы нужно «размазать» по 100 периодам, чтобы получить среднее число отказов за период, становится ясно, что отличие уровня обслуживания от 1

намного меньше, чем a. Используя формулу (20), можно получить, что при

Q=1000 и sx=50, при a=5%, среднее число отказов за период между заказами

E = 1,045, а P = 99,9% (примерно)