Нормальное распределение
Стандартное нормальное распределение
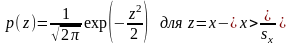
Соответствующие функции Excel для стандартного нормального распределения:
= Норм.Ст. Расп(z,интегральная) – стандартное нормальное интегральное распределение, где:
Z – значение, для которого строится распределение
Интегральная – логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМ.СТ.РАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается весовая функция распределения.
= Норм.Ст.Обр.(вероятность) – обратное значение стандартного нормального распределения, где:
Вероятность – вероятность, соответствующая нормальному распределению.
Эти распределения имеют среднее, равное нулю, и стандартное отклонение, равное единице.
Для заданного значения вероятности функция НОРМ.СТ.ОБР находит значение z, при котором НОРМ.СТ.РАСП(z) = вероятность. Таким образом, точность функции НОРМ.СТ.ОБР зависит от точности функции НОРМ.СТ.РАСП. В функции НОРМ.СТ.ОБР для поиска применяется метод итераций.
Zα = Норм.Ст.Обр.(1 – α), а (1 – α) = Норм.Ст.Расп.(Zα)
Пример: в MS Project «46-47 Снеси-Построй», в MS Word «46-47 Снеси-Построй (решение задачи)» и документ MS Excel «Снеси-Построй» вкладка «Снеси-Построй PERT»