44. Сетевые диаграммы при планировании проекта: вероятностное распределение времени выполнения отдельных этапов проекта. Pert: расчет среднего ожидаемого времени выполнения проекта и его дисперсии.

В настоящее время широко распространенны две взаимосвязанные методики количественного анализа проектов – CPM (Critical Path Method, т.е. метод критического пути) и PERT (Program Evaluation and Review Technique, метод анализа и обзора проекта), включающий в анализ вероятностные аспекты, связанные с неопределенностью в длительностях отдельных стадий проекта.

Метод CPM используется в условиях полной определенности при планировании и анализе проектов, данный метод основан на определении временных резервов всех стадий проекта. Успешное применение этой концепции обусловлено точным определением длительности каждой стадии проекта.

В случае, если время выполнения тех или иных стадий проекта подвержены случайным вариациям (что в реальности, конечно, так и есть), то понятия критических стадий и критического пути размываются. В этом случае, выводы об окончании проекта могут носить лишь вероятностный характер. Можно определить среднее время окончания «критического пути», средние длительности выполнения работ по путям, близким к «критическому», средние длительности всех путей, ведущих от начала проекта к его концу, однако это еще не даст ясного представления о сроках окончания проекта. Основной величиной, дающей такое представление, становится вероятность окончания проекта к заданному сроку (объявленному заказчику и согласованному с ним). Оценка этой вероятности (а также вероятности того, что финансовые затрату по проекту не превысят заданной величины) и посвящена методика PERT (program evaluation and review technique).

1. Распределение длительности отдельных стадий проекта

• Оптимистичная оценка t_opt

• Пессимистичная оценка t_pes

• Наивероятнейшая длительность t_m

Бета-функция:

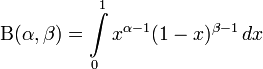
где α, β > 0 произвольные фиксированные параметры. При этом плотность распределения случайной величины X задаётся плотностью вероятности, имеющей вид:

2. Среднее значение и стандартное отклонение для длительности каждой стадии проекта

3. Оценка продолжительности проекта в целом и ее стандартное отклонение

Для каждого пути от старта к финишу

Для проекта в целом в качестве оценки длительности и стандартного отклонения выбирают T_path и σ²_path для критического пути. Для вычисления средней длительности пути достаточно сложить средние длительности этапов, из которых он состоит.

4. Вероятность выполнения проекта к определенному сроку

Время выполнения любого пути в проекте (в том числе и критического) можно считать распределенным нормально со средним значением T_path и дисперсией σ²_path.

Пример: в MS Project «46-47 Снеси-Построй», в MS Word «46-47 Снеси-Построй (решение задачи)» и документ MS Excel «Снеси-Построй» вкладка «Снеси-Построй PERT»

44. Вероятность выполнения проекта точно в срок. Пессимистическая и оптимистическая оценки длительности проекта. Назначение даты завершения проекта с учетом допустимых рисков.

Рассчитать вероятность выполнения проекта в целом к заданному сроку очень сложно, т. к. пути на сетевой диаграмме не являются независимыми и вероятности выполнения всех путей к заданному сроку нельзя перемножить, для оценки вероятности того, что каждый путь к заданному сроку будет завершен. Тем не менее, представление о вероятности окончания проекта в целом к заданному времени T_финиш можно получить, вычислив следующие два числа:

• вероятность окончания критического пути ко времени T_финиш можно рассматривать как завышенную оценку вероятности окончания всего проекта к этому времени («оптимистическая» оценка искомой вероятности – t_opt): нижняя граница для времени выполнения стадии – «раньше ни за что не успеть»

P_о-project = P_{критический путь}

• произведение вероятностей окончания всех путей, идущих от начала проекта к его концу, даст явно заниженную (грубую) оценку искомой вероятности («пессимистическая» оценка – t_pes): верхняя граница для времени выполнения стадии – «дольше уж вряд ли затянем»

P_p-project = P_path1 * P_path2 * P_path3 * … * P_pathN

В интервале между этими двумя оценками и лежит интересующая нас вероятность (t_mod). В рассматриваемом ниже примере анализа проекта по методу PERT мы увидим, что если задавать разумные значения T_финиш , отвечающие достаточно высоким значениям этих вероятностей (что только и представляет интерес с практической точки зрения), то упомянутый выше интервал сужается.

Для того чтобы вычислить вероятность завершения любого пути, идущего от начала к концу проекта, к заданному времени T_финиш, достаточно знать среднее (ожидаемое) время завершения этого пути <T_path> и стандартное отклонение этого времени s_path, которые вычисляются по формулам (1) и (4) соответственно. В таком случае, основной проблемой практического использования метода PERT становятся оценки среднего (ожидаемого) времени t_i и стандартного отклонения s_i для каждой стадии проекта.

Для нахождения вероятности P окончания пути к определенному заданному сроку T_finish c помощью MS Excel используем стандартная функция Excel = Норм.Расп ( z), где z: