МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный инженерно-экономический университет»

Филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Санкт-Петербургский государственный инженерно-экономический университет» в г. Твери

Кафедра гуманитарных, социально-экономических

и естественнонаучных дисциплин

НОВИК В.А.

ЛИНЕЙНАЯ АЛГЕБРА

Методические указания к выполнению контрольной работы

Направление подготовки 080100 «Экономика»

Профиль подготовки – Экономика предприятий и организаций

Отраслевая специализация –

Квалификация – бакалавр

Заочная форма обучения

Тверь 2012

Рекомендации по написанию контрольной работы

1. Общие положения.

Контрольная работа представляет собой самостоятельную письменную работу, целью которой является более глубокое усвоение учебного материала, предусмотренного программой учебной дисциплины «Линейная алгебра».

Выполнение контрольной работы прививает навыки самостоятельной исследовательской работы: целенаправленное изучение специальной литературы, оперирование основными понятиями науки. Написание контрольной работы на заочной форме обучения является обязательным при изучении дисциплины и предусмотрено учебным планом. Ее результат влияет на оценку знаний студента.

Выбор варианта контрольной работы.

Номер варианта выполняемой работы определяется путём деления шифра(номера зачётной книжки) на 20 и равен остатку, получающемуся при делении. Например, для зачётной книжки №1773 это вариант №13.

2. Порядок выполнения работы.

В целях успешного выполнения контрольной работы рекомендуется соблюдение следующего порядка ее выполнения.

Предъявление контрольной работы.

Работа должна быть представлена на проверку до начала экзаменационной сессии. После чего она сдаётся специалисту на кафедру с замечаниями преподавателя.

В случае отрицательной оценки контрольная работа должна быть переработана. Студент, не получивший положительной оценки за контрольную работу, к экзамену не допускается.

Учебно-методическое обеспечение

Основная и дополнительная литература

1. Рекомендуемая литература (основная)

1. Кремер Н.Ш. Высшая математика для экономистов. М., 2010

2. . Щипачев В.С. Задачник по высшей математике. М., Высшая школа 2003

2. Рекомендуемая литература (дополнительная)

3. .Красс М.С., Чупрынов Б.П. Основы математики и ее приложение в экономическом образовании. М., «Дело», 20008

Теоретические вопросы к экзамену

1. Вектора и действия над ними.

2. Действия над векторами заданными в базисе.

3. Уравнение прямой с угловым коэффициентом.

4. Уравнение прямой, проходящей через точку в данном направлении.

5. Уравнение прямой, проходящей через две точки.

6. Общее уравнение прямой и его исследование.

7. Угол между прямыми.

8. Общее уравнение плоскости.

9. Матрица. Действие над матрицами.

10. Минор, алгебраическое дополнение. Ранг матрицы.

11. Определитель. Свойства определителей.

12. Способы вычисление определителей.

13. Обратная матрица, нахождение обратной матрицы.

14. Теорема Крамера.

15. Метод Гаусса. Метод Жордано-Гаусса. Сходство и различие.

16. Матричный способ решения систем линейных уравнений.

17. В каком случае вектора называются линейно зависимыми и в каком – линейно -независимыми?

18. Что называется базисом на прямой, на плоскости и в пространстве ?

19. Формулы деления отрезка в данном отношении.

20. Что называется векторным произведением двух векторов?

21. Что называется смешанным произведением трех векторов?

22. Уравнение плоскости, проходящей через три точки?

23. Как вычисляются углы между двумя плоскостями и между прямой и плоскостью?

24. Каковы канонические уравнения эллипса, гиперболы и параболы?

25. Что называется комплексным числом? Как изображаются?

26. Какие действия производятся над комплексными числами?

27. Что называется алгебраической, тригонометрической и показательной формами записи комплексного числа?

28. Что называется модулем и аргументом комплексного числа?

29. Формула Муавра.

30. Собственные значения и собственные векторы линейных операторов.

Контрольная работа №1

Задача 1

1.1-1.20. Даны координаты точек А,В,С. Найти уравнения сторон треугольника АВС. Найти уравнение одной из медиан треугольника АВС. Найти уравнение одной из высот треугольника АВС. Найти уравнение одной из биссектрис треугольника АВС. Найти площадь треугольника АВС.

вариант	А	В	С	вариант	А	В	С
1.1	(1;2)	(2;0)	(-1;1)	1.11	(1;3)	(3;0)	(-1;1)
1.2	(2;1)	(1;0)	(-1;2)	1.12	(3;1)	(1;0)	(-1;3)
1.3	(2;1)	(1;1)	(-1;2)	1.13	(3;0)	(1;1)	(-1;3)
1.4	(2;1)	(1;0)	(1;-1)	1.14	(3;-1)	(1;0)	(1;1)
1.5	(-1;0)	(2;1)	(1;-1)	1.15	(-1;0)	(3;1)	(1;-1)
1.6	(1;-1)	(-1;0)	(2;1)	1.16	(1;-1)	(-1;0)	(3;1)
1.7	(1;-2)	(0;1)	(2;-1)	1.17	(1;-3)	(0;1)	(3;-1)
1.8	(2;-1)	(1;-2)	(0;1)	1.18	(3;-1)	(1;-3)	(0;1)
1.9	(-2;1)	(-1;-2)	(1;2)	1.19	(-3;1)	(-1;-3)	(1;3)
1.10	(2;2)	(-2;1)	(1;1)	1.20	(-3;3)	(3;1)	(1;1)

Указания к задаче.

Для решения задачи 1 (прямая линия на плоскости) следует использовать следующие сведения:

1). Угол наклона прямой к оси ОХ – это тот угол, на который нужно повернуть ось ОХ, чтобы она совпала с данной прямой (или оказалась параллельной ей). Как обычно, угол положителен, если по­ворачиваем против часовой стрелки, и отрицателен, если поворачи­ваем по часовой стрелке. Будем обозначать его буквой φ.

2). Угловой коэффициент прямой - это тангенс угла наклона пря­мой к оси ОХ. Будем обозначать его буквой k. Следовательно. k = tgφ (1)

3). Уравнение прямой с угловым коэффициентам

Если прямая не параллельна оси OY (рис. I), то ее уравнение y=kx+b, (2)

где b - координата точки пересечения прямой с осью OY, k - угловой коэффициент прямой, (x,у) - координаты любой точки на прямой.

Если прямая параллельна оси OY (рис. 2), то ее уравнение x = a, (3)

где a – абсцисса точки пересечения прямой с осью OX.

4). Уравнение прямой, проходящей через точку М₀(x₀,y₀) и имеющую угловой коэффициент k, y-y₀₌k(x-x₀), (4)

где (x₀,y₀) - координаты заданной точки на прямой, k - угловой коэффициент прямой, (x,y) - координаты любой точки на прямой.

5 ). Уравнение прямой, проходящей через две заданные, точки М₁(x₁,y₁) и М₂(x₂,y₂):

(5)

где ; (x₁,y₁) - координаты одной точки на прямой, (x₂,y₂) - координаты другой точки на прямой, (x,y) - координаты любой точки на прямой.

6). Общее уравнение прямой: Ax + By +C=0, (6)

где A, B, С - заданные числа, причем А и В одновременно в нуль не обращаются. (x,y) - координаты любой точки на прямой.

Е сли В не обращается в нуль, то уравнение (6) можно преобра­зовать следующим образом: (6')

Тогда, сопоставив формулы (6') и (2), имеем:

7). Условие параллельности двух прямых k₁=k₂; (7)

где k1 и k2 - угловые коэффициенты прямых.

8). Условие перпендикулярности двух прямых k₁·k₂=-1, (8)

где k₁ и k₂ - угловые коэффициенты прямых.

9). Нахождение координат точки пересечения двух прямых.

Е сли две непараллельные прямые заданы своим уравнениями: A₁X+B₁Y+C₁=0 и A₂X+B₂Y+C₂=0, то координаты точки пересечения этих прямых - есть решение системы уравнений: (9)

10). Нахождение координат середины отрезка

Е сли точка А имеет координаты (x_а,y_а), а точка В - (x_ь,y_ь), то координаты середины отрезка АВ точки О можно найти по формулам:

(10)

11. Деление отрезка в данном отношении

Е сли точка А имеет координаты (x_а,y_а), а точка В - (x_ь,y_ь), то координаты точки С делящей отрезок АВ в отношении 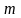:n можно найти по формулам:

(11)

12). Нахождение длины отрезка

Е сли точка А имеет координаты (x_а,y_а), а точка В - (x_ь,y_ь), то длину отрезка АВ можно найти по формуле:

(11)

13). Нахождение угла между прямыми:

, ,

13). Площадь треугольника. Пусть А₁(x₁,y₁), А₂(x₂,y₂), А₁(x₃,y₃)- вершины треугольника, тогда его площадь выражается формулой:

Рассмотрим несколько примеров применения приведенных формул.

Задача. Точки A(-2,1), В(5,-2) и С(0,4) являются вершинами треугольника ABC:

а) Найти уравнение медианы треугольника.

Р ешение. Обозначим середину стороны ВС буквой M, тогда координаты точки M найдем по формулам деления отрезка пополам.

Уравнения медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AM проходит через точки

А(-2;1) и М(2,5;1), поэтому:

б) Найти уравнение одной из сторон треугольника.

Р ешение. Сторона АВ проходит через точки A(-2,1) и В(5,-2), поэтому её

у равнение будем искать в виде . Подставляя координаты точек

получим

в) Найти уравнение одной из высот треугольника.

Р ешение. Найдём уравнение высоты СК, проходящей через С(0,4) перпендикулярно АВ: . Определим угловой коэффициент прямой АВ: 7у=-3х+1, k_АВ=-3/7. Угловой коэффициент СК найдём из условия перпендикулярности прямых k₁·k₂=-1, k_АВ·k_СК=-1, k_СК=7/3. Подставляя в уравнение y-y₀₌k(x-x₀), получим у-4 = 7/3( х – 0), у-4 = 7/3х, 7/3х-у+4 = 0

г) Найти площадь треугольника АВС .

Решение. Воспользуемся формулой