Метод стандартизации

В ряде случаев при плохой обусловленности матрицы улучшить ситуацию можно, используя операцию стандартизации матрицы. Суть стандартизации заключается в том, что матрицазаменяется матрицей, а векторзаменяется вектором, элементы которых связаны с элементами матрицыи векторасоотношениями

,

где

В результате такой замены исходная система уравнений приводится к виду

.

Решение этой системы может оказаться более точным, чем решение исходной системы, так как коэффициент обусловленности матрицы может быть меньше, чем коэффициент обусловленности матрицы.

Вектор связан с векторомсоотношениями

К сожалению, метод стандартизации не всегда приводит к положительному результату. Действительно, прежде всего следует отметить, что коэффициент обусловленности уравнения (2), используемого для определения вектора , Cond(F^TF) больше коэффициента обусловленности исходного уравнения CondF, т.к. Cond(F^TF)=(CondF)² и CondF>1. Следовательно, применение данной схемы увеличивает погрешность определения вектора . С другой стороны для определения вектора  необходимо обратить матрицу (F^TF)^-1, как известно операция обращения матрицы является наименее точной, что также увеличивает погрешность определения вектора .

С учетом сказанного метод наименьших квадратов целесообразно модифицировать таким образом, чтобы исключить указанные недостатки.

Метод Наименьших квадратов на основе матриц с ортоНормированнЫми столбцами

Рассмотрим систему уравнений с матрицей, состоящей из ортонормированных столбцов

(6)

Поскольку E^TE=I, то решение этого уравнения имеет вид

. (7)

Поскольку CondE^T=CondE=1, то в данном случае коэффициент обусловленности системы уравнений не изменяется и, кроме того, является минимально возможным (CondE1).

Найдем теперь выражение для оценки дисперсии i-той координаты вектора . Прежде всего отметим, что значение d_ii, входящее в выражение (3) равно 1. Действительно, поскольку в данном случае F=E и F^TF=E^TE=I и I^-1=I, то d_ii=1. Далее учитывая, что

для получим следующее выражение

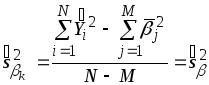, (8)

т.е. дисперсия одна и та же для всех координат вектора .

Если матрица ортогональна, но не нормирована, то приведенные выше формулы усложняются. Однако, если норма всех вектор столбцов матрицы E одинакова ( в случае матрицы Уолша норма вектор столбца равна N - размерности вектора), то формулы усложняются незначительно и принимают вид

Рассмотрим исходное уравнение

.

Разложим матрицу F в произведение двух матриц F=ET, где E - ортонормированная матрица размера N x M, T- верхнетреугольная матрица размера M x M. Поскольку ортонормированная матрица удовлетворяет следующим свойствам E^T=E^-1 , CondE=1, то для определения вектора  получим уравнение

.

Коэффициент обусловленности данного уравнения совпадает с коэффициентом обусловленности исходного уравнения и для решения данного уравнения не нужно обращать матрицу (поскольку система уравнений с треугольной матрицей может быть решена без обращения матрицы), следовательно, данная схема обладает более высокой точностью при определении вектора .