4.4. Сітьове планування з урахуванням вартості виконання робіт

Тривалість виконання окремих робіт може бути скорочена за рахунок залучення додаткових фінансових ресурсів. У таких випадках залежність вартості виконання проекту від терміну його виконання є спадною: більшій тривалості виконання проекту відповідають менші витрати, і навпаки – меншій тривалості виконання проекту відповідають більші витрати.

Але при затримці із закінченням проекту можуть мати місце додаткові збитки, пов’язані із штрафами за порушення умов контракту на виконання проекту. Тобто залежність втрат, пов’язаних із запізненням завершення проекту, є зростаючою від тривалості строку виконання проекту.

Постає проблема визначення такої стратегії виконання проекту, при якій загальні витрати, що пов’язані із виконанням проекту і з втратами внаслідок затримки із його завершенням, будуть мінімальними (рис.4.14)

Витрати (1)

Оптимум

Р івень

м інімальних загальних

витрат (2) (3)

t

Оптимальний

термін виконання

Рис.4.14.

Опрацюємо спочатку питання про оптимізацію сітьового графіка за показником вартості виконання проекту для випадку, коли задано директивний термін завершення всього комплексу робіт .

Нехай - множина вершин сітьового графіка, - множина його дуг. Припустимо, що тривалість роботи може змінюватись у певних межах від до одиниць часу, де - тривалість виконання цієї роботи, скажімо, у нормативному режимі, а - тривалість її виконання у максимально прискореному режимі.

Нехай - вартість виконання роботи у нормальному режимі, а - витрати на її виконання у максимально прискореному режимі. Припустимо, що залежність вартості від тривалості виконання є лінійною:

, (4.11)

що ілюструє рисунок 4.15.

В артість

Тривалість виконання

Рис. 4.15.

Тоді задача оптимізації сітьового графіка за показником мінімізації загальної вартості z виконання проекту, з урахуванням вимоги завершення проекту у заданий директивний термін , набирає вигляду:

Знайти ,

що належать області , визначеної умовами:

; (4.12)

(4.13)

(4.14)

і мінімізують функцію цілі:

(4.15)

Задача (4.12) – (4.15) є задачею лінійного програмування з двосторонніми обмеженнями на . Якщо її розв’язок існує, тобто коли є можливість виконати проект за директивний термін , результатом розв’язування задачі будуть такі тривалості виконання кожної з робіт , за яких вартість виконання всього проекту буде найменшою.

У загальному випадку задачу оптимізації сітьового графіка з урахуванням часу та вартості можна розглядати як двоцільову проблему:

(4.16)

в якій перша цільова функція орієнтує на найскоріше виконання проекту (терміну настання кінцевої події), а друга – на мінімізацію витрат, пов’язаних із виконанням проекту. Обмеження (4.12) – (4.14) визначають множину допустимих планів.

Таким чином, задачу (4.12) – (4.15) слід розглядати лише як спрощений підхід до розв’язання цільової проблеми оптимізації сітьового графіка. Наступним кроком здійснення цільової оптимізації буде дослідження задачі (4.12) – (4.15) як параметричної відносно директивного терміну виконання проекту . Це дозволить визначити залежність оптимальної вартості від (рис. 4.16), що є корисним для узгодження термінів виконання проекту та необхідних для цього витрат.

0

Рис. 4.16

Приклад 4.4. Розглянемо проект, сітьова модель якого наведена на рис. 4.17, а показники тривалості та вартості кожної із робіт надані у таблиці 4.5

2

Р-1 Р-3

3

1

Р-2

Рис.4.17

Таблиця 4.5

Робота, дуга	Тривалість, місяців		Вартість, тис. грн..
	мінімальна	максимальна	максимальна	мінімальна
Р-1 (1, 2)	3	5	10	6
Р-2 (1, 3)	5	8	15	12
Р-3 (2, 3)	3	4	8	5

Необхідно визначити тривалість та вартість виконання проекту за умов:

• тривалість кожної із робіт буде максимальною;

• тривалість кожної роботи буде мінімальною.

Побудувати графік залежності оптимальної вартості виконання проекту від директивної тривалості його виконання .

Розв’язування. 1. Побудуємо сітьовий графік проекту, обравши за тривалості робіт максимально можливі терміни їх виконання. Обчислимо також часові характеристики L, E усіх подій та повні резерви часу M усіх робіт подій проекту (рис. 4.18).

5

5

2

5 4

0

0

9

9

0

0

1 8 3

1

Рис. 4.18

Таким чином, максимальна тривалість виконання проекту (місяців). Оскільки кожна з робіт виконуватиметься з мінімальною вартістю, робимо висновок, що оптимальна вартість проекту при дорівнюватиме 6 + 12 + 5 = 23 (тис. грн.).

2. Проаналізуємо тепер проект за умов, коли тривалість виконання кожної з робіт буде мінімальною (рис. 4.19).

3

3

2

3 3

0

0

6

6

0

0

1 5 3

1

Рис.4.19.

Мінімальна тривалість виконання проекту місяців. Проте оптимальна вартість виконання проекту за 6 місяців не дорівнюватиме сумі максимальних вартостей виконання кожної із робіт 10 + 15 + 8 = 33 (тис. грн.). Це пояснюється тим, що робота (1, 3) не є критичною та має резерв часу М (1, 3) = 1 місяць. Отже, якщо цю роботу виконати не за 5, а за 6 місяців, тривалість виконання проекту не збільшиться. Але зменшиться вартість виконання роботи (1, 3) оскільки (5 місяців) = 15 тис. грн. /табл..6.7/, а (6 місяців) = (тис. грн.) /формула (4.11) та вихідні дані з табл. 6.7./, тобто оптимальна вартість виконання проекту за 6 місяців дорівнюватиме 10 + 14 + 8 = 32 (тис. грн.).

3. Щоб побудувати графік залежності оптимальної вартості виконання проекту від директивної тривалості його виконання , складемо задачу параметричного лінійного програмування, обравши за параметр :

Знайти ,

що належать області , визначеної умовами:

,

,

і мінімізують функцію цілі:

,

де

Розв’язок задачі параметричного програмування наведено на рис. 4.20. Бачимо, зокрема, що коли директивну тривалість проекту обрати такою, що дорівнює 8 місяців ( ), оптимальна вартість виконання проекту дорівнюватиме 25 тис. грн. ( ).

Рис. 4.20.

Досі при плануванні проекту враховувалися лише витрати, що пов’язані із скороченням термінів виконання окремих робіт. Далі опрацюємо питання про те, як додатково врахувати втрати, пов’язані із затримкою з виконанням проекту.

Отже, нехай - нормативний термін завершення проекту, - втрати, що пов’язані із затримкою закінчення проекту на одиницю часу понад нормативний термін його виконання.

Час затримки із виконанням проекту обчислюється за формулою:

де - термін настання кінцевої п-ої події сітьового графіка.

Тому додаткові витрати через затримку завершення проекту складуть величину st грошових одиниць. Щоб врахувати ці витрати при оптимізації сітьового графіка за показником мінімізації загальної вартості, до економіко-математичної моделі (4.12) – (4.16) слід ввести такі корекції:

1. замінити цільову функцію (4.16) на функцію:

, (4.17)

яка враховує як витрати, що пов’язані із виконанням проекту (перший доданок), так і втрати внаслідок закінчення проекту із запізненням понад нормативний термін (другий доданок);

2. обмеження (4.14) 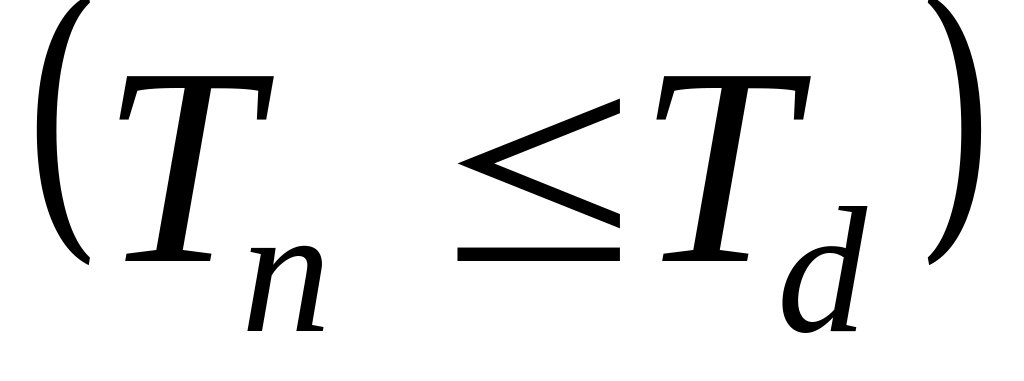замінити умовами, які відбивають можливість запізнення із закінченням проекту на термін t:

( 4.18)

В оптимальному плані скоригованої задачі значення t^* змінної t задовольнятиме умову:

(4.19)

тобто являтиме собою оптимальний термін можливої затримки із завершенням проекту понад нормативний термін , якщо це технологічно необхідно та економічно виправдано.