Порядок выполнения работы

1. В каталоге PHYS\ИмитЛаб\... найти файл ЛабФото.exe и за­пустить его.

2. Ознакомиться с краткой информацией, предоставляемой интерфей­сом программы и позволяющей продолжать работу дальше.

3. В режиме "Ввод данных" выбрать заданные для эксперимента световые волны.

4. В режиме "Демонстрация", нажимая любую клавишу, наблюдать из­менение силы фототока в зависимости от напряжения между электрода­ми для каждой длины волны, одновременно отслеживая ход эксперимента по информации в левом верхнем углу дисплея.

5. По окончании эксперимента в режиме "График" наблюдать се­мейство вольт-амперных характеристик I = f(U) для выбранных частот све­та и распечатать их

( или срисовать с экрана).

Обработка результатов измерений

1. Аппроксимировать экспериментальные точки графика непрерывны­ми кривыми (провести кривые по экспериментальным точкам).

2. По полученным графикам определить U_з для выбранных частот.

3. Построить график U_з = f(ν).

4. Методом наименьших квадратов рассчитать угловой коэффициент ̣̣tgα и

коэффициент корреляции.

5. По формуле (8) вычислить постоянную Планка.

Заключение

В произвольной форме сделать выводы о проделанной работе. Срав­нить полученное значение h с табличным.

Лабораторная работа № 3.23

Эффект комптона

Цель работы:

изучение дискретности электромагнитного излучения, определение численного значения комптоновской длины волны

Введение

Согласно выдвинутой Планком квантовой гипотезе электромагнитные волны излучаются не непрерывно, а отдельными порциями - квантами, энергия которых пропорциональна частоте колебаний

ε = hν,

где h – постоянная Планка, ν - частота колебаний электромагнитные волны.

Корпускулярная природа излучения предполагает наличие у кванта излучения импульса, равного

р = hν/с = h/λ,

где с – скорость распространения волны(скорость света), λ - длина волны.

Особенно отчетливо корпускулярные свойства электромагнитного излучения проявляются в явлении, которое получило название эффекта Комптона.

В 1923 г. А.Комптон, исследуя рассеяние рентгеновских лучей различными веществами, обнаружил, что в рассеянных лучах наряду с излучением падающей волны длиной λ, содержится также излучение большей длины волны λ’. При этом разность длин волн Δ λ = λ’ - λ зависит только от угла рассеяния θ, образуемого направлением рассеянного излучения с направлением падающей волны. От длины волны λ и от природы рассеивающего вещества Δ λ не зависит.

Этот эффект не может быть объяснен в рамках волновой теории, согласно которой длина волны при рассеянии изменяться не должна.

Теория эффекта была создана самим Комптоном на основе использования квантовых представлений о природе рентгеновского излучения при упругом рассеянии рентгеновских лучей на свободных (или слабосвязанных) электронах рассеивающего вещества. Если излучение представляет собой поток квантов, то эффект Комптона есть результат упругого столкновения этих кантов с электронами. В процессе этого столкновения квант излучения передает электрону энергию и импульс с соблюдением законов их сохранения. Так как энергия кванта рентгеновского излучения много больше кинетической энергии электрона, то последней можно пренебречь и импульс электрона до столкновения считать равным нулю.

Согласно релятивистскому закону сохранения энергии

Е_о + ε_γ = Е + ε_γ’, ( 1 )

где Е_о = m_oc² - энергия покоя электрона, ε_γ = hν - энергия квантов падающего излучения, Е = mc² - энергия электрона после столкновения, ε_γ’ = hν’ – энергия квантов рассеянного излучения.

Подставив в (1) приведенные выше значения слагаемых, получим закон сохранения энергии в следующей форме

m_oc² + hν = mc² + hν’. ( 2 )

Закон сохранения импульса при столкновении кванта излучения с электроном в соответствии с векторной диаграммой (рис. 1) выглядит следующим образом:

р_γ = р_е + р_γ’, ( 3 )

где р_γ - вектор импульса кванта излучения до столкновения, р_е - вектор импульса электрона после столкновения, р_γ’ - вектор импульса кванта излучения после столкновения.

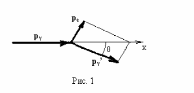Спроектировав вектора импульсов на ось х и подставив значения импульсов электрона (в релятивистской форме) падающего и рассеянного квантов, после возведения в квадрат, получим следующее уравнение:

(mv)² = (h/λ)² + (h/λ’)² - , ( 4 )

где m - релятивистская масса электрона, θ - угол рассеяния.

Совместное решение уравнений (2) и (4) приводит к формуле описывающей увеличение длины волны рассеянного излучения:

λ’ - λ = Δλ = 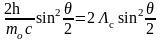. ( 5 )

Множитель Λ_с , выраженный через универсальные постоянные, называется комптоновской длиной волны электрона

Λ_с = 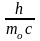. ( 6 )

Описание установки(программы)

Установка для реализации опыта Комптона, схема которой приведена на рисунке 2, состоит из источника рентгеновского излучения (рентгеновская трубка) 1, диафрагм 2, рассеивающего вещества 3, рентгеновского спектрографа 4, который может передвигаться по направляющим 5, регистрируя спектр под различным углам рассеяния.

Характеристическое излучение рентгеновской трубки 1, каллимированное диафрагмами 2, направляется на рассеивающее вещество 3. Рентгеновский спектрограф 4 регистрирует в отраженном луче два компонента излучения - отраженный без изменения длины волны (рассеяние на атомах) и с изменением длины волны (рассеяние на электронах) - и позволяет измерить длины волн рассеянного излучения при разных углах рассеяния.

Компьютерная программа имитирует рассеяние рентгеновских лучей при разных углах, которые выбираются в режиме «Ввод данных». В режиме «Демонстрация» демонстрируется работа установки при выбранных углах рассеяния. В режиме «Расчет» имитируется работа спектрографа - запись на фотопленку полос почернения от рассеянных рентгеновских лучей. Шкала спектрографа градуирована в ангстремах ( 1А = 10^-10 м).