Порядок выполнения работы

1. В каталоге Phys\ИмитЛаб\... найти файл ЛабБроун.exe и запустить его.

2. Ознакомиться с краткой информацией, предоставляемой интерфей­сом программы и позволяющей продолжать работу дальше.

3. В режиме "Ввод данных" выбрать заданные для исследования условия эксперимента (среду, размер броуновской частицы, температуру, промежуток времени наблюдения)

4. В режиме "Демонстрация" наблюдать движение броуновской час­тицы и ее траекторию.

5. В режиме "Расчет" запустить программу на расчет < x²> и теоретической скорости теплового движения <v_т>.

6. Для получения необходимой выборки при одной температуре операцию расчета повторить заданное число раз.

7. Результаты эксперимента перенести в рабочий журнал(или сохранить и распечатать).

8. Пункты 3 ÷ 7 повторить для других заданных температур.

Обработка результатов измерений

1. По формуле ( 6 ) рассчитать среднюю скорость теплового движения молекул.

2. Провести статистическую обработку результатов измерения средней скорости теплового движения молекул газа по сделанной выборке измерений, определив доверительный интервал и его надежность.

3. По формуле ( 5 ) рассчитать теоретическое значение <v_т> и построить график зависимости её от Т. Для расчета <v_т> рекомендуется использовать эту же программу.

4. Температурную зависимость средней скорости теплового движения моле­кул азота представить графически, нанеся экспериментальные точки с доверительным интервалом на те­оретическую кривую.

Заключение

В произвольной форме сделать выводы о проделанной работе.

Лабораторная работа N 1.23

Опыт перрена

Цель работы: Изучение распределения Больцмана, определение

числа Авогадро.

Введение

Законы аэростатики приводят к формуле, связывающей давление p на высоте Н в изотермической атмосфере c давлением на поверхности p_o и называемой барометрической формулой:

p = p_oexp (1)

где μ - молярная масса воздуха, g - ускорение свободного падения, R - универсальная газовая постоянная, T - температура воздуха.

Из молекулярно-кинетической теории известна формула, связывающая давление с концентрацией молекул n:

p = nkT .

Подставив последнее соотношение в (1) после несложных преобразо­ваний получим:

n = n_oexp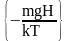 , (2)

где n – концентрация молекул на высоте Н , n_o - концентрация молекул у поверхности, m - масса отдельной молекулы, k - постоянная Больцмана.

Соотношение (2) описывает распределение молекул газа по значениям их потенциальной энергии Е_р = mgh и называется распределением Больцмана.

Распределение броуновских частиц в газе в силу малости их массы также должно подчиняться распределению Больцмана. Тогда для двух значений вы­соты можно записать:

N₁ = N_oexp ,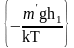

N₂ = N_oexp ,

где N₁ и N₂ – концентрация броуновских частиц на высотах h₁ и h₂ соответственно, m′ - масса броуновской частицы.

Логарифмируя отношение N₁/N₂ приходим к следующему выражению:

ln(N₁/N₂) = 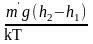= 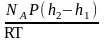(3)

где N_A = R/k - число Авогадро, m′g = Р - вес броуновской частицы(должен быть взят с учетом поп­равки на силу Архимеда, действующую в среде, где взвешена частица).

Соотношение (3) было использовано Перреном (1909 г.) для опреде­ления числа Авогадро:

N_A = (4)