
- •Розділ і. Предмет соціально-педагогічної діагностики та її історичний розвиток
- •1.1. Історіографія соціально-педагогічної діагностики
- •1.2. Предмет, сутність та функції соціально-педагогічної діагностики
- •Діагностичне дослідження соціального педагога
- •2.1. Структура й рівні соціально-педагогічної діагностики
- •Рівні соціально-педагогічної діагностики
- •2.2. Діагностичні процедури та критерії соціально-педагогічної діяльності
- •Діагностична професіограма соціального педагога
- •Діагностична програма вивчення рівнів вихованості учнів іv – іх класів
- •Діагностична програма вивчення рівнів вихованості учнів х – хі класів
- •Критерії вихованості особистості школяра
- •Критерії оцінки вихованості учнів
- •2.3. Якісні та кількісні методи соціально-педагогічної діагностики
- •Якісні діагностичні методи
- •Кількісні діагностичні методи
- •Вимір у педагогіці й психології
- •Табулювання даних і обчислення частот
- •Міри центральної тенденції
- •Результати тестування респондента а
- •Міри варіації (мінливості)
- •Кореляційна залежність
- •Оцінка сили кореляції
- •Оцінка сили кореляції
- •Розділ ііі. Діагностичні технології у соціумі
- •3.1. Методика діагностики сім’ї
- •3.2. Діагностика дитячих та молодіжних об’єднань
- •1.2. Методика „Bіяло” [2].
- •1.3. Методика „Розклади картинки” [2].
- •1.4. Методика „Справедливість” [2].
- •1.5. Методика „Математика та ввічливість” [3].
- •1.6. Методика „Що таке щастя?” [2]
- •1.7. Методика „Що ми цінуємо в людях?” [2].
- •1.8. Методика „Закінчи речення” [2].
- •1.9. Методика „Давайте обговоримо” [2].
- •1.10. Методика „Робота на конвеєрі” [2].
- •1.11. Методика „Спрямованість особистості” [2].
- •1.12. Методика „Емоційна спрямованість” [2].
- •1.13. Методика „Музичний образ” [2].
- •Іі. Кількісні методики індивідуальної роботи з учнем
- •2.3. Методика „Самооцінка скромності” [2].
- •2.4. Методика „Самооцінка колективізму” [2].
- •2.5. Методика „Ти громадянином бути зобов’язаний”.
- •19. А зараз, якщо знаєш, назви прізвище будь-якого театрального режисера та назву якої-небудь вистави, яку він поставив.
- •22. Які передачі по телебаченню ти любиш більш за все?
- •23. Які передачі по радіо (з перерахованих вище) ти любиш найбільше?
- •2.6. Методика „Відмітка за працьовитість” [2].
- •2.7. Методика „Трудовий досвід” [2].
- •Ііі. Якісні методики роботи з колективом
- •3.1. Методика колективістського самовизначення та його вивчення „у кожного Павла своя правда” [2].
- •3.2. Визначення ступеня емоційної єдності в класі. Методика „Естафета” [2].
- •3.3. Методика „Коло” [2].
- •3.4. Методика „Який у нас колектив?” [2]
- •3.5. Методика „Референтометрія” [2].
- •Іv. Кількісні методики роботи з колективом
- •4.1. Методика вивчення згуртованості групи „Що важливіше?” [2].
- •4.2. Методика „Скільки голів, стільки розумів?” [2].
- •4.3. Методика вивчення еталонності класного колективу „Ідеальний клас” [2].
- •4.4. Методика „Наші стосунки” [2].
- •4.5. Методика вивчення структури міжособистісних стосунків в учнівському колективі „Соціометрія” [2].
- •Матриця вибору
- •4.6. Методика „Вибір у дії” [2].
- •4.7. Методика „Відмітка другу” [2].
- •Матриця оцінок стосунків учнів
- •4.8. Методика вивчення положення школяра в системі міжособистісних стосунків „До кого ти звернешся?” [2].
- •4.9. Методика „Вибір однокласників” [2].
- •4.10. Методика „Референтометрія” (1 варіант) [2].
- •Додаток б діагностика сім’ї і. Якісні методики діагностики батьків [1]:
- •1.1. Психодіагностика мотиваційних і особистісних особливостей дорослої людини. Методика „Підставної самооцінки” е. Уваріної [1].
- •1.2. Анкета для батьків багатодітних сімей
- •Дякуємо за участь у дослідженні та щирі відповіді! іі. Кількісні методики діагностики батьків
- •2.1. Тест-опитувальник батьківського ставлення [7].
- •III шкала. „Симбіоз”
- •2.2. Методика „Вимірювання надії” [1].
- •2.3. Тест для визначення трьох станів особистості батьків [9].
- •2.4. Методика виявлення агресії [1].
- •Особистісні рейтинги агресії
- •Оцінка агресії за визначенням
- •2.5. Визначення спрямованості особистості (орієнтаційна анкета б. Басса) [1].
- •Бланк для підрахунку балів
- •2.6. Методика діагностики міжособистісних відносин. Тест Томаса [1].
- •2.7. Методика „Наша дитина” [2].
- •Ііі. Якісні методики
- •3.1. Методика „Вивчення мотивів взаємодії з дорослими”
- •3.2. Методика „Малюнок сім'ї” [11]. Опис тесту
- •1. Оцінка загальної структури
- •2. Визначення найпривабливішого персонажу
- •3. Дитина про себе
- •4. Додаткові персонажі
- •5. Батьківська пара
- •6. Ідентифікація
- •7. Відмова від зображення того або іншого члена сім’ї.
- •Іv. Кількісні методики
- •4.1. Методика вивчення потреби спілкування (пс) та потреби досягнення (пд).
- •V. Якісні методики
- •5.1. Анкета сімейних стосунків [7].
- •5.2. Методика ретроспективного аналізу біографій (раб) [9].
- •5.3. Анкета для виявлення ґендерної рівності в сім’ї та типу сім’ї.
- •5.4. Анкета дослідження проблем студентської сім’ї.
- •5.5. Алгоритм вивчення сім’ї [7].
- •5.6. Соціальний паспорт сім’ї [7].
- •5.7. Карта обстеження сімей, які мають неповнолітніх дітей [7].
- •Vі. Кількісні методики
- •6.1. Метод комплексної експрес-діагностики особливостей сімейної атмосфери, сімейного виховання і ставлення батьків до дітей [6].
- •6.2. Методика вивчення психологічної атмосфери сім’ї та сімейних відносин „Типовий сімейний стан” [7].
- •6.3. Тест „Кінетичний малюнок сім’ї” [7].
- •6.4. Анкета для подружжя „Який Ваш шлюб?” [10].
- •Додаток в Діагностика обдарованих дітей і. Якісні методики діагностики обдарованості дітей.
- •1.1. Анкета для батьків (а. Сизанов). Визначення рівня прояву здібностей дитини [5].
- •1. Швидше здібна, ніж обдарована.
- •2. Обдарована.
- •3. Яскрава обдарованість.
- •4. Додаткові ознаки високого творчого потенціалу особистості дитини.
- •1.2. Шкала рейтингу поведінкових характеристик Дж. Рензуллі [5].
- •Шкала I. Пізнавальні характеристики
- •Шкала II. Мотиваційні характеристики
- •Шкала III. Творчі характеристики
- •Шкала IV. Лідерські характеристики
- •1.3. Опитувальник для батьків (і. Шизенко) [5].
- •1.4. Методика „Радощі та засмучення”.
- •1.5. Методика оцінки загальної обдарованості дитини.
- •1.6. Схема діагностики для створення психологічного профілю (г. Россолімо, 1910)
- •1.7. Схема діагностики для виявлення обдарованих дітей (в. Меде і г. Піорковський)
- •1.8. Психографічна схема Штерна, Бааде й Ліпмана
- •Діагностичні вікові шкали а. Біне (1908 і 1911 рр.)
- •1.9. Вікова діагностична шкала о. Бобертага (1912)
- •Вікова діагностична шкала е. Меймана
- •Вікова діагностична шкала л. Термена і г. Чайльдса
- •Іі. Кількісні методики діагностики обдарованості дітей
- •2.1. Методика діагностики обдарованості для педагогів і батьків. Карта інтересів для молодших школярів.
- •2.2. Методика „Карта обдарованості”
- •2.3. Методика експертних оцінок за визначенням обдарованих дітей (а. Лосєва) [5].
- •I. Інтелектуальна сфера.
- •II. Сфера академічних досягнень.
- •III. Творчість.
- •Літературна сфера.
- •V. Артистична сфера.
- •VI. Музична сфера.
- •VII. Технічна сфера.
- •VIII. Рухлива сфера.
- •IX. Сфера художніх досягнень.
- •X. Спілкування й лідерство.
- •2.4. Тестові завдання п. Торренса для діагностики творчої обдарованості
- •2.5. Творче мислення в малюнках
- •Творче мислення в словах Вербальний буклет а
- •Додаток г діагностика дітей „групи ризику” і. Якісні методики діагностики дітей „групи ризику”
- •1.1. Карта обстеження соціально-дезадаптованих неповнолітніх [6].
- •1.2. Показники соціального розвитку підлітка [6].
- •1.3. Карта особистості (може бути використана при діагностиці схильності дітей та підлітків до поведінки, що відхиляється) [6].
- •1.4. Вивчення особистості важкої дитини [7].
- •1. Загальні відомості про дитину.
- •1.5. Анкета для фахівців, педагогів та класних керівників, які працюють з дітьми з девіантною поведінкою [7].
- •1.6. Анкета виявлення девіантної поведінки дітей для батьків [7].
- •1.7. Анкета для дітей та підлітків на виявлення схильності до поведінки, яка відхиляється від норми [7].
- •Іі. Кількісні методи діагностики „дітей групи ризику”
- •2.1. Метод комплексної експрес-діагностики стану соціально-педагогічної занедбаності дітей [6].
- •2.2. Тест схильності до поведінки, що відхиляється від норми (спв) [8].
- •Ключі для підрахунку первинних „сирих” балів
- •2.3. Тест „Оцінка схильності підлітків до азартних ігор”
- •2.3. Експрес-діагностика схильності до адиктної поведінки (в. Бойко) [6].
- •2.4. Експрес-діагностика некерованої емоційної збудливості (в. Бойко) [6].
- •Додоток д діти з функціональними обмеженнями
- •1.1. Методика діагностики батьківського відношення а. Варга, в. Столін
- •1 Шкала : „Прийняття – неприйняття”
- •3. Гра „Рукавички”.
- •4.Гра „Відповідай, сусіде зліва!”
- •5.Міні-лекція „Як виявити аутичну дитину”.
- •6. Гра „Полювання на динозавриків”.
- •7. Міні-лекція „Як допомогти аутичній дитині”.
- •8. Гра „Великий puzzle”.
- •9. Практичне завдання „Робота з поопераційними картами” (робота в підгрупах).
- •10. Міні-лекція „Робота з батьками аутичної дитини”.
- •Література
Міри варіації (мінливості)
Міри центральної тенденції можуть бути корисними соціальному педагогу для узагальнення отриманих у ході вимірів даних, однак це справедливо в тому випадку, коли всі виміри дали близькі або, як кажуть, однорідні чи достатньо гомогенні результати. У тому випадку, коли дані вимірів „розкидані”, міри центральної тенденції погано характеризують варіаційний ряд даних вимірів, їх потрібно використати з зважаючи на міри варіації (мінливості).
Пояснимо це на прикладах.
Припустимо, що два учні написали протягом навчального року по 50 диктантів. Середнє арифметичне число помилок у диктантах кожного з учнів – 0,5. при цьому один з учнів допускав не більше однієї помилки в кожному диктанті, а другий – у диктантах, які йшли після вивчення двох конкретних тем, зробив по 10 помилок. Чи можемо ми на підставі цих даних говорити про те, що обидва учня непогано засвоїли всі правила правопису?
Як видно з цього прикладу, при узагальненні результатів вимірів у ході психолого-педагогічних досліджень аналіз мір центральної тенденції бажано доповнювати аналізом мір варіації.
До мір варіації належать:
розмах (варіаційних розмах);
дисперсія;
стандартне відхилення.
Розмах – це різниця максимального та мінімального значень у варіаційному ряду.
Наприклад: розмах значень 0, 2, 3, 5, 8 дорівнює 8 (8 – 0=0).
Розмах не враховує розподіл всіх значень, крім максимального та мінімального.
Розмах є доволі грубою, але загальнопоширеною мірою мінливості
Дисперсія розраховується за такою формулою:
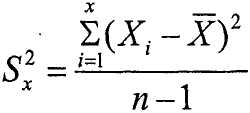
Мірою мінливості, тісно пов’язаної з дисперсією, є стандартне відхилення.
Стандартне відхилення, що позначається s, визначається як позитивне значення квадратного кореня з дисперсії.
На рисунках 8 та 9 представлено графічну інтерпретацію стандартного відхилення. У середньому представники обох груп розв’язали в ході тестування по 10,04 задачі, але стандартне відхилення для групи № 1 (рис. 8) – 0,84, а для групи № 3 (рис. 9) – 6,54.
 Рис.
8. Графічне представлення результатів
тестування в групі № 1 (середнє =
10,04; стандартне відхилення = 0,84)
Рис.
8. Графічне представлення результатів
тестування в групі № 1 (середнє =
10,04; стандартне відхилення = 0,84)
Як видно з рисунків 8 та 9, відносно невелике значення дисперсії (рис. 8) свідчить про „кучність” гомогенність даних. Велике значення дисперсії свідчить про „розкиданість”, неоднорідність отриманих даних.

Рис. 9. графічне представлення результатів тестування в групі № 3 (середнє = 10,04; стандартне відхилення = 6,54).
Кореляційна залежність
Кінцевою метою наукового аналізу, зазвичай, є знаходження зв’язків (залежностей) між змінними. Соціального педагога часто цікавить, як пов’язані між собою дві ознаки, які вивчаються, у цій групі осіб. Наприклад:
Чи мають учні, які навчилися читати раніше за інших, тенденцію до більш високої успішності в старших класах?
Чи є зв’язок між інтелектом батьків та дітей?
Чи будуть робітники з більшим стажем роботи мати більшу продуктивність праці? тощо.
Призначення статистики полягає в тому, щоб допомогти досліднику об’єктивно оцінити залежність між змінними.
За характером зв’язку між змінними можна виділити такі види залежностей.
|
|
|
|
|
|
Ознаки (змінні), які вивчаються в ході психолого-педагогічних досліджень, можуть бути пов’язані функціональною або кореляційною залежністю чи можуть бути ніяк не пов’язані між собою.
Досліднику дуже важливо визначити, чи є якийсь зв’язок між змінними, які вивчаються, і, якщо зв’язок є, з’ясувати, яким є характер цього зв’язку (залежності між змінними).
Функціональна залежність має місце, якщо кожному значенню однієї змінної (Х) відповідає цілком певне значення іншої змінної (Y). На рисунку 15 представлено приклади графічного зображення функціональних залежностей.
Приклади функціональних залежностей:
залежність між швидкістю й пройденою відстанню;
залежність між вартістю й кількістю купленого на певну суму товару;
залежність між загальним стажем роботи й стажем роботи на цьому підприємстві тощо.
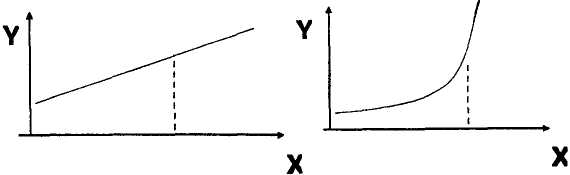
Рис. 15. Приклади графічного зображання функціональних залежностей
Якщо певному значенню однієї змінної відповідає кілька значень іншої змінної, то має місце кореляційна залежність.
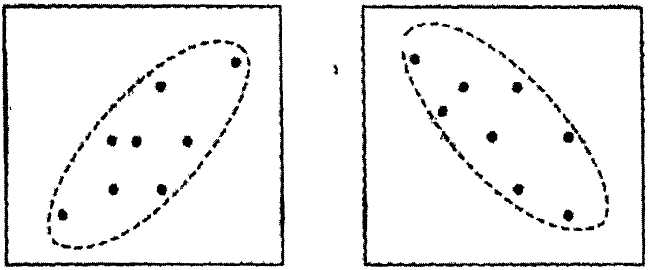
Або, іншими словам, у випадку кореляційної залежності певному значенню однієї величини відповідає комплекс значень іншої, що становить ряд розподілу, при чому, при зміні цієї величини змінюється ряд розподілу та його середнє. Схематичне представлення сили й напрямку кореляції представлено на рисунку 16.
Кореляційний аналіз використовується тоді, коли мета дослідження полягає у знаходженні зв’язку між двома або більш змінними, які спостерігаються у всіх членів вибірки. Завдання кореляційного аналізу – установлення кореляційної залежності між змінними й визначення величини цієї залежності у вигляді коефіцієнтів кореляції.
Коефіцієнти кореляції можуть приймати значення від –1 до +1.
Приклади позитивної кореляції: між IQ та IQ дітей; між ростом батьків та ростом дітей тощо.
Приклади негативної кореляції: між часом, затраченим учнями на перегляд „мильних опер”, та їх оцінками на іспитах.
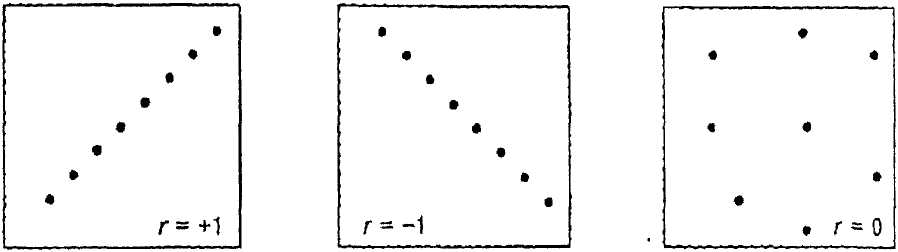
Повна позитивна |
Повна негативна |
Відсутність залежності |
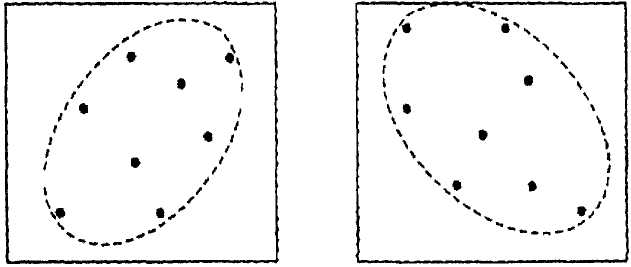
-
r = слабка позитивна
r = слабка негативна
-
сильна позитивна
сильна негативна
Рис. 16. Схематичне представлення сили й напрямку кореляції
Існують два підходи до оцінки сили кореляції. Перший (див. табл. 9) орієнтовано тільки на абсолютну величину коефіцієнта кореляції, а другий – на рівень значущості цього коефіцієнта кореляції при цьому обсязі вибірки (див. табл. 10).
Табл. 9.
