
- •Определение показателя преломления стеклянной плоскопараллельной пластинки при помощи микроскопа Теоретическое обоснование работы
- •Порядок выполнения работы
- •О писание лабораторной установки
- •Порядок выполнения работы
- •I. Определение видимого увеличения микроскопа
- •II. Определение линейного увеличения объектива
- •III. Определение числовой апертуры объектива микроскопа
- •Обработка результатов измерений
- •I. Определение видимого увеличения микроскопа
- •II. Определение линейного увеличения объектива
- •Описание установки и порядок выполнения работы
- •Контрольные вопросы
- •Рекомендуемая литература
- •Измерения с помощью интерференционных колец Ньютона
- •Теоретическое обоснование работы
- •Описание установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Рекомендуемая литература
- •Исследование зависимости коэффициента отражения на границе раздела между двумя диэлектриками от угла падения Теоретическое обоснование работы
- •Описание установки и порядок выполнения работы
- •Подготовка к измерениям
- •Измерения
- •Обработка результатов измерений
- •Закон Малюса
- •Закон Брюстера
- •Описание лабораторной установки
- •I. Экспериментальная проверка закона Малюса
- •II. Определение показателя преломления прозрачного диэлектрика на основе закона Брюстера
- •Обработка результатов измерений
- •I. Экспериментальная проверка закона Малюса
- •II. Определение показателя преломления прозрачного диэлектрика на основе закона Брюстера
- •Контрольные вопросы
- •Рекомендуемая литература
- •Определение концентрации раствора при помощи полутеневого сахариметра Теоретическое обоснование работы и описание установки
- •Закон Малюса
- •Вращение плоскости поляризации раствором естественно-активного вещества
- •Цель работы и ее выполнение
- •Контрольные вопросы
- •Рекомендуемая литература
- •Изучение спектров испускания и поглощения
- •Монохроматор ум-2 и источники излучения
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Дополнительное задание Определение постоянной Планка
- •Порядок определения h
- •Контрольные вопросы
- •Рекомендуемая литература
- •Определение размеров деталей, составляющих хаотическое и упорядоченное множества, с помощью явлений дифракции и интерференции Теоретическое обоснование работы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Рекомендуемая литература
- •Градуировка ширины спектральной щели по дифракционной картине Теоретическое обоснование работы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Рекомендуемая литература
- •Измерение коэффициентов преломления жидкостей и твердых тел
- •Часть I. Измерение показателя преломления жидкости с помощью рефрактометра.
- •Краткие сведения из теории
- •Описание прибора
- •Порядок выполнения работы
- •Обработка и анализ результатов измерений
- •Часть II. Измерение с помощью микроскопа показателя преломления стеклянной плоскопараллельной пластины.
- •Краткие сведения из теории
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка и анализ результатов измерений
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка и анализ результатов измерений
- •Kпогл n λ λ
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка и анализ результатов измерений
- •Контрольные вопросы
- •Рекомендуемая литература
- •Исследование спектров инертных газов
- •Краткие сведения из теории
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка и анализ результатов измерений
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка и анализ результатов измерений
- •Контрольные вопросы
- •Рекомендуемая литература
- •Описание гониометра г1,5
Обработка результатов измерений
Закончив измерения, следует вычислить диаметры (как разность отсчетов N2 - N1), радиусы и квадраты радиусов колец и занести результаты в таблицы 8.1 и 8.2.
Для вычисления значений радиуса кривизны сферической поверхности линзы следует воспользоваться формулой (8.5), комбинируя попарно радиусы следующим образом: 1-8, 2-9, 3-10, 4-11, 5-12, 6-13, 7-14, 8-15. Значение N - М = 7 для всех пар. Результаты вычислений сводятся в таблицу 8.3.
Таблица 8.3
-
№ измерений
пары N - M
λзел
λкр
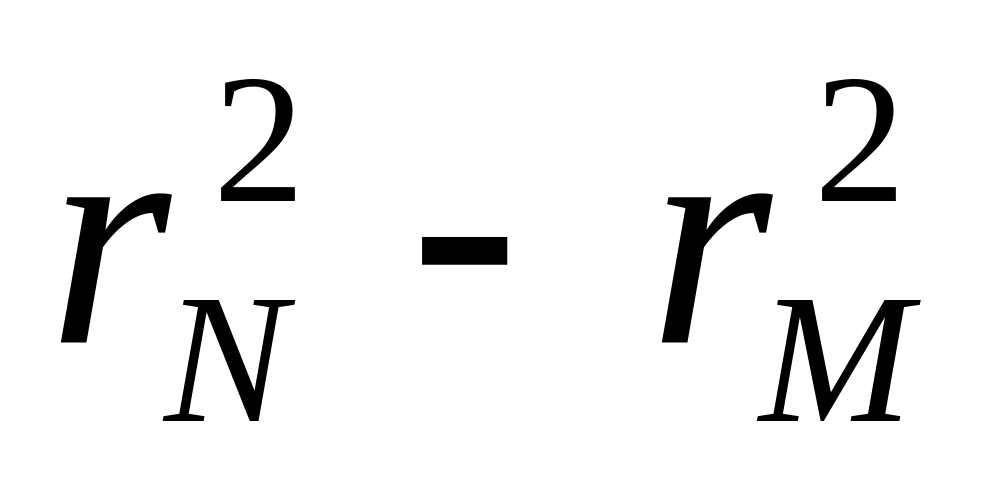 ,
мм2
,
мм2R, мм
, мм2
λ
1
8-1
2
9-2
3
10-3
4
11-4
5
12-5
6
13-6
7
14-7
8
15-8
Среднее значение
Используя полученное значение радиуса кривизны линзы, по формуле (8.6) рассчитываем значения λкр. Результаты расчетов заносятся в таблицу 8.3. Снова для всех пар М - N = 7. Абсолютные погрешности определения R и λкр рассчитываются по разбросу соответствующих величин как погрешности прямых измерений.
Контрольные вопросы
Интерференционные полосы равной толщины. Кольца Ньютона в отраженном и проходящем свете.
Интерференционные полосы равной толщины в случае клина.
Интерференционные полосы равного наклона.
Рекомендуемая литература
Ландсберг Г. С. Оптика. М.: Наука, 1976.
Савельев И. В. Курс общей физики. Изд. 2-е. Т. 3, гл.III. М., Наука, 1970. Изд. 4-е. кн. 4, гл. 4, М., «Наука- Физматмет», 1998.
Яворский Б. М., Детлаф А. А. Курс физики. Т. 3. М., «Высшая школа», 1967.
Калитеевский Н. И. Волновая оптика. Изд. 3-е, гл. 5, М., «Высшая школа», 1995.
Трофимова Т. И. Оптика и атомная физика: законы, проблемы, задачи. Гл. 1, М., «Высшая школа», 1999.
Лабораторная работа №13
Исследование зависимости коэффициента отражения на границе раздела между двумя диэлектриками от угла падения Теоретическое обоснование работы
Отражение света от границы раздела между двумя диэлектриками, например между воздухом и стеклом, описывается формулами Френеля. Введем следующие обозначения:
F0 - падающий световой поток; F1 - отраженный световой поток; r = F1 / F0 - коэффициент отражения; n' - показатель преломления среды, в которую луч входит; n - показатель преломления среды, из которой луч идет; i - угол падения; i' - угол преломления; rs - коэффициент отражения для света, поляризованного в плоскости падения (электрический вектор перпендикулярен лучу и плоскости падения); rр - коэффициент отражения для света, поляризованного перпендикулярно плоскости падения (электрический вектор перпендикулярен лучу и расположен в плоскости падения).
Формулы Френеля имеют следующий вид:
![]() ;
;
![]() (13.1)
(13.1)
Для естественного света, не носящего следов поляризации, полагают, что половина энергии приходится на колебания, перпендикулярные плоскости падения, а половина - на колебания, параллельные плоскости падения. Поэтому коэффициент отражения для естественного света дается выражением
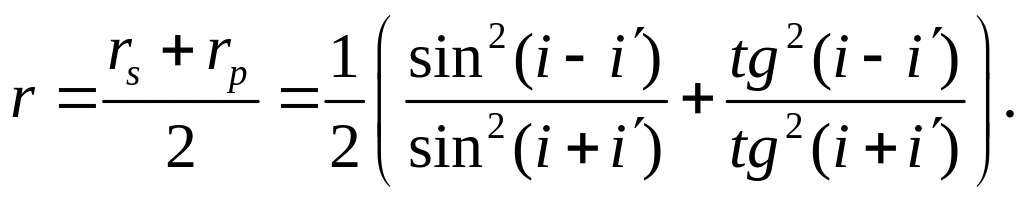 (13.2)
(13.2)
При малых углах падения на границу раздела принимаем sin(i ± i') = i ± i'; tg(i ± i') = i ± i', а закон преломления n sin( i )= n' sin( i' ) можно записать в виде n i = n' i', тогда выражение для r приводится к виду
![]() (13.3)
(13.3)
В работе исследуется зависимость коэффициента отражения стекла в зависимости от величины угла падения в случае, когда луч идет из воздуха (n = 1) в стекло (n' = n). В этом случае формула для коэффициента отражения переписывается.
![]() (13.4)
(13.4)
Кривые зависимостей значений rs, rp и r в функции от угла падения i для случая стекла с nст = 1,52, построенные с помощью формул Френеля, и закона преломления приведены на рис. 13.1. Как следует из графика rs(i), свет с колебаниями электрического вектора, перпендикулярными к плоскости падения, частично отражается при любом угле падения, причем его интенсивность постепенно увеличивается с увеличением угла падения. Из графика rp(i) следует, что для света с колебаниями, лежащими в плоскости падения, при угле падения равном 56°40' для стекла с n = 1,52, коэффициент отражения равен 0, то есть свет не отражается. При больших углах отражение вновь имеет место.
Из рассмотрения хода кривых
рис. 13.1 ясно, что при падении естественного
луча на такое стекло под углом 56°40' в
отраженном луче останутся только
колебания электрического вектора,
перпендикулярные плоскости падения.
Отраженный луч будет полностью линейно
поляризован (рис. 13.2)
rs,
r, rp
iº
Рис 13.1

У
n
n´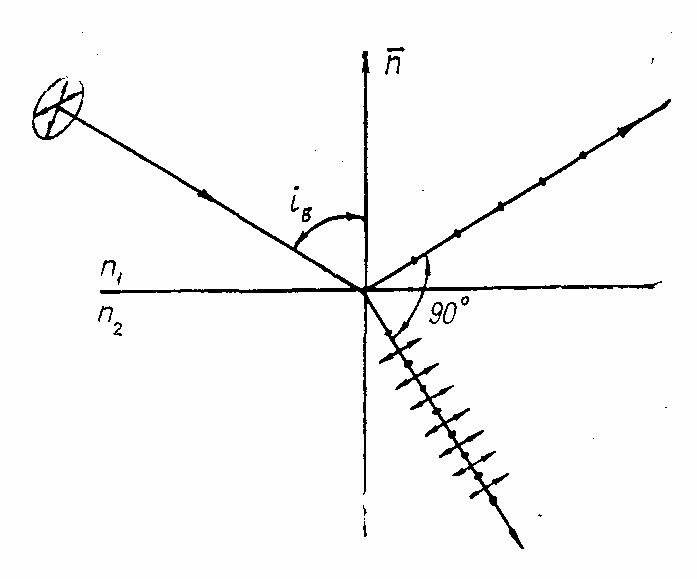 гол
падения, при котором отраженный луч
оказывается полностью линейно
поляризованным, называется углом полной
поляризации или утлом Брюстера. Можно
показать, что тангенс угла полной
поляризации
гол
падения, при котором отраженный луч
оказывается полностью линейно
поляризованным, называется углом полной
поляризации или утлом Брюстера. Можно
показать, что тангенс угла полной
поляризации
Рис 13.2![]()
При этом преломленный луч остается частично поляризованным с преимущественным направлением колебания электрического вектора в плоскости падения
Целью работы является:
Определение коэффициентов отражения rs и rр в зависимости от угла падения i.
Вычисление коэффициента отражения r = r(i) на основании измеренных значений rs = rs(i) и rp = rp(i).
Определение значения угла Брюстера с помощью графика rp = rp(i) и вычисление показателя преломления данного стекла.
Сопоставление значений nст, вычисленных по формуле Брюстера и по формуле Френеля (для малых углов падения i).
Сопоставление некоторых экспериментальных результатов со значениями вычисленными по формулам Френеля.
