II. Определение линейного увеличения объектива

1. Надеть винтовой окуляр-микрометр.

2. С помощью винтового окуляр-микрометра измерить размер изображения стороны сетки Горяева (b) (не менее 5 раз). Результаты измерений занести в табл. 3.2. (инструкция по использованию винтового окуляр-микрометра- на рабочем столе)

3. Сетку Горяева и винтовой окуляр- микрометр снять.

Результаты измерений занести в табл. 3.2. Вычислить погрешность в определении значения .

Таблица 3.2

№ измерении	Измеряемая величина
	b, мм	b - bср, мм	(b - bср)2, мм2
1
2
3
4
5
Среднее значение

III. Определение числовой апертуры объектива микроскопа

1. Вставить окуляр в микроскоп.

2. Положить пластинку П с малым отверстием на предметный столик микроскопа.

3. Сфокусировать микроскоп на резкое видение малого отверстия в пластинке П.

4. Удалить окуляр из микроскопа и надеть на тубус колпачок К с малым отверстием.

5. Положить на зеркало микроскопа лист миллиметровой бумаги.

6. С осчитать число клеток мм, у мещающихся в поле зрения. Результаты измерений занести в табл. 3.3.

Рис 3.6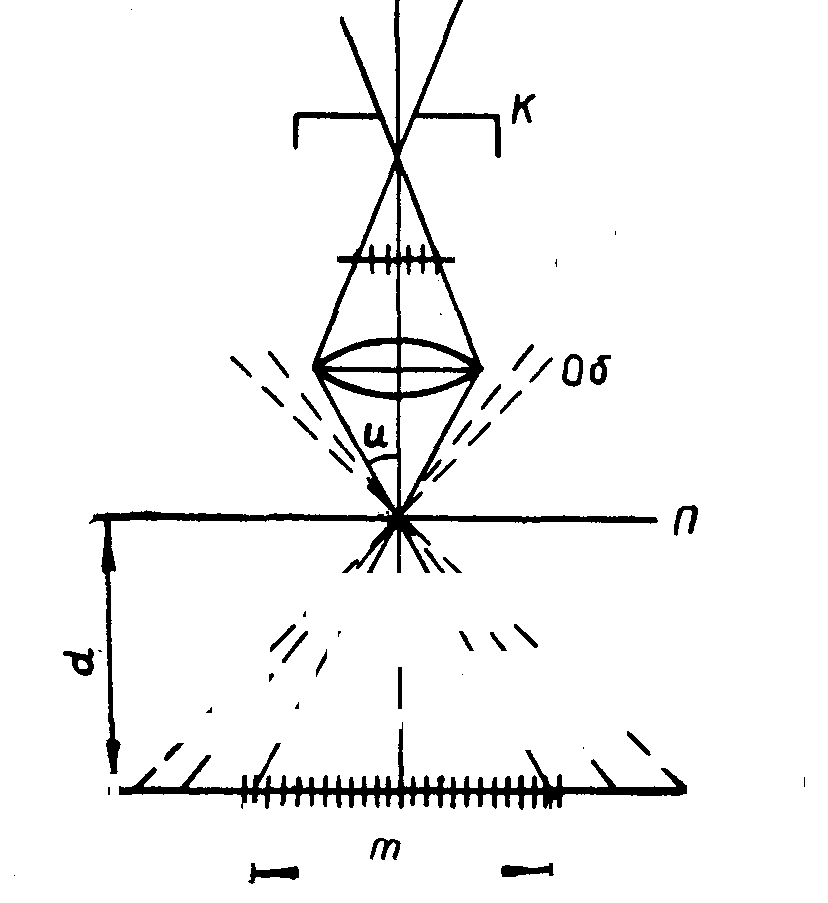

Таблица 3.3

№ измерений	Измеряемая величина
	m, мм	m - mср, мм	(m - mср)2, мм2
1
2
3
4
5
Среднее значение

Примечание: m измеряют с точностью до половины деления.

Обработка результатов измерений

I. Определение видимого увеличения микроскопа

1. Рассчитать видимое увеличение микроскопа Г по формуле

(3.2)

где а' - размер изображения стороны маленькой клетки сетки Горяева; а - истинный размер стороны маленькой клетки сетки Горяева (указан на сетке Горяева).

2. Вычислить погрешность полученного результата.

II. Определение линейного увеличения объектива

1. Рабочая формула для определения увеличения объектива представлена в виде

(3.3)

где b - размер изображения стороны клетки сетки Горяева, измеренный окулярным микрометром; а - истинный размер ее стороны; =160 мм - оптическая длина тубуса микроскопа; = 192 мм - оптическая длина тубуса микроскопа с винтовым окулярным микрометром.

2. Вычислить погрешность.

3. Зная видимое увеличение микроскопа Г и линейное увеличение объектива , вычислить видимое увеличение окуляра по формуле (3.1).

4. Найти погрешность результата.

III. Определение числовой апертуры объектива микроскопа

1. Найти значение

(3.4)

2. По tgu найти искомую величину A = n·sinu.

3. Вычислить погрешность полученного значения числовой апертуры А.

4. Сопоставить результат непосредственного измерения числовой апертуры с номинальным значением, указанным на объективе микроскопа.

Контрольные вопросы

1. Видимое увеличение оптических приборов.

2. Ход лучей в лупе и микроскопе.

3. Разрешающая сила и полезное увеличение микроскопа.

Рекомендуемая литература

1. Савельев И.В. «Курс общей физики». Изд. 4-е, кн. 5, гл. 5, §§ 5.2, 5.13. М., «Наука - Физматлит», 1998г.

2. Ландсберг Г. С. Оптика. Изд. 4-е, Главы XXII и XXIII. М., Гостехиздат, 1957.

3. Фриш С. Э., Тиморева А. В. Курс общей физики. Т. 3. гл. XXVIII. М., Физматгиз, 1962

Лабораторная работа №7

Определение длины световой волны при помощи бипризмы

Теоретическое обоснование работы

Расчет интерференционной картины на экране от двух когерентных источников света. Пусть S₁ и S₂ - два когерентных источника света с длиной волны λ, (рис. 7.1), расположенные на расстоянии l друг от друга. На расстоянии d₀ от них расположен экран Э. Зададимся произвольной точкой на экране, координата которой у. Будем рассматривать точки экрана, для которых у << d₀.

Пусть разность хода между лучами, пришедшими от когерентных источников в данную точку экрана, представляется отрезком δ. Из рис. 7.1 видно, что поскольку можно принять tgφ sinφ φ, имеет место . Отсюда , т.е. разность хода лучей для различных точек экрана есть функция координаты у. В точках экрана, для которых , имеют место максимумы интенсивности, в точках экрана, для которых , минимумы интенсивности.

Т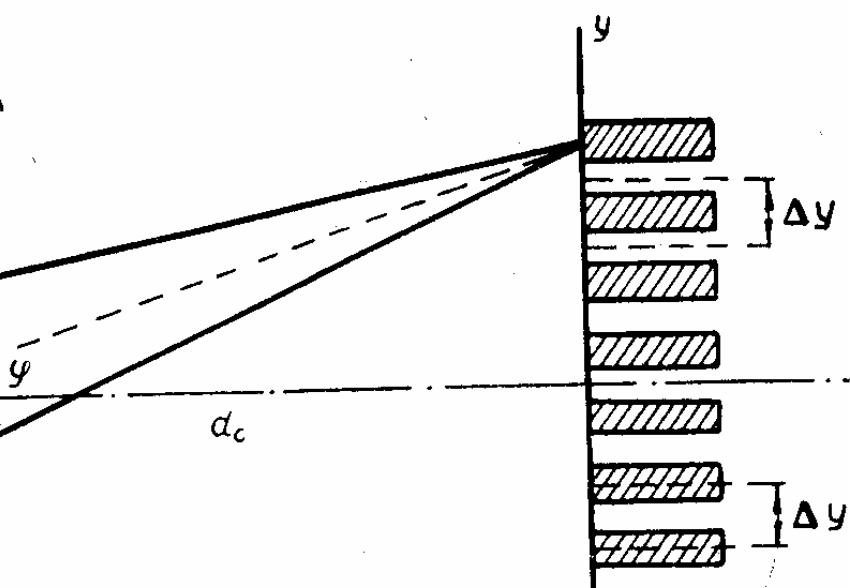 аким образом, для света с длиной волны интерференционная картина на экране представляет собой чередующиеся светл ые и темные полосы, перпендикулярные плоскости чертежа.

П оложение k-го максимума (k - порядок и нт ерференции) определяется из уравнения

а положение k-го минимума - из уравнения

.

Здесь k = 0, 1, 2, 3, ...

Ш

Рис 7.1

ириной полосы называют расстояние между осями двух соседних максимумов или минимумов. Из выражения для y_kmax и у_kmin следует, что ширина полосы Δу равна

Δу = у_(k+1)max - y_kmax = y_(k+1)min - y_kmin =λ . Исходя из этой формулы, можно определить длину волны λ

λ = (7.1)

В работе для получения двух когерентных источников используется бипризма Френеля. Бипризма представляет собой две призмы с малыми преломляющими углами, сложенные основаниями. Падающий от щели пучок света (щель перпендикулярна плоскости чертежа) после преломления в бипризме разделится на два перекрывающихся пучка, исходящих из двух мнимых изображений щели S₁ и S₂ (рис. 7.2).

Легко убедиться в том, что расстояние между мнимыми источниками S₁ и S₂ равно

l = 2r (n - 1) α.

З десь r - расстояние от источника до бипризмы; n - показатель преломления вещества бипризмы; α - преломляющий угол каждой половинки бипризмы.

В пространстве за бипризмой будет наблюдаться интерференционная картина в любой плоскости, пересекающей лучи в заштрихованной области в виде чередующихся темных и светлых полос (полосы изображены на рис. 7.2 и перпендикулярны плоскости чертежа).