Обработка и анализ результатов измерений

1. Найти значение на основе формулы (74.3). Для этого найти по полученным экспериментальным данным значения в окрестности = 45°, которым соответствуют значения 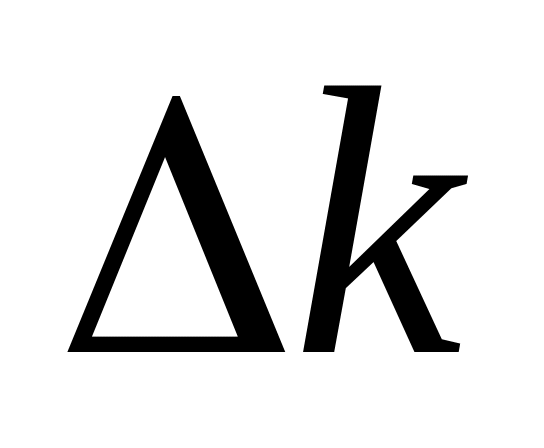= 10 и 20 (ближайшие две серии по десять интерференционных полос по разные стороны от 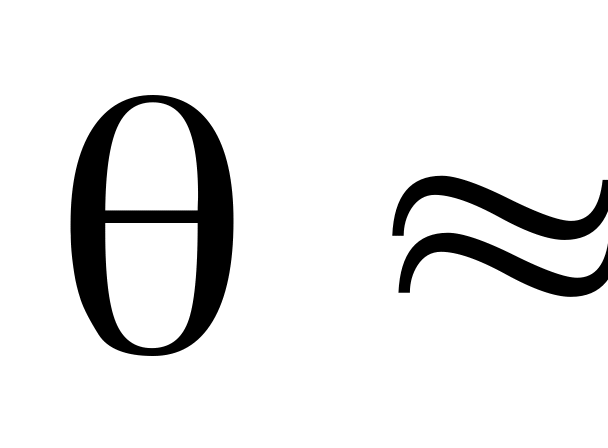45°). Для расчетов взять среднее из четырех определений . Здесь диаметр диска D = (20,00 ± 0,01) мм, длина волны излучения лазера указана на установке.

2. Вычислить = f ( ) по формуле (74.2). Результаты расчетов занести в табл. 74.2. Построить по этим данным график зависимости = f ( ).

Таблица 74.2

	sin

3. Вычислить значения = f ( ) по измеренным данным, пользуясь формулой (74.4). Результаты расчетов занести в табл. 74.1.

4. Нанести на график, построенный по формуле (74.2), экспериментальные точки, полученные с помощью формулы (74.4). Сопоставить графики зависимости = f ( ), полученные экспериментально и по формуле (74.2). Сделать, выводы из этого сопоставления.

5. По разбросу значений 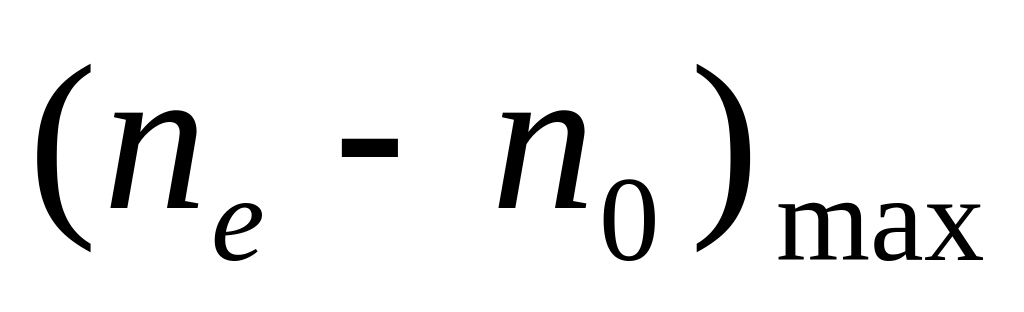определить погрешность измерений.

Контрольные вопросы

1. Объяснить явление вращения плоскости поляризации при прохождении луча в одноосном монокристалле вдоль оптической оси.

2. Как осуществить интерференцию поляризованных лучей?

3. В чем заключается явление двойного лучепреломления в одноосном монокристалле?

4. Каковы физические основы работы газовых лазеров?

Рекомендуемая литература

1. Савельев И. В. Курс общей физики. Изд. 4-е. кн. 4, гл. 6. М., «Наука- Физматлит», 1998.

2. Трофимова Т. И. Оптика и атомная физика: законы, проблемы, задачи. Гл. 3. М., «Высшая школа», 1999.

Лабораторная работа № 76

Изучение дисперсии света

Цели работы: определение показателя преломления n вещества призмы для различных длин волн λ методом призмы; построение кривой зависимости этого показателя от длины волны света; определение дисперсии вещества D = (dn) / (dλ) и построение кривой дисперсии D = f(λ); а также определение фазовой и групповой скорости света в стекле.

Краткие сведения из теории

Свет - это электромагнитная волна больших частот. Частоты видимого излучения лежат в диапазоне (0,75 0,39)10¹⁵ с^-1, что соответствует длинам волн λ = (400 760) нм. Скорость света в вакууме для всех частот одинакова и равна с = м/с.

В веществе фазовая скорость света зависит от частоты. Абсолютный показатель преломления вещества равен отношению скорости света в вакууме к фазовой скорости света в веществе:

n = с / υ. (76.1)

Следовательно, показатель преломления вещества зависит от частоты или от длины волны λ (λ = с/ν) в вакууме: n = f(λ). Явление зависимости фазовой скорости и показателя преломления от длины световой волны называется дисперсией света. Если в веществе для длины волны λ показатель преломления n, то для λ + dλ он станет равным n + dn, т. е. dn ~ dλ и можно записать: dn = Ddλ, где D - коэффициент дисперсии вещества или просто дисперсия вещества: D = (dn)/(dλ). Этот коэффициент показывает быстроту изменения показателя преломления вещества при изменении длины волны.

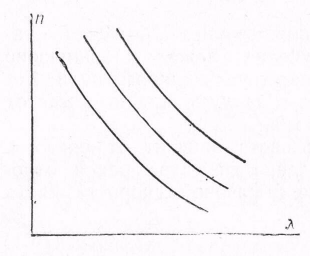
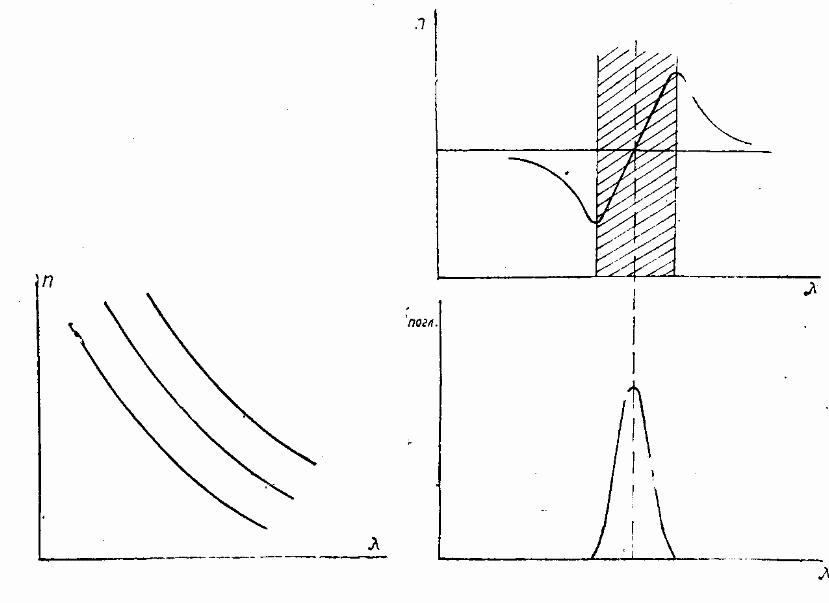
Для каждого вещества существуют области нормальной дисперсии, в которых с возрастанием длины волны показатель преломления убывает, т. е. D < 0. Изменения n в этой области происходят не скачком, а плавно. На рис. 76.1 показаны области нормальной дисперсии для трех разных веществ, отличающихся показателем преломления. Все вещества имеют полосы поглощения электромагнитных волн. Область нормальной дисперсии наблюдается в веществах для длин волн, далеких от полос поглощения.

Прозрачное, неокрашенное стекло имеет две полосы поглощения: вблизи λ₁ = 2 мкм (инфракрасная область) и λ₂ = 0,36 мкм (ультрафиолетовая область), т. е. в видимой части спектра в таком стекле наблюдается только нормальная дисперсия. При приближении к области поглощения со стороны малых длин волн коэффициент преломления с возрастанием λ сначала скачком уменьшается, а при переходе через полосу поглощения резко возрастает, достигая максимума. Эта особенность в ходе дисперсионной кривой n = f (λ) получила название аномальной дисперсии. На рис. 76.2 изображены кривая аномальной дисперсии и зависимость коэффициента поглощения k_погл вещества от λ. В области аномальной дисперсии D > 0. Явление дисперсии объясняется электронной теорией дисперсии [3, 4].

Немонохроматическая волна в веществе вследствие дисперсии расплывается, так как каждая ее составляющая распространяется со своей фазовой скоростью. Скорость распространения общего максимума группы волн (или скорость распространения сигнала) называется групповой скоростью, она равна:

n

Рис. 76.1