Обработка результатов измерений

1. По данным таблицы построить градуировочный график l = f(λ) (на миллиметровой бумаге), используя известный линейчатый спектр паров ртути.

2. Пользуясь градуировочным графиком, определить длины волн спектральных линий исследуемого неизвестного газа. Результаты занести в таблицу.

3. Оценить погрешность.

Дополнительное задание Определение постоянной Планка

Под действием света могут происходить различные химические реакции. Например, разложение иона , входящего в состав водного раствора , описывается уравнением

Каждому поглощенному кванту света соответствует разложение одной поглотившей свет молекулы (иона). Вызвать разложение могут только те кванты, энергия которых не меньше Е₁, необходимой для разложения молекулы, т.е. удовлетворяющие условию . Следовательно, квант света с длиной волны , еще способной вызвать распад иона, удовлетворяет условию

(18.1)

где = 22,3·10⁷ дж/кмоль (для нашего раствора) - энергия, необходимая для разложения киломоля ионов ;

N₀ = 6,024·10²⁶ 1/кмоль - число Авогадро;

с = 3·10⁸ м/сек- скорость распространения света в вакууме.

Тогда постоянная Планка определяется из уравнения (18.1)

(18.2)

Порядок определения h

Щель спектрометра освещается лампой накаливания. Между щелью и лампой помещают кювету с раствором По шкале спектрометра определяется граница полосы поглощения (со стороны длинных волн) и по градуировочной кривой прибора , где l - деления шкалы спектрометра, определяют . Тогда постоянную Планка определяют по формуле (18.2). Определение следует выполнить пять раз и найти абсолютную ошибку по разбросу значений . Значение Q берем с ошибкой в единицу разряда последней значащей цифры

Вычисляем относительную и абсолютную ошибки определения h и записываем результат в следующем виде

Следует соблюдать осторожность при обращении с раствором, не допуская его разбрызгивания и попадания на руки и одежду.

Контрольные вопросы

1. Различие между дифракционным и призматическим спектром.

2. Дисперсия призмы и дисперсия вещества призмы.

3. Виды спектров. Спектральный анализ.

4. Ход лучей в призматическом спектрографе.

Рекомендуемая литература

1. Савельев И.В. Курс общей физики. Изд. 4-е, кн. 4, гл. 7; кн. 5, гл. 5. М., «Наука - Физматлит», 1998г.

2. Яворский Б. М., Детлаф А. А. Курс общей физики: Т. 3, гл. VII. М., «Высшая школа», 1965г.

3. Ландсберг Г. С. Оптика. М., Наука, 1967.

4. Трофимова Т.И. «Оптика и атомная физика: законы, проблемы, задачи». Гл. 4, 8 и 9. М., «Высшая школа», 1999г.

5. Путилов К. А. Фабрикант В. А. Курс физики. Т. 3, гл. VI. М., Физматгиз, 1963.

Лабораторная работа № 20

Определение размеров деталей, составляющих хаотическое и упорядоченное множества, с помощью явлений дифракции и интерференции Теоретическое обоснование работы

В случае дифракции Фраунгофера дифракционные картины на удаленном экране (или в главной фокальной плоскости линзы) от одной частицы и от хаотического множества тождественных частиц одинаковы по своему строению и различаются лишь по интенсивности. Это справедливо и в случае освещения хаотического множества частиц когерентным излучением, поскольку хаотичность в расположении частиц устраняет интерференцию при наложении дифракционных картин от различных частиц. Большая интенсивность максимумов дифракционной картины от хаотического множества сравнительно с картиной от одной частицы позволяет удобно наблюдать и измерять положение дифракционных максимумов (гало) и минимумов. Необходимым условием наблюдения гало является то, что размеры деталей, дающих дифракцию, должны превышать длину волны используемого света. Поэтому галографическое исследование формы и размеров микрочастиц (атомы, молекулы) требует использования рентгеновского излучения с длиной волны порядка долей ангстрема. Для определения размеров и формы частиц с протяженностью порядка нескольких микрон может быть использован свет видимого диапазона путем измерений размеров видимых гало.

В случае упорядоченного расположения множества тождественных деталей при использовании когерентного излучения на дифракционную картину от одной детали налагается картина интерференции, из измерений которой можно определить период структуры из упорядоченных деталей.

В работе в качестве хаотического множества частиц используются частицы ликоподия, заключенные между двумя стеклянными пластинками. Эти частицы имеют шарообразную форму, и поэтому галограмма от них, наблюдаемая на экране при просвечивании пластины с ликоподием таким пучком, представляет собой концентрические кольца.

В качестве упорядоченной структуры в работе берется множество параллельных щелей, расположенных на одинаковых расстояниях друг от друга (дифракционная решетка). Каждая щель в направлении, перпендикулярном ей, образует дифракционную картину на экране. От упорядоченного множества щелей на дифракционную картину налагается картина интерференции. Благодаря тому, что длина щели значительно больше ширины, дифракционная картина одномерная.

Если упорядоченная структура имеет решетчатое строение со сравнимыми по величине сторонами элементов структуры (например, две скрещенные решетки), то интерференционная картина имеет двухмерное дискретное строение, которое налагается на дифракционные гало, соответствующие одной форме ячейки. Из измерений интерференционной картины можно определить период двухмерной структуры.

В работе используется тонкий пучок параллельных лучей (луч), получаемый от лазера.

Преимущества лазерного луча перед любым другим световым излучением заключаются в высокой когерентности, большой интенсивности и малой расходимости. Благодаря этим качествам можно на удаленном экране наблюдать гало от хаотической структуры микрочастиц, а в случае упорядоченной структуры наблюдать на экране интерференцию высоких порядков. Это обеспечивает достаточно малую относительную погрешность измерений при использовании сравнительно грубых способов измерений линейных величин.

Содержание данной работы заключается в следующем:

1. Определение диаметров частиц (шариков) ликоподия по галограмме, получаемой на экране при просвечивании пластинки с хаотическим множеством частиц.

2. Определение периода упорядоченной одномерной структуры из параллельных друг другу щелей, расположенных на одинаковых расстояниях друг от друга, по интерференционной картине, наблюдаемой на экране при просвечивании лучом лазера этой структуры.

3. Определение периодов двухмерной упорядоченной структуры с взаимно перпендикулярными сторонами тем же способом.

Первая часть работы выполняется на основе выражения для радиусов минимумов освещенности в дифракционной картине от круглого экрана (по принципу Бабине дифракционные картины от круглого отверстия или экрана одинаковы за исключением центральных частей картины).

Это выражение имеет вид:

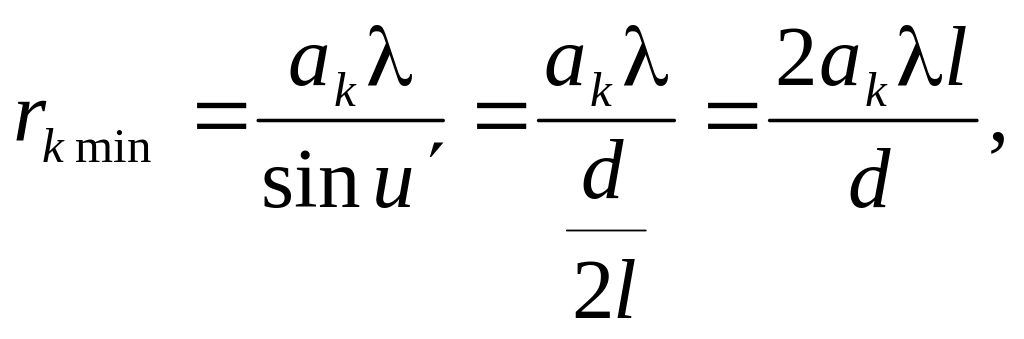k =1,2,3.... (20.1)

откуда диаметр частицы

. (20.2)

С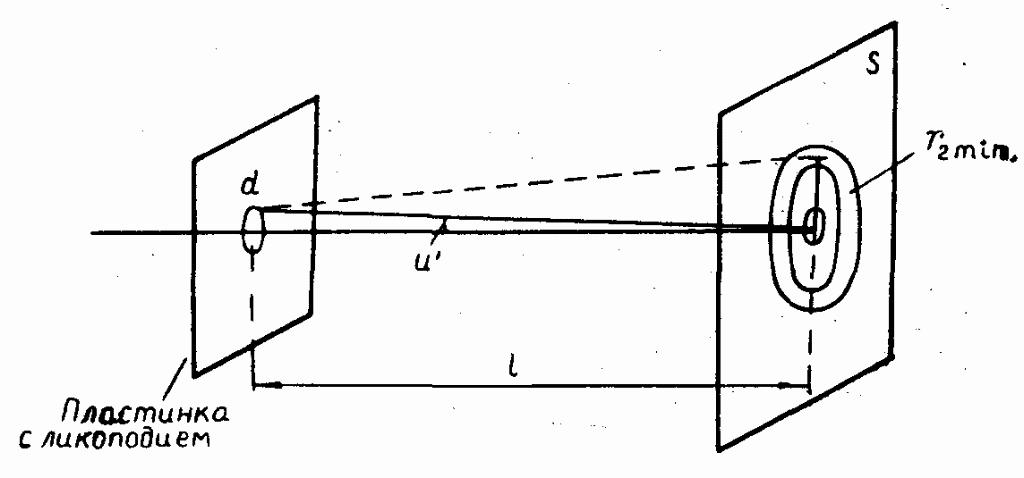 мысл обозначений виден из рис. 20.1. Здесь d - диаметр частицы ликоподия; l - расстояние от частицы ликоподия до экрана S; u' - апертурный угол, стягиваемый радиусом частицы, с вершиной в точке О экрана S; λ - длина волны излучения лазера, а_k принимает следующие значения для радиусов r_kmin: a₁ = 0,61, а₂ = 1,12, a₃ = 1,62.

r_2min

r_1min

Пластинка с ликоподием

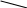
В

Рис. 20.1

торая часть работы выполняется на основе выражения, определяющего положение главных максимумов интерференционной картины от дифракционной решетки, с периодом d. При нормальном падении лучей это выражение имеет вид

k = 0, 1, 2,...

Учитывая, что расстояние от дифракционной решетки до экрана велико по сравнению с расстоянием от нулевого максимума до используемых максимумов k-го порядка (у_kmax, рис. 20.2), можно положить

Тогда значение периода решетки d определяется уравнением

(20.3)

Значение y_kmax можно принять по тем же причинам равным

Тогда выражение (20.3) переписывается

(20.4)

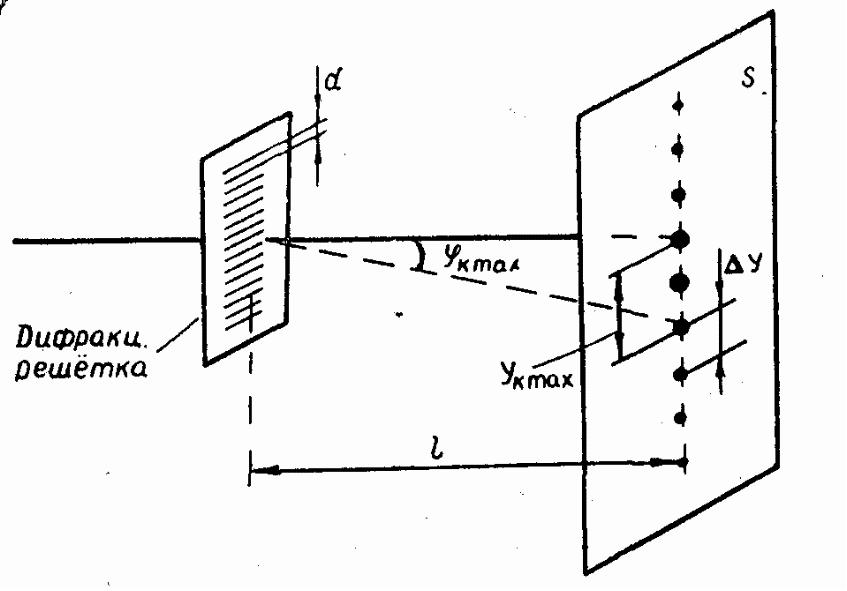
Д

Рис. 20.2

ля выполнения третьей части работы используется решетка 2, состоящая из двух решеток, щели которых взаимно перпендикулярны. При этом на экране S наблюдается интерференционная картина, возникшая от наложения дифракционных картин от каждой из решеток. 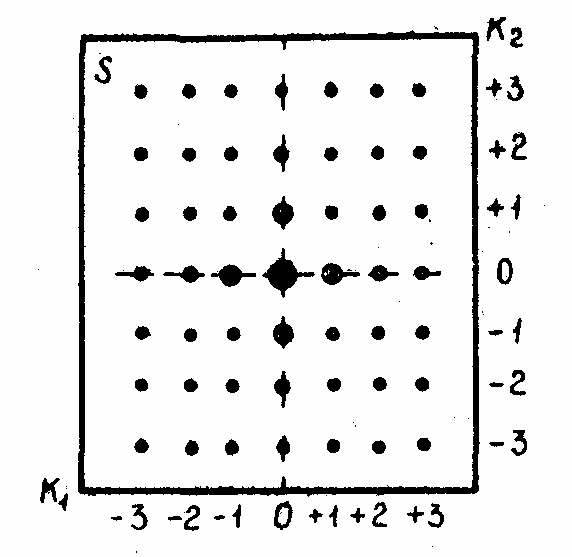Она имеет вид дискретных прямоугольников, и периоды обеих решеток получаются путем измерений интерференционной, картины в двух взаимно перпендикулярных н аправлениях вдоль осей симметрии. На рис. 20.3 показана картина, наблюдаемая на экране S. Максимумы показаны кружочками, размеры которых характеризуют интенсивности.

Рис. 20.3