Лабораторная работа №1 Тема: «Создание математических моделей динамических систем в пакете Matlab»

Цель работы: Получение навыков исследования динамических систем с использованием цифровых моделей.

Задачи:

1. Освоить систему визуального моделирования Simulink;

2. Создать модель динамической системы;

3. Провести анализ результатов моделирования.

1. Теоретические сведения

Одной из важных научных проблем является решение задачи предсказания поведения изучаемого объекта во времени и пространстве на основе определенных знаний о его начальном состоянии. Эта задача сводится к нахождению некоторого закона, который позволяет по имеющейся информации об объекте в начальный момент времени t₀ в точке пространства x₀ определить его будущее в любой момент времени t > t₀. В зависимости от степени сложности самого объекта этот закон может быть детерминированным либо вероятностным, может описывать эволюцию объекта только во времени, только в пространстве, либо пространственно-временную эволюцию.

Под динамической системой понимают любой объект или процесс, для которого однозначно определено понятие состояния как совокупности некоторых величин в данный момент времени и задан закон, который описывает изменение (эволюцию) начального состояния с течением времени. Этот закон позволяет по начальному состоянию прогнозировать будущее состояние динамической системы.

Таким образом, динамическая система – это математическая абстракция, предназначенная для описания и изучения систем, эволюционирующих с течением времени. Примерами динамических систем могут служить механические, физические, химические и биологические объекты, вычислительные процессы и процессы преобразования информации, совершаемые в соответствии с конкретными алгоритмами и другие явления и процессы.

Описания динамических систем для задания закона эволюции также разнообразны: с помощью дифференциальных уравнений, дискретных отображений, теории графов, теории Марковских цепей и т.д. Выбор конкретного способа описания задает вид математической модели соответствующей динамической системы.

Исследование реальных систем сводится к изучению математических моделей, совершенствование и развитие которых определяются анализом экспериментальных и теоретических результатов при их сопоставлении.

В качестве инструмента в данной лабораторной работе используется Simulink – среда имитационного моделирования, являющаяся приложением к пакету MATLAB. Модели в Simulink строятся с помощью стандартных блоков, и в общем случае включают источники сигналов, их преобразователи, а также средства визуального представления и анализа данных. Важным достоинством моделей Simulink является их связь с математическим ядром MATLAB и, следовательно, возможность тонкой настройки параметров блоков.

За счет своей наглядности и относительной простоты создания моделей данное средство нашло применения при решении широкого круга задач, в первую очередь связанных с моделированием систем и средств обработки сигналов. В лабораторной работе рассматривается способ описания динамической системы дифференциальными уравнениями и их решение с помощью Simulink. Основной принцип, используемый при решении систем дифференциальных уравнений, заключается в последовательном интегрировании.

В качестве примера рассмотрим следующее дифференциальное уравнение, разрешенное относительно старшей производной:

. (1)

На рисунке 1.1 приведена модель, реализованная в пакете Simulink для решения данного дифференциального уравнения. В модели использованы блоки математических функций и интеграторов. Основу модели составляет сумматор, на вход которого подаются сигналы, соответствующие искомой функции, ее первой производной а также дополнительным слагаемым (правая часть уравнения). С выхода сумматора снимается сигнал, соответствующий второй производной (левая часть уравнения). Переменная t, линейно изменяющаяся с течением времени задаются при помощи блока Clock (Часы). Начальные условия y(0) и y’(0) задаются в блоках интеграторов.

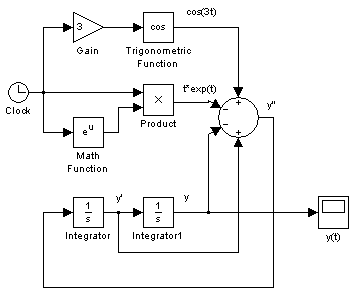
Рис. 1.1 – Модель в пакете Simulink для решения дифференциального уравнения (1).

На рисунке 1.2 приведен результат решения данного дифференциального уравнения – график функции y(t), снимаемый с блока Scope.

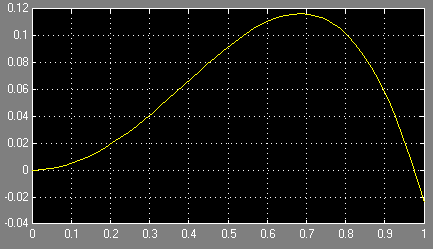
Рис. 1.2 – Результат решения дифференциального уравнения (1)

Таким образом, данный подход позволяет получить численное решение сложных дифференциальных уравнений, аналитическое решение которых затруднено либо невозможно.

1.2 Описание проблемы и постановка задачи

Рассмотрим файлообменную сеть, имеющую топологию точка-точка и состоящую из M узлов (см. рис. 1.3). Каждый из пользователей сети желает получить копию распространяемого файла. Кроме того, в сети действуют N злоумышленников, которые под видом полезной информации распространяют поврежденные (зараженные вирусами или червями) версии файлов. Внешне (имя, тип, размер файла) они не отличаются от полезных, и определить это можно только скачав файл.

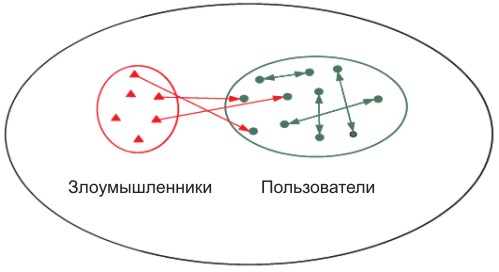
Рис. 1.3 – Общий вид файлообменной сети.

Передача информации начинается после того, как один из пользователей делает доступной для других свою версию файла. Одновременно (либо заранее), злоумышленник выкладывает испорченную версию. Таким образом, новые пользователи могут выбрать из списка предложенных файлов испорченный – с вероятностью p, либо полезный – с вероятностью (1 – p) (см. рис. 1.4).

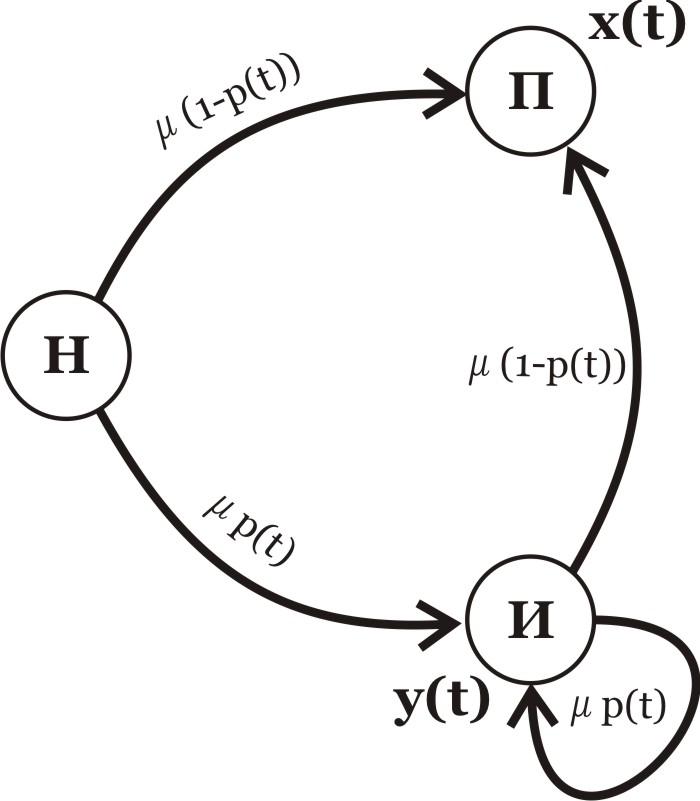
Рис. 1.4 – Граф состояний системы

Скачав новый файл, пользователи проверяют его не сразу, а через некоторое время 1/μ. В случае, если файл поврежден, он удаляется и поиск начинается заново. До тех пор, он остается доступным для скачивания другими пользователями. Предположим, что время передачи пренебрежимо мало по сравнению с интервалами между проверками. Такое допущение возможно в современных сетях с широкополосным доступом при передаче небольших файлов (например, музыки в формате MP3), либо при передаче больших объемов информации с разбивкой на части.

Таким образом, каждый из M пользователей сети в любой момент времени, может быть отнесен к одной из следующих категорий:

- пользователи, имеющие полезную версию файла (П), обозначим их количество x(t);

- пользователи, имеющие испорченную версию файла (И), количеством y(t);

- новые пользователи, не имеющие никакой версии (Н), количеством (M – x(t) – y(t)).

Будем рассматривать функции x(t) и y(t), как непрерывные. Вероятность скачивания пользователем испорченной версии файла в любой момент времени определяется выражением:

. (2)

Количество копий полезного файла x(t) увеличивается, когда пользователь, не имеющий файла, скачивает полезную версию, что происходит со скоростью:

, (3)

либо когда полезную версию скачивает пользователь, скачавший до этого испорченный файл, что происходит со скоростью:

. (4)

Аналогично, количество испорченных копий увеличивается, когда новые пользователи скачивают испорченный файл со скоростью:

. (5)

Однако, оно уменьшается при скачивании полезного файла, пользователем, скачавшим до этого испорченную версию:

. (6)

С учетом этого, поведение динамической системы, которую представляет собой сеть, может быть описано с помощью системы нелинейных дифференциальных уравнений:

; (7)

.

После преобразований получим:

; (8)

.

Предположим, что общее количество пользователей в сети изменяется по некоторому закону M(t). Пусть, также, пользователи, имеющие полезную версию файла, прекращают раздачу (покидают сеть) со скоростью α, а пользователи, скачавшие испорченную версию файла – со скоростью β. С учетом этого, система уравнений примет вид:

; (9)

.

Пусть количество пользователей изменяется по закону:

. (10)

Решив полученную систему уравнений можно определить состояние сети в любой момент времени t.