1 Общие сведения

В ходе проведения реформ в Российской Федерации значительно возросли объемы землеустроительных и кадастровых работ. Это требует повышения производительности труда, а также улучшения качества их проведения.

Научные исследования и практика показали, что для принятия управленческих и организационно-хозяйственных решений целесообразно шире использовать математический аппарат, в том числе экономико-математические методы.

Экономико-математические методы и моделирование начали применяться в землеустройстве с начала 60-тых годов прошлого века.

Их развитие можно разделить на три этапа.

Первый этап длился с начала 60-тых годов до конца 70-тых годов. В этот период была обоснована необходимость и сформулированы задачи.

Преподавание экономико-математических методов было начато в 1964 году Московском институте землеустройства.

В 1988 году этот курс трансформировался в дисциплину «Экономико-математические методы и моделирование».

На первом этапе в основном решались задачи внутрихозяйственного землеустройства.

Второй этап относится к 80-тым годам. Он связан с обоснованием и созданием автоматизированных систем плановых расчетов, систем автоматизированного проектирования (САПР) и автоматизированных рабочих мест (АРМ).

Третий этап начался в 90-тые годы. В этот период произошло полное техническое перевооружение землеустроительной службы страны, её оснащение отечественной и зарубежной вычислительной техникой. Получили интенсивное развитие географические информационные системы (ГИС) и земельно-информационные системы (ЗИС).

2 Статистическая обработка информации

Статистические данные представляют собой наблюдаемые или измеряемые значения одного или нескольких признаков обследуемой совокупности объектов. Различают количественные и качественные признаки. Значения количественных признаков могут быть непрерывными или дискретными. Качественные признаки в зависимости от вида данных делятся на номинальные и ординальные.

Множество всех обследуемых объектов называется генеральной совокупностью. Если это множество содержит небольшое число элементов, то возможно полное обследование всех его элементов. Однако в большинстве случаев в силу того, что генеральная совокупность имеет очень много элементов либо её элементы труднодоступны, либо по другим причинам обследуется некоторая часть генеральной совокупности – выборка. В этом случае основные характеристики генеральной совокупности оцениваются (то есть определяются приближенно) по выборке. Соответствующие статистики называются «выборочное среднее», «выборочная дисперсия» и т. д. Очевидно, что не всякая выборка правильно отражает свойства генеральной совокупности. Например, нельзя судить о среднем душевом доходе населения по выборке, составленной из доходов служащих финансовых компаний. Выборка должна давать правильное, неискажённое представление о генеральной совокупности, или, как говорят, должна быть репрезентативной. Для такой выборки представление о параметрах технологических процессов будет отражать реальное положение, если пропорции между вероятностями появления показателя качества продукции в выборке соответствуют пропорциям в генеральной совокупности. Если свойства генеральной совокупности заранее неизвестны, то за неимением лучшего следует использовать простой случайный выбор. Это означает, что все элементы генеральной совокупности должны иметь равные шансы попасть в выборку.

Абсолютные величины характеризуют размеры изучаемых явлений. Единицами их измерений являются следующие показатели:

• натуральные (гектары, центнеры, кормовые единицы,);

• условные,

• трудовые,

• стоимостные (рубли).

В свою очередь, они подразделяются на индивидуальные и суммарные показатели. При этом абсолютные статистические величины, выражающие размеры конкретной единицы совокупности, называют индивидуальными. К ним относятся, например, размер площади земель, закрепленных за хозяйствами в бессрочное пользование, урожайность сельскохозяйственных культур конкретного сельскохозяйственного предприятия и др. В процессе земельно-кадастровых работ часто возникает необходимости сравнить одни абсолютные величины с другими, показать отношение одной величины к другой. Для такого сравнения используют относительные величины, которые выражаются коэффициентами, показывающими, в сколько раз одна абсолютная величина больше или меньше другой, и процентами, когда частное от деления одной величины на другую умножается на 100. Для характеристики изменений земельно-кадастровых сведений во времени используются относительные величины динамики, которые выражают степень изменения данных за определенный период времени. Величины динамики, вычисленные к какому-либо периоду, называются базисными, а вычисленные к предыдущему периоду — цепными.

В практике земельно-оценочных работ кроме относительных величин применяют средние величины, которые выражают типичные размеры учитываемых явлений и дают обобщающую характеристику уровня по однородным признакам. Например, средние размеры контуров угодий, площади землепользования, урожайности сельскохозяйственных культур, валовой продукции сельскохозяйственного производства можно установить по индивидуальным значениям этих показателей в общей совокупности.

Различают несколько видов средних величин: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, мода и медиана. Средняя арифметическая простая применяется в тех случаях, когда отдельные величины признака встречаются один раз или одинаковое число раз. Она исчисляется по формуле в результате деления суммы индивидуальных значений на их количество:

= , (2.1)

где – средняя арифметическая величина признака; x₁ , x_{2 …}x_n – индивидуальные значения признаков; n – количество индивидуальных значений признаков.

Средней арифметической взвешенной пользуются в тех случаях, если от­дельные значения признаков имеют неодинаковое число повторений. Она определяется по формуле:

= , (2.2)

где f₁ , f₂ , … ,f_n — удельные веса индивидуальных значений признаков.

Средняя арифметическая взвешенная находит наибольшее применение при статистической обработке земельно-кадастровых данных, в частности, при выполнении работ по оценке земель.

Средняя гармоническая применяется в тех случаях, когда невозможно' использовать формулы средних арифметических величин. По сути, это ве­личина, обратная средней арифметической, и ее применяют, в частно­сти, когда веса приходится не умножать, а делить на варианты или умно­жать на обратные их значения.

Средняя гармоническая простая определяется по формуле:

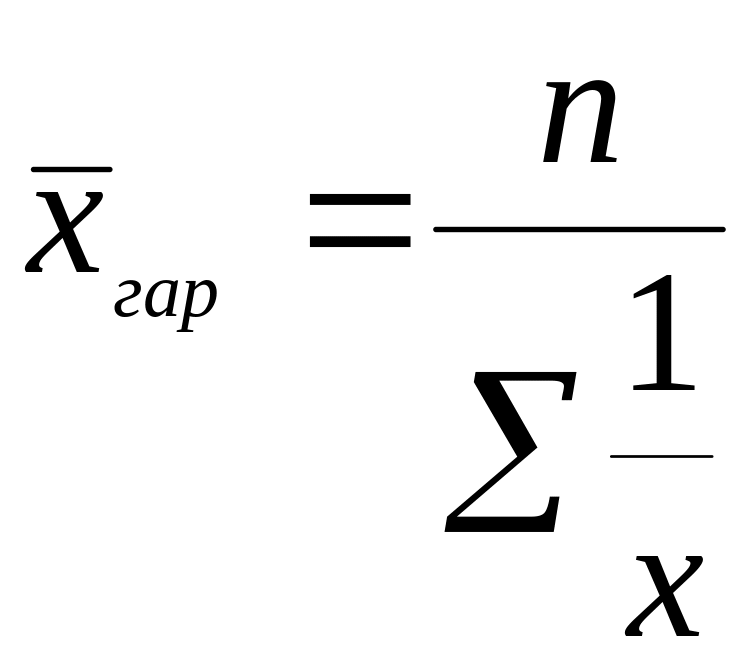. (2.3)

Если же веса отдельных вариантов неодинаковы, применяется формула средней гармонической взвешенной:

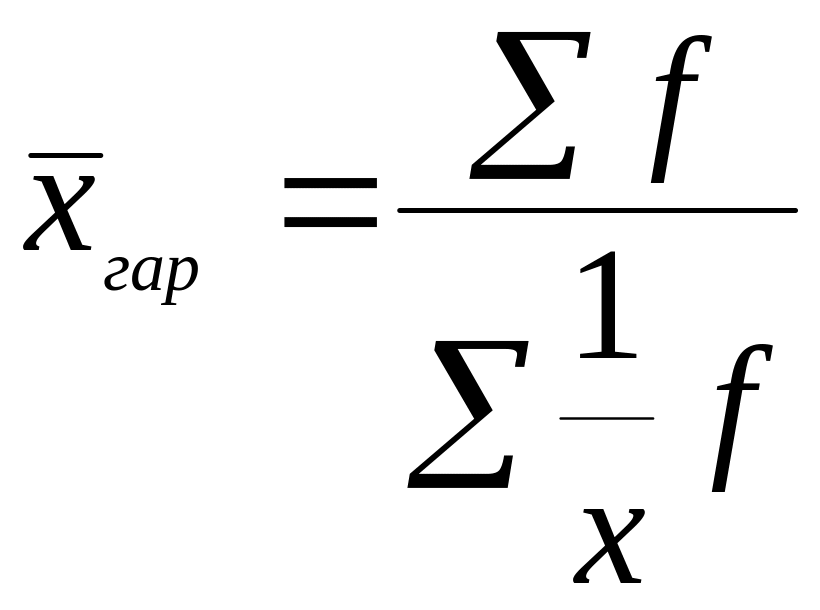. (2.4)

Для характеристики изучаемых признаков, кроме средних арифметических и средних гармонических величин, используются и такие средние величи­ны, как мода и медиана.

Модой называется величина признака, которая встречается в данной совокупности наиболее часто.

Медианой, или серединным вариантом, на­зывается значение варьирующего признака, который находится в середи­не ряда значений, расположенных в порядке возрастания или убывания. Для определения места медианы в вариационном ряду необходимо в сум­ме частот этого ряда прибавить единицу и полученный результат разделить на два.

Знание средних величин не решает всех задач при статистической обра­ботке земельно-кадастровых данных. Важно также располагать показателя­ми, которые характеризуют отклонение отдельных значений от средней величины. Для этого используются следующие показатели: размах вариа­ции, эмпирическая дисперсия.

Размах вариации (амплитуда колебаний) исчисляется как разность между крайними значениями варьируемого признака и дает представление лишь о крайних пределах вариации (максимальном и минимальном). Однако этот показатель не обеспечивает анализа степени изменчивости признака.

Другой показатель – эмпирическая дисперсия s – дает наиболее полную характеристику изменчивости признака и исчисляется по формуле:

, (2.5)

Эмпирической дисперсией называют среднюю арифметическую квадратов отклонения результатов наблюдений от средней арифметической.

Вариационный ряд – последовательность каких-либо чисел, расположенная в порядке возрастания их величин.

Интервальным вариационным рядом называют таблицу, позволяющую судить о распределении частот между интервалами варьирования значений признака.

Вариационные ряды (безинтервальный и интервальный) площадей объектов недвижимости города Кемерово приведены в таблицах 2.1 и 2.2.

Таблица 2.1 – Безинтервальный вариационный ряд площадей объектов недвижимости

Величина	Частота
42	1
44	6
45	1
46	1
48	2
49	1
50	4
51	3
52	1

Таблица 2.2 – Интервальный вариационный ряд площадей объектов недвижимости

Интервал	k
37-52	20
52-62	12
62-72	5
72-82	9
82-92	2
92-102	1
102-112	1

Полигон служит для изображения дискретного вариационного ряда. Полигон частот — один из способов графического представления плотности вероятности случайной величины. Представляет собой ломаную, соединяющую точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов.

Гистограмма служит для изображения интервального вариационного ряда.

Гистограмма — способ графического представления табличных данных. Количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны. Чаще всего для удобства восприятия ширину прямоугольников берут одинаковую, при этом их высота определяет соотношения отображаемого параметра. Таким образом, гистограмма представляет собой графическое изображение зависимости частоты попадания элементов выборки от соответствующего интервала группировки.

Поверка нулевой гипотезы. Нулевая гипотеза — гипотеза, которая проверяется на согласованность с имеющимися выборочными (эмпирическими) данными. Часто в качестве нулевой гипотезы выступают гипотезы об отсутствии взаимосвязи или корреляции между исследуемыми переменными, об отсутствии различий (однородности) в распределениях (параметрах распределений) двух и/или более выборках. В стандартном научном подходе проверки гипотез исследователь пытается показать несостоятельность нулевой гипотезы, несогласованность её с имеющимися опытными данными, то есть отвергнуть гипотезу. При этом подразумевается, что должна быть принята другая, альтернативная (конкурирующая), исключающая нулевую, гипотеза.

Коэффициент корреляции (или парный коэффициент корреляции) в теории вероятностей и статистике — это показатель характера взаимного стохастического влияния изменения двух случайных величин. Коэффициент корреляции обозначается латинской буквой R в математической статистике (r в статистике) и может принимать значения от −1 до +1. Если значение по модулю находится ближе к 1, то это означает наличие сильной связи, а если ближе к 0 — связь слабая или вообще отсутствует.

При коэффициенте корреляции равном по модулю единице говорят о функциональной связи, то есть изменения двух величин можно описать математической функцией.

Уравнение линейной регрессии имеет вид:

y=b₀+b₁x, (2.6)

где y: y₁, y₂, y₃… y_n; x: x₁, x₂, x₃… x_n;

.

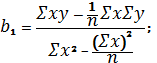
Контрольные вопросы

1. Типы статистических данных.

2. Оценка генеральной совокупности по выборке.

3. Полигон

4. Гистограмма.

5. Мода.

6. Медиана

7. Размах.

8. Вариационный ряд.

9. Поверка нулевой гипотезы.

10. Коэффициент корреляции