-
Задача 2
Дана матрица ковариаций и ожидаемые доходности для 6 инвестиционных проектов. Сформировать оптимальный портфель при условии, что инвестиционный капитала равен 100 тыс. руб. и значение неустойки равно 0,1.
Таблица 2 – Значения оптимальной доходности
|
|
Проект 1 |
Проект 2 |
Проект 3 |
Проект 4 |
Проект 5 |
Проект 6 |
|
Ожидаемая доходность, % |
0,11 |
0,02 |
0,25 |
0,12 |
0,14 |
0,48 |
Таблица 3 – Матрица ковариаций
|
0.0289 |
0.0357 |
0.0748 |
0.0425 |
0.0527 |
0.0323 |
|
0.0357 |
0.0441 |
0.0924 |
0.0525 |
0.0651 |
0.0399 |
|
0.0748 |
0.0924 |
0.1936 |
0.1100 |
0.1364 |
0.0836 |
|
0.0425 |
0.0525 |
0.1100 |
0.0625 |
0.0775 |
0.0475 |
|
0.0527 |
0.0651 |
0.1364 |
0.0775 |
0.0961 |
0.0589 |
|
0.0323 |
0.0399 |
0.0836 |
0.0475 |
0.0589 |
0.0361 |
Код программы:
// Список инвестиционных возможностей
Investments = { Invest0, Invest1, Invest2, Invest3, Invest4, Invest5 };
// Инвестиционные данные
Return = [ 0.11, 0.02, 0.25, 0.12, 0.14, 0.48 ]; // Ожидаемая прибыль
Covariance = [
[ 0.0289, 0.0357, 0.0748, 0.0425, 0.0527, 0.0323 ],
[ 0.0357, 0.0441, 0.0924, 0.0525, 0.0651, 0.0399 ],
[ 0.0748, 0.0924, 0.1936, 0.1100, 0.1364, 0.0836 ],
[ 0.0425, 0.0525, 0.1100, 0.0625, 0.0775, 0.0475 ],
[ 0.0527, 0.0651, 0.1364, 0.0775, 0.0961, 0.0589 ],
[ 0.0323, 0.0399, 0.0836, 0.0475, 0.0589, 0.0361 ]
]; // Матрица ковариаций
Wealth = 100; // Начальный капитал
Rho = 0.1; // Неустойка (увеличивается от 0.001 до 1.0).
Полученное решение:
Интерпретация:
Для того чтобы портфель был оптимальным, следует сделать инвестиции только в проект №6, тогда максимальная прибыль составит 30 тыс. руб.
-
Задача3
Найти оптимальный портфель максимальной эффективности для 10 активов, при начальном капитале равном 100 и неустойке 0,01.Значения ожидаемой доходности и среднеквадратического отклонения в % представлены в таблице 2:
Таблица 4 - Список инвестиционных возможностей
|
Актив |
Ожидаемая доходность, % |
Среднеквадратическое отклонение, % |
|
Актив №1 |
0,41 |
0,05 |
|
Актив №2 |
0,32 |
0,09 |
|
Актив №3 |
0,45 |
0,11 |
|
Актив №4 |
0,12 |
0,21 |
|
Актив №5 |
0,24 |
0,18 |
|
Актив №6 |
0,18 |
0,10 |
|
Актив №7 |
0,29 |
0,19 |
|
Актив №8 |
0,09 |
0,03 |
|
Актив №9 |
0,15 |
0,25 |
|
Актив №10 |
0,22 |
0,40 |
Для решения данной задачи построим матрицу ковариаций:
Таблица 5 – Матрица ковариаций
|
0.0025 |
0,0045 |
0.0055 |
0.0105 |
0.0090 |
0.0050 |
0.0095 |
0.0015 |
0.0125 |
0.0200 |
|
0.0045 |
0.0081 |
0.0099 |
0.0189 |
0.0162 |
0.009 |
0.0171 |
0.0027 |
0.0225 |
0.0360 |
|
0.0055 |
0.0099 |
0.0121 |
0.0231 |
0.0198 |
0.0110 |
0.0209 |
0.0033 |
0.0275 |
0.0440 |
|
0.0105 |
0.0189 |
0.0231 |
0.0441 |
0.0378 |
0.0210 |
0.0399 |
0.0063 |
0.0525 |
0.0840 |
|
0.0090 |
0.0162 |
0.0198 |
0.0378 |
0.0324 |
0.0180 |
0.0342 |
0.0054 |
0.0450 |
0.0720 |
|
0.0050 |
0.009 |
0.0110 |
0.0210 |
0.0180 |
0.01 |
0.0190 |
0.0030 |
0.0250 |
0.0400 |
|
0.0095 |
0.0171 |
0.0209 |
0.0399 |
0.0342 |
0.0190 |
0.0361 |
0.0057 |
0.0475 |
0.0475 |
|
0.0015 |
0.0027 |
0.0033 |
0.0063 |
0.0054 |
0.0030 |
0.0057 |
0.0009 |
0.0075 |
0.0120 |
|
0.0125 |
0.0225 |
0.0275 |
0.0525 |
0.0450 |
0.0250 |
0.0475 |
0.0075 |
0.0625 |
0.1000 |
|
0.0200 |
0.0360 |
0.0440 |
0.0840 |
0.0720 |
0.0400 |
0.0760 |
0.0120 |
0.1000 |
0.16 |
Полученное решение:
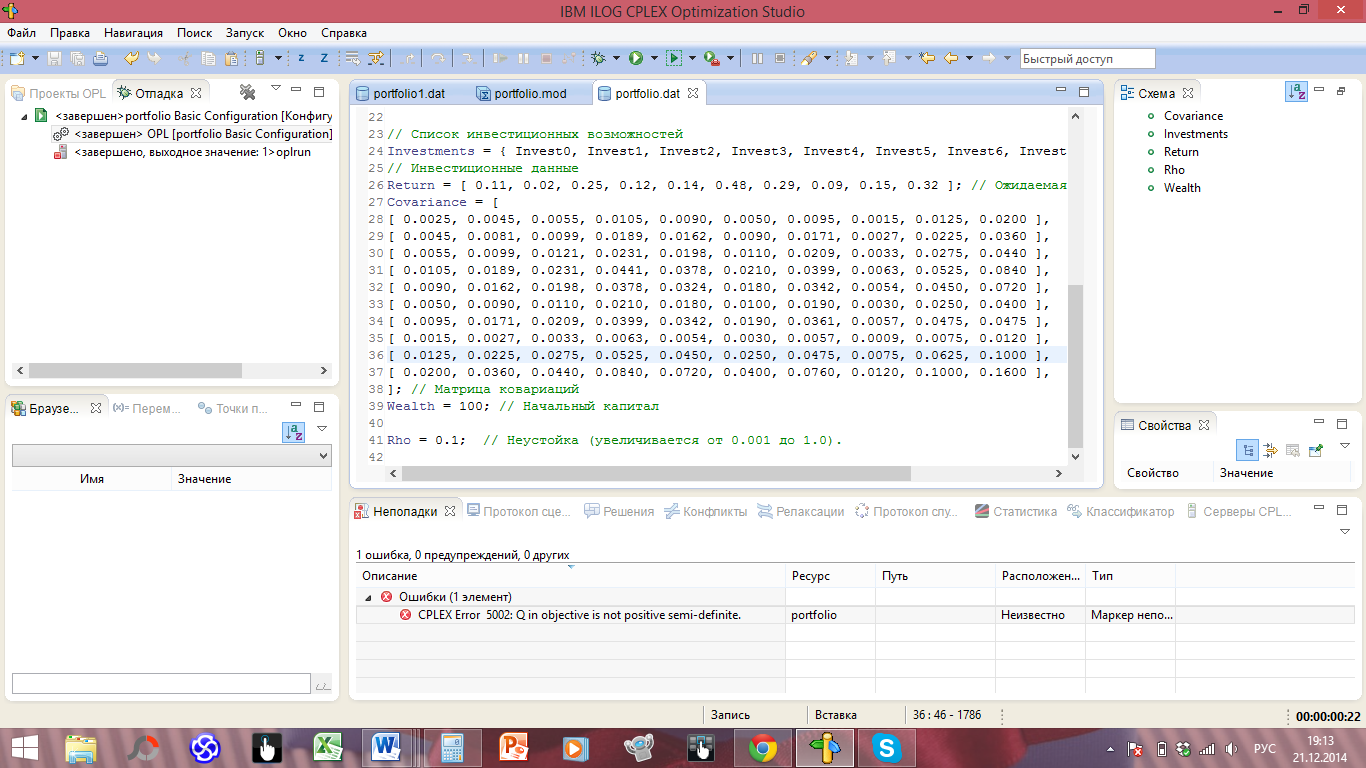
Интерпретация: исходные данные не могут использоваться для формирования оптимального портфеля, т.к. значение целевой функции не принимает положительного значения, следовательно, инвестору стоит воздержаться от вложения средств.