Добавил:

Teana Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Таврический Национальный Университет им. В.И. Вернадского

Предмет:

Экономика

Файл:

Неманипулируемые механизмы обмена в активных системах - Коргин Н.А

..pdf

Скачиваний:

Добавлен:

24.05.2014

Размер:

1.06 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 136 7 8 9 10 11 12 13 > Следующая >>>

Это полностью соответствует постановке задачи построения механизма ОУ для ОС, введенной в предыдущей главе.

Для решения поставленной задачи необходимо уточнить вид функции полезности от обмена для АЭ. Для этого введем следующие предположение относительно функции c(y,r):

А.4. r Ω, х2 Х

1) c(х2,r) непрерывна по r;

2) dc(x2 ,r) < 0; dr

3)d 2c(x2 ,r) < 0; dx2 dr

4)c(х2,r) удовлетворяет А.1.

Содержательно, данное условие прежде всего показывает, что, чем больше значение типа АЭ, тем меньше его затраты на выполнение одного и того же действия.

Лемма 2. Условие А.4. обеспечивает выполнение условия F1 и F2 для функции прибыли от обмена АЭ f1 (x1 , x2 ,r).

Доказательство. Т.к f1 (x1 , x2 ,r) = х1 - c(х2,r), то, с учетом А.4.

r Ω, х Х	∂f1 (x1 , x2 ,r)				= −	dc(x2 ,r)	> 0 ,
		∂r				dr

т.е. выполнено F1. Также, из А.4. следует
r Ω, х Х	∂f (x , x ,r)				= −	d 2c(x ,r)		> 0 ,
	1	∂x2	∂r			dx2 dr
		1		2		2

что соответствует F2a. Также очевидно,

r Ω, х Х ∂f1 (x1 , x2 ,r) = 0 ,

∂x1∂r

что соответствует F2b.■

Следовательно, для построения механизма ОУ для данной обменной

схемы можно использовать общий метод построения неманипулируемых механизмов обмена, полученные в главе 1.

2.2. Построение эффективных и неманипулируемых механизмов обмена для двухэлементных иерархических обменных схем

Дискретный подход. Рассмотрим случай, когда параметр r (тип АЭ) может принимать только два “граничных” значения, т.е. АЭ может быть двух типов - с функцией затрат c(y,r0) или с c(y,r1), где r0 = rmin, r1 = rmax.

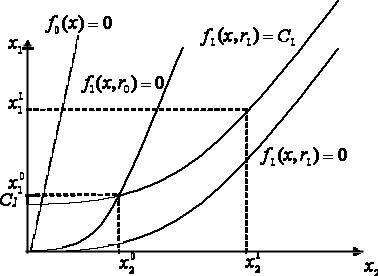
Рисунок 7 иллюстрирует “графический” метод построения неманипулируемого механизма обмена. На рисунке изображен

преобразованный ящика Эджворта в координатах	трансфертов. Линия
f0 (x) = 0 задает ограничения ИР для центра,	линии f1 (x,r0 ) = 0 и

f1 (x, r1 ) = 0 для АЭ соответствующих типов. Для каждого из возможных типов АЭ выбирается точка на множестве Х - ri → xi = (x1i , x2i ) .

Рис. 7. «Графический» метод

Точка для наихудшего типа АЭ (в нашем случае наименьшего) выбирается на кривой f1 (x, r0 ) = 0, точка для наилучшего типа АЭ выбирается на кривой f1 (x, r1 ) = C1 , так чтобы f1 (x0 , r1 ) = C1 . Учитывая вид функции полезности АЭ, получим

(23)x10 = c(x20,r0);

(24)x11 = c(x21,r1) + C1;

(25)С1= c(x20,r0) – c(x20,r1).

Значения величин x20 и x21 определяются из решения задачи нелинейного программирования:

(26) x2i = arg max K(x1(x2),x2,ri), 0≤ x2i ≤ Y2, 0≤ x1i ≤ Y1, i=0,1,

где K(·) – критерий эффективности, т.е. действие АЭ x2i должно быть оптимальным (с точки зрения центра) при условии, что в обмене участвует АЭ типа ri. На критерий эффективности необходимо наложить следующие требования:

А.5 В детерминированной ОС, соответствующей рассматриваемой ОС с неопределенностью, решение задачи обмена с критерием K(·) эквивалентно решению детерминированной задачи, т.е. при r0 = r1 (26) и (20) дают одинаковое значение x2.

Данное требование всего лишь обеспечивает возможность анализа задач с неопределенностью путем экстраполяции их к детерминированным задачам. Например, если целью центра является максимизация ожидаемой прибыли от обмена (критерием эффективности является ожидаемая полезность центра Ef0), и он имеет некоторую информацию о вероятностном распределении типов АЭ - pi, i = 0,1, p0 + p1 = 1, то можно записать:

x2i = arg max {(H(x20 ) – c(x20,r0)) p0 + (H(x21) – c(x21,r1) – C1) p1}, i = 0,1.

Собственно сам механизм таков – АЭ сообщает центру оценку s=ri своего типа, центр назначает АЭ обмен xi = (x1i , x2i )

Для предложенного «графического» метода справедлива следующая лемма.

Лемма 3. Для сообщения АЭ истинной оценки своего типа необходимы следующие ограничения:

(27) xj 0 ≤ xj1 , j =1,2.

Доказательство. Принцип построения механизма, который выражен в (23) - (25) требует, что бы

f	(x	0 , x	0 ,r ) = 0 ;
1	1	2	0
f	(x	0 , x	0 ,r ) = f		(x 1	, x	1 ,r ) = C .
1	1	2	1	1	1	2	1	1

	Из (23) - (25) также следует
f	(x 1	, x 1	,r ) = [c(x			1 ,r ) - c(x 1 ,r )] - [c(x						0 ,r ) - c(x		0	,r )]
1	1	2	0		2	1	2		0		2	1		2	0
	Из условия А.4 (точнее, его трактовки в дискретном случае) следует,
что c(x 1			,r ) - c(x 0			,r ) ³ c(x 1		,r ) - c(x 0 ,r ) при x						0 £ x 1 .
		2	0		2	0	2		1		2	1	2		2
	Также, из (23) - (25) и А.4 получаем, что x 0													= x 1		при x 0	= x	1 ,	x 0	> x 1
													1		1	2		2	1	1
при x 0 > x 1 ,				x 0	< x 1		при x 0	< x 1 .
		2	2	1		1	2		2
	Получается,					что		f	(x 1	, x 1	,r ) £ 0		при			x 0 £ x 1 , j =1,2,				и
								1	1	2	0					j	j
f	(x 1	, x 1	,r ) > 0		при		x 0 > x	1 , j =1,2			соответственно.					С учетом гипотезы
1	1	2	0				j	j

благожелательности получаем, что при выполнении (27) АЭ будет сообщать истинную оценку своего типа ri.■

Из (23) - (25) видно, что, если x20 = x21, то x10 = x11. Т.е. для АЭ разных типов назначается одинаковый план. Данная ситуация не противоречит принципу открытого управления, так как, с учетом гипотезы благожелательности, АЭ будет сообщать свой истинный тип, что следует из леммы 3.

Итак, (23) - (25) с учетом требования (27) дают решение поставленной нами задачи при условии, что возможны только два типа АЭ. При

увеличении количества возможных значений типов АЭ принцип построения механизма обмена не меняется. Запишем множество возможных типов АЭ: Ω = (r0,r1,…,rn), r0 = rmin, rn = rmax. Тогда для пары

xi = (x i , x i		) , i =		по аналогии с (23) - (26) можно выписать следующие
xi = (x i , x i		) , i =	0,n	по аналогии с (23) - (26) можно выписать следующие
1	2
условия:
(28) x1i	= c(x2i,ri) + Ci, i =					;
(28) x1i	= c(x2i,ri) + Ci, i =				0,n	;
(29) Сi=åi		(c(x2 j−1,rj-1 ) - c(x2 j−1,rj )), C0=0, i =						;
(29) Сi=åi		(c(x2 j−1,rj-1 ) - c(x2 j−1,rj )), C0=0, i =					0,n	;
	j=1

(30) x2i = arg max K(x2,ri), 0≤ x2i ≤ Y2, 0≤ x1i ≤ Y1, i = 0,n .

При сообщении АЭ заявки s = ri центр назначает ему план обмена xi = (x1i , x2i ) . Также сохраняется требования (27):

(27а)"i =1,n, xj i−1 £ xj i , j =1,2 .

Также, очевидно, что если совпадение одной из компонентов плана для разных типов АЭ означают, что планы для данных типов АЭ эквивалентны (можно сказать, что с точки зрения центра данные типы АЭ эквивалентны)

Теорема 2. Если выполнена гипотеза благожелательности, то

доминантной стратегией АЭ в предложенном механизме обмена будет

сообщение истинной оценки своего типа. Т.е. s = r*.
Доказательство. Запишем прибыль АЭ типа i (r* = r	) -	f	(x , x	,r )
i		1	1 2	i

при выполнении им плана, предлагаемого для типа j (s = rj), используя (28)

и (29):

(31)

j , x

j ,r ) = c(x

) + C

- c(x

i ,r ) .

Из (31) получаем, что f1(x1i,x2i, ri) = Ci. Также из (31) и (29) следует, что

(x i−1

, x

i−1 ,r ) = c(x

i−1 ,r

) + C

- c(x i ,r )

Þ f1(x1i-1,x2i-1, ri)= Ci. Для случая j

i−1

= i + 1 (31) с учетом (29) (выразив Ci+1 через Ci) можно записать:

(32)

(x i+1

, x i+1 ,r ) = C

+ c(x

i+1 ,r

) - c(x i

) + c(x

i ,r ) - c(x i+1 ,r ).

i+1

Из условия А.4, с учетом (27а), очевидно, что

c(x

i+1 ,r ) - c(x

i ,r ) ³ c(x i+1

) - c(x i ,r

i+1

Следовательно,

(x i+1 , x

i+1 ,r ) £ f

(x i , x i

,r ) .

Аналогично, можно показать, что " j =

i +1,n

(x j , x

,r ) £ f

(x i , x

,r ) .

Для случая j = i - 2

(31) с учетом (29) (выразив Ci-2

через Ci) можно

записать:

(33)

(x i−2 , x i−2

,r ) = C

+ c(x i−2 ,r

) - c(x i−2 ,r ) + c(x

i−1 ,r ) - c(x

i−1 ,r

) .

i−1

Из условия А.4, с учетом (27а), очевидно, что

c(x

i−1 ,r

) - c(x

i−2 ,r

) ³ c(x i−1

,r ) - c(x i−2

,r ) .

i−1

Следовательно,

(x i−2 , x

i−2 ,r ) £ f

(x i

, x i

,r ) .

По аналогии с (П.4) можно показать, что " j = 0,i - 2

f1 (x1 j , x2 j ,ri ) ≤ f1 (x1i , x2i ,ri ) .

Из приведенных выше рассуждений следует, что АЭ типа ri получает максимальную прибыль от обмена при сообщениях s = ri и s = ri-1. Учитывая гипотезу благожелательности, получаем, что АЭ типа ri сообщит s = ri, потому что из двух эквивалентных планов он выберет лучший для центра, т.е. (x1i, x2i).■

Т.е. построенный механизм обмена π (s) = (x1 (s), x2 (s)) , определяемый (28) - (30), является механизмом открытого управления. Учитывая, что

для двухэлементных задач поиск механизмов планирования можно ограничить классом механизмов ОУ [52], получаем, что дискретный метод позволяет найти механизм обмена максимальной эффективности.

Задача 1. Построить эффективный и неманипулируемый механизм обмена для ОС, рассмотренной в разделе 2.1. Функция полезности центра

x 2

от обмена f0 (x1 , x2 ) = x2 − x1 . Функция полезности АЭ - f1 (x1 , x2 ) = x1 − 22r .

Критерий эффективности центра - максимизация ожидаемой полезности

от обмена Ef0 (π (s)) → max . Множество возможных значений типа АЭ –

π ( s)

n+1 точек на отрезке [rmin,rmax], r0 = rmin>0, rn = rmax.

Функция затрат АЭ имеет следующий вид

c(x,r) = x2 . 2r

Данная функция удовлетворяет требованиям А.4. r Ω, х > 0

непрерывна по r и по х;

dc(x ,r)

= −

< 0;

2r2

d 2c(x,r)

= −

< 0;

dxdr

dc(x ,r)

> 0;

d 2c(x ,r)

= r−1 > 0 .

dx2

Следовательно, можно построить механизм ОУ π (i) = (x1i , x2i ) . Из (28) и (29) получаем.

i−1	x	j 2		1		1
i−1	x			1		1
Сi=å	2		(		-		) , i=1, n , C0=0;
Сi=å	2		(	rj	-	rj+1	) , i=1, n , C0=0;
j=0	2			rj		rj+1

x1i = x2i 2 + Ci, i = 0, n . 2ri

Механизм должен максимизировать ожидаемую прибыль центра при

ограничениях 0≤ x2i ≤ Y2, 0≤ x1i ≤ Y1, i =

Т.е. необходимо решить

0, n

задачу нелинейного программирования:

∂L

(x2 ,

) £ 0;

∂L

(x2 ,

) ³ 0;

∂L

(x2 ,

)x2 = 0;

∂

(x2 ,

)

= 0;

¶x2

¶λ

¶x2

¶λ

³ 0,

³ 0 .

Здесь

x2 = (x2

0 ,..., x2 n ) ,

= (λ0 ,...,λ2n+1 ),

L = Ef0 + å[λ2i (Y2

- x2i ) + λ2i+1 (Y1

- x1i )].

i=0

Учитывая, что

Ef0 (W) = å pi (x2i -x1i ) = å

ê pi x2i

i 2

+ ( 1 - 1

) å p j

n 2

- x2 ( pi

)ú + pn (x2 n - x2 )

n−1

2 ri

ri+1 j=i+1

2rn

i=0

i=0 ê

получим:

~ i

~ n

(34) x2

= min(

, x2

,Y2 ) , i=0, n -1, x2

= min(rn , x2

,Y2 );

å p j

j=i

ri+1 j=i+1

i−1

j 2 ù1/ 2

= ê2riY1 - å(

)x2

ú , i=0, n ;

rj+1

j=0

x i 2

i−1

j 2

0 2

(35) x1

+ å

(

) , i=1, n , x1

2ri

j=0

rj+1

2r0

~ i

Точки

i=0, n

значение трансферта типа 2 при выходе на

ограничение x1i ≤ Y1.

Очевидно, что если для некого типа АЭ rl данное

		l	~ l		j
				), то для всех j=l + 1, n		=
ограничение вступает в силу (x2			= x2		x2
~ j	~ l	.Т.е. планы для всех типов АЭ, начиная j и лучше, совпадают. При
x2	= x2

этом планы для типов АЭ, хуже j остаются неизменными.

Если распределение типа АЭ взять равномерным - pi = n 1+1 , то (34)

можно переписать следующим образом:

- i

n - i

−1

~ n

~ i

ç n +1

= min(ç

, x2

,Y2 ) , i=0, n -1,

= min(rn , x2

,Y2 ).●

ri+1

Задача 2. Построить эффективный и неманипулируемый механизм обмена для ОС с линейными функциями полезности Ц и АЭ:

(36)f0 (x1 , x2 ) = x2 − cx1 ;

(37)f1 (x1 , x2 ) = rx1 − x2 .

Данный вид функций полезности используется чаще всего при описании процессов обмена между крупными промышленными предприятиями. Задача центра – максимизация гарантированной

относительной прибыли от обмена min	f0 (π (s))	® max . Множество
	max f0 det (s)
s		π

возможных значений типа АЭ – n+1 точек на отрезке [rmin,rmax], r0 = rmin>0,

rn = rmax.

Распределение ресурса в схеме такое же, как в рассмотренном выше примере - весь ресурс первого типа Y1 сосредоточен у центра, весь ресурс второго типа Y 2 – у АЭ. Причем существенным будем считать ограничение на ресурс первого типа.

Механизм имеет следующий вид: x i = μ nY (ri - c(1-

)) ,

x i =

μ n

Y ,

μi

μi = (1 + r

- r

1 )−1 , i=0, n .●

j=1

- c

Получив механизм ОУ для задачи обмена в схеме из двух участников с внутренней неопределенностью в случае дискретного распределения

возможных типов АЭ, перейдем к рассмотрению непрерывного случая распределения.

Непрерывный подход к построению эффективного и неманипулируемого механизма обмена для «базовых» ОС основан на методе, изложенном в разделе 1.5.

В непрерывном случае область возможного значения типа АЭ будет

задаваться как отрезок - Ω =

[rmin,rmax]. Получаем, что механизм ОУ

π (s) = (x1 (s), x2 (s)) должен удовлетворять следующим требованиям:

dx1

(r) -

∂c

(x2

(r),r)

dx2

(r) = 0;

¶x2

∂c

(r),r)

dx2

(r) £ 0.

¶x2¶r

Обе компоненты плана являются неубывающими функциями своего

аргумента

ÎW ,

dx1

(s ) ³ 0,

dx2

(s ) ³ 0 .

Так как наихудшим из возможных типов АЭ является тип rmin, то, с

учетом условий ИР ν1 (rmin ) = 0.

Выражение (9) для рассматриваемого

случая запишется следующим образом:

(38)ν1 (r) =

¶c

(x2 (τ ),τ )dτ .

rminò

¶r

Учитывая, что

ν1 (r ) = x1 (r) − c(x2 (r),r) ,

можно сделать замену переменных

r¶c

(39)x1 (r) = c(x2 (r),r) - rminò ¶r (x2 (τ ),τ )dτ ,

которая позволяет свести задачу построения механизма ОУ к решению следующей задачи.

(40) x2(r) = arg max K(x1,x2,r), 0≤ x2(r)≤ Y2, 0≤ x1(r) ≤ Y1.

Произведем проверку эквивалентности дискретного и непрерывного решений рассматриваемой задачи. Переменная n отражает мелкость разбиения множества Ω = [rmin,rmax]:

= r

r = r

+ i

= rmax − rmin .

, i =1...n

min

Справедлива следующая лемма

Лемма 4. ν (ri

) = limCi , где Ci определяется из (29), ν (ri ) - из (38).

n→∞

Доказательство.

Выражение (29)

можно

переписать следующим

образом:

Сi=åi−1 (c(x2 j−1,rj-1 ) - c(x2 j−1,rj−1

+ )), C0=0, i =

0...n

j=0

Очевидно, что

lim(c(x

j−1,r

j-1

) - c(x j−1

j−1

))= − ∂c (x

j−1 ,r

j−1

)dr .

→0

∂r

Учитывая, что x

соответствует

r , т.е x i = x

(r ), получаем, что

limCi

= limCi

= òr

− ∂c

(x2 (τ ),τ )dτ .■

n→∞

→0

rmin

∂r

Как следствие леммы 4, получаем, что при n → ∞ , выражения (28) и (39) эквивалентны. Т.е. решение задачи в дискретном случае соответствует решению задачи в непрерывном случае. Проиллюстрируем полученное решение на примере.

Задача 3. Построить эффективный и неманипулируемый механизм обмена для ОС, рассмотренной в разделе 2.1. Функция полезности центра

x 2

от обмена f0 (x1 , x2 ) = x2 − x1 . Функция полезности АЭ - f1 (x1 , x2 ) = x1 − 22r .

Критерий эффективности центра Ef0 (π (s)) → max . Множество

π ( s)

возможных значений типа АЭ –отрезок [rmin,rmax], rmin>0.

Функция затрат АЭ имеет следующий вид

c(x,r) = x2 . 2r

<<< < Предыдущая 1 2 3 4 56 / 136 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете Экономика

#
24.05.2014902.44 Кб19Налог с продаж - А.А. Кузнецова.rtf
#
24.05.201415.2 Mб396Настольная Книга Управляющего Складом - Джеймс Томпкинс.doc
#
24.05.201411.53 Mб120Национальная экономика - Шульга В.А..pdf
#
24.05.2014201.9 Кб31Недобросовестная рыночная практика на финансовых рынках - Азимова Л..pdf
#
24.05.2014110.66 Кб18Некоторые аспекты банковского обслуживания ФПГ - Минина Т. И..pdf
#
24.05.20141.06 Mб19Неманипулируемые механизмы обмена в активных системах - Коргин Н.А..pdf
#
24.05.201499.22 Кб32Непрерывный контроль процесса достижеия цели - Гайдай А.А., Руссман И.Б..pdf
#
24.05.20141.61 Mб20Неформальный сектор экономическое поведение детей и взрослых. - Борисова Л.Г., Солодова Г.С., Фадеева О.П., Харченко И.И.pdf
#
24.05.20141.9 Mб41Нечетко- множественный анализ риска фондовых инвестиций - Недосекин А.О..pdf
#
24.05.20141.9 Mб22Нечетко-множественный анализ риска фондовых инвестиций - Недосекин А. О..pdf
#
24.05.20141.06 Mб27Неэмиссионные ценные бумаги - Макеев А. В..pdf