Оптимальные иерархические структуры - Воронин А.А., Мишин С.П

той или иной операции. Однако в общем случае для нормального функционирования системы этого недостаточно, так как технологические связи между операциями (исполнителями) специально не контролируются. То есть необходимо создание управляющих центров, которые координируют взаимодействие элементов.

Рис. 2.1. Технологический граф процесса подписания договоров.

Считаем технологический граф связным1, так как в

противном случае происходит декомпозиция на никак не связанные друг с другом части, которые могут быть рассмотрены по отдельности. Для того чтобы каждая связь кем-то контролировалась, и каждая вершина была подчинена только одному “начальнику”, необходимо наличие управляющего центра,

всевозможных деревьев организации: Ω = D( f ) .

1 Имеется в виду связность при рассмотрении ребер как неориентированных. В этом случае при любом разбиении множества вершин N на части N1 и N2 ,

N = N1 È N2 , N1 Ç N2 = Æ существуют ребра, идущие из N1 в N2 или наоборот.

61

Рассмотрим группу элементов g 2N \ { }. Через lT (g) обозначим суммарную интенсивность потоков внутри группы, то

соответствующий группе g , координирует потоки между подгруппами g1,K, gk . Их суммарная интенсивность, очевидно, равна lT (g) − lT (g1 ) −K− lT (gk ). Предполагаем, что затраты на

содержание (функционирование) управляющего центра являются некоторой неотрицательной функцией K(×) от интенсивности координируемого потока. Тогда можно записать функционал стоимости организации взаимодействия подгрупп g1,K, gk

следующим образом:

PT ,K (g1,K, gk ) = K (lT (g1 K gk ) − lT (g1 ) −K− lT (gk )) .

Стоимость P(D) = åg V \ND P(g1,K, gk ) (QD (g) = {g1,K, gk }) содержания (функционирования) всей организации D будет

структурным функционалом и задача об оптимальной организации технологического взаимодействия – частный случай общей задачи об оптимальной организации на D( f ).

Построенные в главе III алгоритмы поиска оптимального

дерева могут быть использованы для решения задачи в общем случае. Кроме того, ниже доказываются некоторые аналитические результаты.

Частный случай поставленной задачи рассмотрен, например, в [37]. Связи между элементами (ребра технологического графа) характеризуются тремя градациями “интенсивности” взаимодействия: низкая, средняя и высокая, после чего

применяется эвристический алгоритм группировки наиболее “связанных” элементов, затем наиболее “связанных” групп и т.д.

На рис. 2.2 приведены примеры “надстройки” дерева организации над технологическим графом. На рисунке слева организация состоит из элементов технологического графа 1-7 и трех управляющих центров (узлов) I, II, III. Подчиненными узла I являются все маркетологи (элементы 1-3 технологического графа), подчиненными узла II – менеджеры и юрист (элементы 4-6), в подчинении узла III – узлы I, II и бухгалтер (элемент 7). Группы,

62

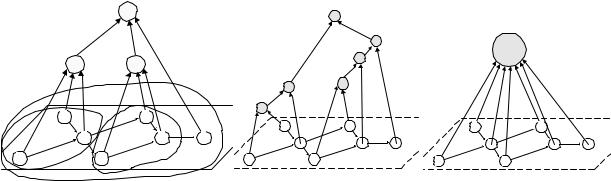
подчиненные узлам I, II, III, обведены криволинейными фигурами. В середине рисунка приведен пример 2-дерева, справа изображена веерная организация.

Рис. 2.2. Примеры структур системы управления технологическими связями.

вогнутый.

Доказательство. Пусть {g1,K, gk } – произвольный набор

непересекающихся групп, k ³ 3. Рассмотрим произвольное разбиение на поднаборы {h1,K, hi }, {hi+1,K, hk }, 1 < i < k (см. опр. 1.30). Рассмотрим следующие векторы l = lT (g) − lT (g1 ) −K − lT (gk ), l′ = lT (h) − lT (h1 ) −K − lT (hi ) , l′′ = lT (g) − lT (h) − lT (hi+1) − K− lT (hk ) ,

(выполнено первое неравенство утв. 2.1), то существует 2-дерево организации, оптимальное на D( f ) (см. следствие 1 к теор. 1.5). Если функция затрат субаддитивна (выполнено второе

63

неравенство утв. 2.1), то оптимальна веерная организация (см. следствие к теор. 1.6). В первом случае для решения задачи можно воспользоваться алгоритмами поиска оптимального 2-дерева, которые имеют меньшую сложность, чем для произвольного дерева (см. гл. III). Во втором случае оптимальная организация найдена.

ребрах технологического графа соответствующими величинами и рассмотреть вместо функции K(×) одномерную функцию затрат

K ¢(×).

Лемма 2.1. Если K(0) = 0 и одномерная функция затрат K(×)

неравенства изменятся на противоположные. Лемма доказана.

То есть при условиях леммы 2.1 выпуклость влечет супераддитивность, вогнутость – субаддитивность. Рис. 2.3 иллюстрирует полученные результаты. При вогнутой функции затрат (рис. 2.3 справа) выгоднее координировать один большой поток, чем несколько малых. То есть оптимальное дерево – веерная организация – содержит один центр, которому подчинены все элементы. При выпуклой функции затрат (рис. 2.3 слева) выгоднее координировать несколько малых потоков, чем один большой. То есть если некоторый центр координирует более двух групп, то выгоднее ввести еще один промежуточный центр. В результате оптимально 2-дерево организации, которое имеет максимальное количество центров управления.

64

причине в теории кодирования рассматриваются, в основном, префиксные коды, которые имеют наиболее простую процедуру декодирования.

называется оптимальным (кодом с минимальной избыточностью [48]), если величина p1ll +K+ pnln минимальна, то есть

минимальна средняя длина кодовых сообщений. Задача об

оптимальном коде состоит в поиске оптимального префиксного кода для заданных вероятностей.

k ≤ r . Сопоставим каждому из ребер (g1, g) ,…,(gk , g) символ

(букву) выходного алфавита, причем разным ребрам сопоставим разные символы. Полученное r -дерево будем называть помеченным (такие деревья описаны, например, в работе [42]).

Для сведения задачи об оптимальном префиксном коде к задаче об оптимальной организации докажем следующее утверждение о соответствии деревьев кодам.

Утверждение 2.2. Существует изоморфизм, при котором

каждому префиксному коду соответствует одно и только одно помеченное r -дерево D Dr ( f ), причем длина li кодового слова

wi равна длине пути из {ai } в f = {a1,K, an} в соответствующем

дереве.

Доказательство. Пусть задан некоторый префиксный код. Построим соответствующее ему r -дерево D Dr ( f ). В корне

r -дерева находится группа из всех символов входного алфавита, а в листьях – группы из одиночных символов. В каждую вершину r -дерева входит не более r ребер (r – число символов выходного алфавита). На первом шаге построения считаем, что дерево D состоит из одной изолированной вершины f . Построим

множества g1,K, gr следующим образом. В группу gi включим те

66

символы a j из f , для которых первая буква кодового слова wj равна bi . То есть в первое множество включаем символы, кодовые

слова которых начинаются с первой буквы выходного алфавита, во вторую – со второй, и так далее. Некоторые множества из g1,K, gr могут быть пустыми (если нет слов, начинающихся на данную букву). Добавим в r -дерево D непустые группы gi и ребра

(gi , f ), поставив в соответствие ребру (gi , f ) букву bi . В силу равенств f = g1 ÈKÈ gr и gi Ç g j = Æ получим, что f в D организуется из непересекающихся подгрупп QD ( f ). Для добавленных подгрупп g проделаем то же самое, что и для f , только разбиение множества символов g проводим не по первой букве кодовых слов, а по второй. После этого в D добавятся новые группы, для них проводим разбиение по третьей букве кодовых слов и так далее. Подгруппы для g не добавляются (процесс прекращается), если хотя бы для одного символа ai Î g исчерпано кодовое слово wi . Покажем, что в результате действительно

получим r -дерево D Î Dr ( f ).

Предположим, что на очередном шаге получили неэлементарную группу g и необходимо разбить ее на подгруппы по l -ой букве кодового слова. Процесс останавливается, если некоторому символу ai Î g соответствует кодовое слово wi с длиной, меньшей l , то есть li < l . В силу неэлементарности g существует символ a j Î g , ai ¹ a j . По предыдущим построениям

первые l −1 букв в словах wi и wj совпадают, следовательно wi является началом слова wj , что противоречит префиксности кода. То есть для всех ai Î g выполнено li ³ l и разбиение по l -ой букве

провести можно. Процесс может остановиться только на элементарной группе. Разбиение g может быть тривиальным, то есть содержать g и пустые группы, если все l -ые буквы совпадают (при этом в r -дереве D появятся повторяющиеся группы, в частности, если g = {ai } и конец слова wi еще не

достигнут). В силу конечности кодовых слов через некоторое число шагов процесс закончится, причем будет ровно n начальных вершин {a1},K,{an} (повторяться начальные группы не могут, так

67

D Dr ( f ). Из каждой начальной вершины {ai } существует ровно один путь в f . Пройдем этот путь от конца к началу, последовательно выписывая буквы, соответствующие проходимым ребрам. Получим слово wi длины li , которая равна длине пути из {ai } в f . Если бы wi было началом слова wj , то

путь из {a j } в f содержал бы путь из {ai } в f , то есть вершина {a j } была бы подчинена {ai }, что невозможно. То есть получили префиксный код w1,K, wn . Утверждение доказано.

равна сумме вероятностей появления тех символов, которые входят в g , независимо от подгрупп, из которых организуется g . Тогда для любого r -дерева D = (V , E) D( f ) выполнено

P(D) = åg V \ND P(QD (g)) =åg V \ND åai g pi =p1l1 + K+ pnln , где

li – количество неначальных групп, в которые входит элемент ai , то есть длина пути из {ai } в f .

Таким образом, при функционале (2.1) стоимость P(D) r -дерева D , соответствующего префиксному коду, равна средней длине кодового слова. Следовательно, имея r -дерево минимальной стоимости на Dr ( f ) и пометив ребра некоторым образом, найдем оптимальный код, и обратно, имея оптимальный код, построим r -дерево D Dr ( f ) минимальной стоимости1. То есть задача об оптимальном дереве на Dr ( f ) с функционалом (2.1)

эквивалентна задаче об оптимальном алфавитном коде с входным алфавитом f = {a1,K, an}, набором вероятностей p1,K, pn и

выходным алфавитом {b1,K,br }.

1 Процедуры построения дерева по коду и кода по дереву описаны в доказательстве утверждения 2.2.

68

На рис. 2.4 приведен пример оптимального префиксного кода с входным алфавитом {a, b, c,d}, вероятностями появления символов 0,4; 0,3; 0,2; 0,1 и выходным алфавитом {0,1}. Как видно из рисунка, длины путей (кодовых слов) равны 1, 2, 3, 3. Средняя длина пути, стоимость r -дерева и средняя длина кодового слова равны 1,9. Символу a , который встречается наиболее часто, соответствует кратчайшее кодовое слово 0. Остальным – более длинные кодовые слова. Если бы вероятности появления всех

Рис. 2.4. Оптимальный бинарный код и соответствующее 2-дерево.

Разработанные в главе III общие алгоритмы поиска оптимального r -дерева могут быть использованы для построения оптимальных кодов. Разумеется, в теории кодирования созданы гораздо более эффективные алгоритмы: для r = 2 – это алгоритм Хаффмана построения оптимального бинарного кода [48], для произвольного r ³ 2 обобщение алгоритма Хаффмана описано, например, в [42]. Алгоритмы имеют порядок сложности n log n и

позволяют, таким образом, решать задачи на Dr ( f ) для функционала (2.1).

Утверждение 2.3. Функционал (2.1) вогнут. Доказательство. Рассмотрим набор групп {g1,K, gk } и

произвольное разбиение на поднаборы {h1,K, hi } и {hi+1,K, hk }

(см. опр. 1.30), k ³ 3, 1 < i < k . Обозначим g = g1 K gk , h = h1 K hi . Тогда g = h hi+1 K hk , то есть P(g1,K, gk ) = = åai g pi = P(h, hi+1,K, hk ). Следовательно, верно неравенство

P(g1,K, gk ) ≤ P(h1,K, hi ) + P(h,hi+1,K, hk ) . Утверждение доказано.

Таким образом, по следствию к теореме 1.6 оптимальным деревом на D( f ) будет веерная организация стоимости 1. Она же

69

будет оптимальной на Dr ( f ) при r ³ n , так как в этом

тривиальном случае каждому символу входного алфавита соответствует слово из одной буквы выходного алфавита.

3. Оптимальная структура управления сетью доставки материальных потоков.

В различных работах (см., например, [10, 37]) приводится следующая задача1. Задана сеть доставки материальных потоков T = (N, ET ), то есть ориентированный граф с множеством вершин N и дуг ET , связывающий источники материальных потоков с потребителями через промежуточные точки ветвления. Каждая

дуга (u,v) ET характеризуется потоком заявок частоты π (u,v) на материальные потоки и величиной материального потока ϕ(u,v).2

материальный поток ϕ(h) , с которыми “имеет дело” центр,

обозначены поток заявок и материальный поток из группы g′ в группу g′′. Таким образом, через центр, управляющий группой h , проходит поток заявок из h во все остальные элементы N (первое слагаемое), из всех остальных элементов N в h (второе слагаемое) и потоки заявок между подгруппами из QD (h), которые

непосредственно подчинены группе h (третье слагаемое). То же самое касается и материальных потоков. Общие потери (затраты), связанные с работой системы управления, определяются

1С точностью до обозначений.

2Сеть представляет собой частный случай технологического графа (см. п.1), но функционал стоимости определяется по-другому.

70