Оптимальные иерархические структуры - Воронин А.А., Мишин С.П

содержится в поддереве с корнем в h2 . Если s1 ¹ Æ, s2 ¹ Æ , то

λ(g,s) = λ(h1,s1 ) + λ(e1 ) + λ(h2 ,s2 ) + λ(e2 ). Если s1 = Æ, s2 ¹ Æ , то

λ(g,s) = λ(g,{g}) = 0. Сравнив не более 2 s вариантов разбиения s на s1 и s2 , найдем минимальное значение λ(g,s). Для всех s L

сравним не более åi=1,m Cmi 2i < 3m вариантов.

Для вершин, из которых ребра не выходят, для любого s L известны λ(g,s) и соответствующие поддеревья. Будем говорить, что для таких вершин задача о поддеревьях решена. В силу ацикличности H norm найдется g Vnorm , такая что ребра из g идут в вершины, для которых задача о поддеревьях решена. Тогда решим задачу для g , что потребует менее 3m сравнений весов поддеревьев. И так далее, в итоге решим задачу для всех вершин g Vnorm . Тогда λ( ,f ) и соответствующее поддерево являются искомыми, что и доказывает теорему.

Следствие 1.1 Для структурного функционала общего вида существует алгоритм, решающий задачу об оптимальной

последовательной организации путем сравнения менее (n +1)2n3m

весов поддеревьев графа H norm = (Vnorm , Enorm ).

Доказательство. Для любой вершины g VH графа задачи

выходит n − j ребер. Для всех вершин мощности один добавим в H norm не более åj=1,n−1 2(n - j) вершин. Для вершины добавим

1Следствие 2 будет доказано ниже в пункте 3 §2.

2Из вершин мощности n − 2 и n − 1 выходит не более двух ребер, следовательно для них дополнительные вершины в H norm не добавляются.

151

iCni = nCni−−11, оценим последнее выражение величиной n2n . Так как VH = 2n, то V2 (Hnorm) ≤ Vnorm ≤ (n +1)2n, что и доказывает следствие.

Доказательство теоремы 4.2 дает алгоритм поиска оптимальной на Op (f ) последовательной организации

произвольного набора групп f для структурного функционала общего вида. Пример найденной алгоритмом оптимальной организации приведен на рис. 5.3.

Следствие 1 дает верхнюю оценку сложности в худшем случае. Вершины графов H и H norm , которые не вложены ни в

одну из групп набора f = { f1,K, fm }, не могут входить ни в одно

поддерево, так как все листья поддерева содержатся среди групп набора f . Таким образом, при поиске оптимального поддерева можно рассматривать не весь граф H norm , а только те его

вершины, которые вложены хотя бы в одну из групп набора f . С учетом этой оговорки, оценим сложность в среднем следующим образом.

Таблица 4.1. Оценка сложности алгоритма в среднем.

Сгенерируем случайным образом набор групп. Каждый элемент входит в группу с вероятностью 0,5. Вычислим количество вершин графа H norm , из которых выходит два ребра и

которые вложены хотя бы в одну из групп набора f . По теореме 4.2 оценим сложность в среднем по 100 тестам. Результат приведен в таблице 4.1. В строках приведены значения для различных m от 2 до 20. В столбцах – для различных n от 4 до 15. Если m, n ≤ 15, то сложность остается приемлемой.

152

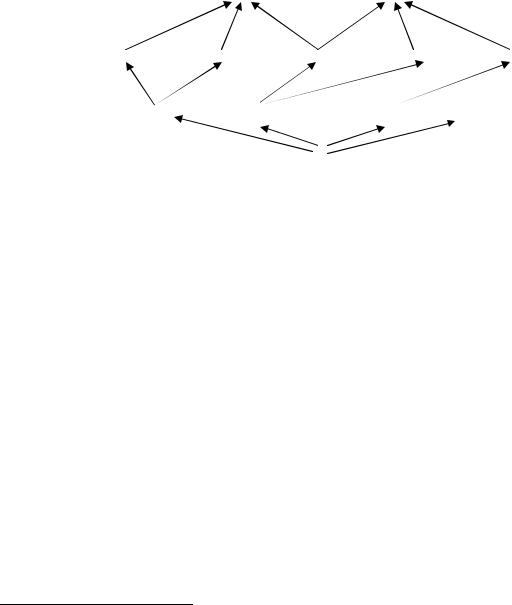
Рассмотрим пример, поясняющий материал данного параграфа. Решим задачу об оптимальной на Op (f ) последователь-

группы не являются подмножествами ни f1, ни f2 . Интересующая нас часть графа H изображена на рис. 4.3.

Согласно теореме 4.1, имея оптимальное поддерево H с корнем в и листьями в f1 и f2 , построим соответствующую ему

оптимальную последовательную организацию. Предположим, что веса всех ребер, кроме нижних, равны единице (все значения функционала равны единице). Тогда вес поддерева равен числу входящих в него ребер, не считая нижних. Очевидно, что в любое поддерево входят не менее трех таких ребер. В поддерево

D = (VD , ED ) с множеством вершин VD = { ,{a2},{a2 , a3}, f1, f2} входят ровно три таких ребра, то есть оно оптимально. Вес D равен трем (λ(D) = 3). Построим соответствующую оптимальную

организацию G такой же стоимости2. Граф G содержит един- ственную промежуточную вершину {a2 , a3}, которая используется

как для организации f1, так и для организации f2 (см. рис. 4.4).

1Напомним, что под поддеревом подразумевается поддерево с корнем в , содержащее неэлементарные группы набора f , листья которого содержатся среди неэлементарных групп набора f .

2Процедура построения последовательной организации по поддереву графа задачи H описана в доказательстве теоремы 4.1.

153

{a1, a2 , a3} {a2 ,a3 ,a4} {a2 , a3}

{a1} {a2} {a3} {a4}

Рис. 4.4. Оптимальная последовательная организация.

В общем случае оптимальное поддерево H строится с помощью нормализации графа. В примере на рис. 4.3 только из вершины выходит более двух ребер. Следовательно, при

нормализации будут добавлены две вершины g11 и g12 , в которые будут идти ребра из . Из g11 будут идти два ребра в {a1} и {a2}, из g12 – два ребра в {a3} и {a4} (см. опр. 4.4). По утверждению 4.1 поддереву D в H соответствует одно и только одно поддерево D′

вH norm такой же стоимости (например, если ребро ( ,{a1}) входит

вD , то вместо него в D′ входит путь ( , g11), (g11,{a1}) и наоборот). Задачу об оптимальном поддереве в H norm решает алгоритм

ребер (см. рис. 4.3), задача о поддеревьях решена: λ( f1,{ f1}) = 0 ,

λ( f2 ,{ f2}) = 0 , остальные значения равны + ∞ , так как поддерев- ом с корнем f1 можно покрыть только вершину f1 (то же верно и для f2 ). Решим задачу о поддеревьях с корнем в {a2 , a3}. Найдем

λ({a2 , a3},{ f1, f2}) следующим образом. Из {a2 , a3} выходят два ребра в вершины f1 и f2 . Часть набора { f1, f2} должна покры- ваться деревом с корнем f1, оставшаяся часть – деревом с корнем f2 . Очевидно, что единственный вариант разбиения { f1, f2}, стоимость которого не равна + ∞ , использует поддеревья,

поддеревьях для {a2 , a3} будет решена. Для остальных вершин H norm задача о поддеревьях решается аналогично.

154

§2. Оценка сложности задачи при функционале вида P( g1 ,K, gk , g ). Алгоритм решения.

1. NP -полнота задачи.

В случае функционала вида P( g1 ,K, gk , g ) оценим объем начальных данных задачи об оптимальной на Op (f )

элементов. Во-вторых, значения функционала. Для оценки их количества введем следующее обозначение.

= P( j,1, j +1).

Величина Pj зависит только от мощности j группы g , а не от самой группы или от элементарной подгруппы {a}. То есть обозначение корректно. Для любой организации G = (V, E) Op (f)

стоимость последовательной организации влияют лишь величины P1,K, PM −1, где M ≤ n – максимальная из мощностей групп набора

непустых подмножеств N .

2 Согласно замечаниям, сделанным в начале главы, рассматриваются последовательные организации без повторяющихся групп, следовательно любая неэлементарная группа h организуется из подгрупп g и {a}, {a} g .

155

множеству представителей минимальной мощности соответствует оптимальная на Op (f ) организация и наоборот. Для этого

построим процедуры перехода от множества представителей к организации из Op (f ) и обратно.

соответствующие ребра. В результате по q -элементному

мощности два в G . Рассмотрим g = {as , at } V , 1 ≤ s < t ≤ n. Из g

157

Обозначим решение задачи об оптимальной на Op (f )

организации через G , P(G) = qP1 + mP2 . После этого согласно пункту b) за полиномиальное время найдем множество представ-

оптимальной на Op (f ) организации, за полиномиальное время решим задачу о представителях в 2-множествах. Теорема доказана.

Кратко идею доказательства теоремы можно пояснить

организаций из Op (f ) может изменяться за счет числа

промежуточных групп мощности два. Построено соответствие,

при котором каждая такая группа определяет элемент некоторого множества представителей и наоборот, что и показывает эквивалентность задачи о представителях в 2-множествах и задачи об оптимальной последовательной организации.

Итак, если P ¹ NP , то не существует полиномиального алгоритма решения задачи на Op (f ), даже если мощности всех

групп набора f не превосходят трех. Следующие пункты посвя- щены модификации построенного в §1 алгоритма для функционал- ов вида P( g1 ,K, gk , g ) . Такая модификация позволяет снизить

сложность, пользуясь особым видом функционала.

2. Узловые группы.

В данном пункте доказываются утверждения, позволяющие для функционала вида P( g1 ,K, gk , g ) анализировать не все организации из Op (f ), а лишь организации, удовлетворяющие условиям утверждений 4.2 и 4.3. Опираясь на этот факт, в пункте 3

158

модифицируется алгоритм решения задачи на Op (f ) для функционалов вида P( g1 ,K, gk , g ) .

Определение 4.5.Назовем узловыми группами группы множ-

ества U ={fi1 ÇKÇ fik :1£ k £ m,1£ i1 <K< ik £ m}\{{a1},K,{an},Æ}.

То есть под узловыми группами будем понимать неэлемен- тарные группы, которые являются пересечением каких-либо групп набора f = { f1,K, fm }. В частности, неэлементарные группы

набора f принадлежат U . В примере (см. рис. 4.3) узловыми будут группы f1 = {a1, a2 , a3}, f2 = {a2 , a3 , a4} и {a2 , a3} = f1 Ç f2 .

Утверждение 4.2. Для функционала вида P( g1 ,K, gk , g ) существует оптимальная на Op (f ) последовательная организация G , в которой любая вершина g с двумя или более выходящими ребрами ( RG (g) ³ 2) является либо узловой, либо элементарной.

Доказательство. Пусть G = (V , E) – некоторая оптимальная на Op (f ) организация. Пусть из g ÎV \ NG , g U выходят по

крайней мере два ребра в h1 и l1, причем из g не существует пути ни в одну вершину, обладающую такими же свойствами. Через h1 - h2 -K- hn1 обозначим путь из h1 в “ближайшую” узловую

группу hn1 ÎU . Через l1 - l2 -K- ln2 обозначим путь из l1 в “ближайшую” узловую группу ln2 ÎU . То есть единственными

узловыми вершинами обоих путей будут последние вершины. Такие пути существуют, так как все неэлементарные терминальные вершины графа G содержатся в наборе f , то есть являются узловыми.

Тогда g′ U и выполнено строгое вложение g g′, так как g U .

159

результате получим последовательную организацию G¢ Op (f) .

вершин, так как в противном случае общая вершина организовыв- алась бы из неэлементарных подгрупп, что противоречит определению последовательной организации. Вместо вершин h1,K,hk и l1,K,lk в G′ входят вершины g1,K, gk такой же мощности. То есть P(G′) ≤ P(G) . Мы не добавили в G′ ни одной

неузловой вершины, из которой выходило бы более одного ребра. Из g в G′ выходит на одно ребро меньше, чем в G . Проделываем

вышеперечисленные действия до тех пор, пока из g не будет выходить одно ребро. В результате построим оптимальную на Op (f ) организацию, в которой число неузловых неэлементарных

вершин с более чем одним выходящим ребром на одну меньше, чем в G . Продолжая такие действия, получим искомую оптим- альную последовательную организацию. Утверждение доказано.

Утверждение 4.3. Для функционала вида P( g1 ,K, gk , g ) существует оптимальная на Op (f ) организация G , удовлетворя- ющая утверждению 4.2 и следующим условиям:

a)если в G найдется путь из узловой вершины g1 в узловую

вершину g2 , не содержащий других узловых вершин, то в U не существует “промежуточной” узловой группы g3 U , g1 g3 g2;

b)если в G узловой вершине g2 не подчинена никакая другая узловая вершина, то в U не существует “вложенной”

узловой группы g3 U , g3 g2 .

Доказательство. Рассмотрим оптимальную на Op (f )

160