
Оптимальные иерархические структуры - Воронин А.А., Мишин С.П
.pdf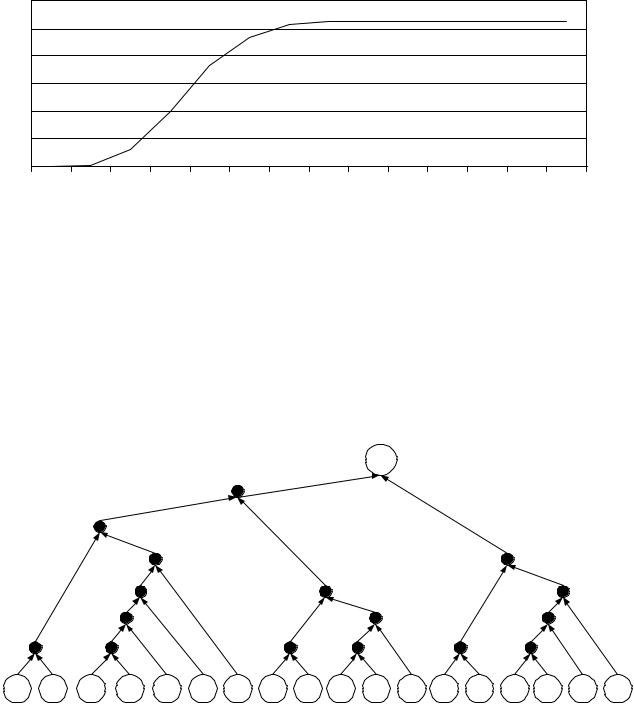
r |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
s(15,r) / q(15,r) |
435 |
74 |
28 |
15 |
10 |
8.7 |
7.9 |
7.6 |
7.6 |
7.6 |
7.6 |
7.6 |
7.6 |
7.6 |
Таблица 3.4. Отношение сложности переборного алгоритма поиска r -дерева s(n,r) к минимально возможной сложности точного алгоритма q(n, r) при n =15.
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Рис. 3.3. Сложность s(15, r) переборного алгоритма поиска r -дерева при 2 ≤ r ≤ 15.
Рис. 3.3 показывает, что при росте r от 2 до n сложность переборного алгоритма поиска оптимального r -дерева быстро возрастает примерно до r = n / 2, после чего остается практически неизменной, близкой к s(n) (см. таблицу 3.2). То есть сложность
s(n / 2,n) переборного алгоритма при n > 20 неприемлемо высока.
f
a10 |
a11 |
a1 |
a2 |
a3 |
a6 |
a12 |
a13 |
a14 |
a7 |
a8 |
a15 |
a16 |
a17 |
a4 |
a5 |
a9 |
a18 |
Рис. 3.4. Оптимальное на D2 ( f ) 2-дерево организации группы f = {a1,K,a18}.
Приведем пример найденного алгоритмом оптимального на D2 ( f ) 2-дерева организации группы f = {a1,K, a18} из
111

восемнадцати элементов |
(n = 18) для функционала (IV) с |
функцией сложности вида (2.2) (см. §2 гл. II). Для примера |
|
положим α = 1 и β = 0.5, |
то есть рассмотрим точку из области, в |
которой функционал не является ни выпуклым, ни вогнутым (см. рис. 2.8). Сложности элементов определим следующим образом
C(a1) = 1,C(a2 ) = 2,K,C(a18 ) = 18. |
Оптимальное |
2-дерево |
изображено на рис. 3.4. |
|
|
3. Оценка сложности задачи на D( f ) при функционале вида P( g1 ,K, gk , g ) . Алгоритм решения.
Как было отмечено в начале главы, если функционал имеет вид P( g1 ,K, gk , g ) , то стоимость организации подгрупп в группу
зависит только от их мощностей, но не от состава. То есть варианты разбиения g на подгруппы одинаковой мощности имеют одинаковую стоимость. Приведем формальные определения.
Определение 3.1. Для любого нетривиального1 разбиения группы g на непересекающиеся подгруппы Q = {g1,K, gk }, k ³ 2,
g = g1 K gk вектором длин, соответствующим набору Q , назовем вектор v = (v1,K,v g −1) , i -я компонента vi которого равна
количеству подгрупп мощности i , входящих в Q , i = 1, g −1.
Определение 3.2. Два нетривиальных разбиения Q1 и Q2 группы g назовем существенно различными, если различаются векторы длин, соответствующие Q1 и Q2 .
Если наборы Q1 = {g1,K, gk } |
и Q2 |
|
= {h1,K, hk }, |
g = g1 K |
||||||||||||||
gk = h1 K hk не являются |
существенно различными, то |
|||||||||||||||||
очевидно, что наборы чисел |
|
g1 |
|
,K, |
|
gk |
|
и |
|
h1 |
|
,K, |
|
hk |
|
|
одинаковы с |
|
|
|
|
|
|
|
|
|
|||||||||||
точностью до перестановки, следовательно выполнено соотношение P(Q1) = P( g1 ,K, gk , g ) = P( h1 ,K, hk , g ) = P(Q2 ) .
Таким образом, при поиске оптимального дерева переборными алгоритмами (см. утв. 3.2 и 3.4) можно анализировать не все
1 То есть группа разбивается на две или более подгруппы.
112
разбиения, а лишь те, которые существенно различны. Перефор- мулируем пункт 1 для функционала вида P( g1 ,K, gk , g ) .
Через q~(n,r) обозначим количество способов нетривиального разбиения группы из n элементов на существенно различные наборы из r или менее подгрупп, n ³ 2, r ³ 2. Через q~(n) = q~(n, n)
обозначим общее число способов нетривиального разбиения группы из n элементов на существенно различные наборы
подгрупп. |
Очевидно, |
что |
для |
|
любого |
r > n |
выполнено |
|||||||||
q(n, r) = q(n, n) = q(n), |
так |
как |
|
нельзя разбить группу |
из n |
|||||||||||
~ |
|
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|||
элементов более чем на n непересекающихся подгрупп. |
|
|||||||||||||||
|
|
Утверждение 3.5. Алгоритм, решающий задачу об |
||||||||||||||
оптимальном дереве на D( f ), |
|
f |
|
= n ³ 3 с функционалом |
вида |
|||||||||||
|
|
|||||||||||||||
P( g1 ,K, gk , g ) , |
должен |
проанализировать |
не |
менее |
q(n) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
значений функционала P. Любой алгоритм, анализирующий менее |
||||||||||||||||
q(n) |
значений P, |
может выдать |
|
решение, стоимость которого |
||||||||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сколь угодно больше стоимости оптимального дерева. Доказательство. Зададим функционал P′(g1,K, gk ) стоимо-
сти организации подгрупп g1,K, gk в группу |
|
g = g1 K gk |
|||
следующим образом: |
|
ì0, при g ¹ f |
|
||
(3.4) |
P¢( g1 |
, |
|||
,K , g k ) = í |
f |
||||
|
|
î y, при g = |
|
||
где y > 0 – произвольное число.
Тогда любое дерево D D( f ) имеет стоимость y . Предполо- жим, что алгоритм, решающий задачу об оптимальном дереве на D( f ), анализирует менее q~(n) значений P. Применим его для решения задачи с функционалом P¢. Обозначим полученное дерево через D′ D( f ) . Найдется такой набор подгрупп h1,K, h j ,
f = h1 K hj , что все варианты организации f , стоимость которых проанализирует алгоритм, будут существенно отличаться
от h1,K, h j . Если в D¢ |
набор QD′ ( f ) существенно отличается от |
|||||||
h1,K, h j , то зададим функционал P¢¢ следующим образом: |
||||||||
|
|
ì0, при g ¹ f или при |
k = j |
и несуществе нном |
||||
(3.5) |
P¢¢(g1,K, gk ) = |
ï |
различии g |
,K, g |
|
и h ,K ,h |
|
|
í |
k |
j |
||||||
|
|
ï |
1 |
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
î y, в противном случае |
|
|
||||
113

Если в D′ набор QD′ ( f ) |
не отличается существенно от h1,K, h j , |
||
то, выбрав произвольное |
z > y , зададим функционал P′′ следую- |
||
щим образом: |
ì0, при g ¹ f |
|
|
|
|
|
|
(3.6) |
|
ïz, при k = j |
и несуществе нном |
P¢¢(g1,K, gk ) = í |
,K, gk и h1,K,hj |
||
|
|
ïразличии g1 |
|
|
|
ï |
|
|
|
îy, в остальных случаях |
|
Применим алгоритм для решения задачи с функционалом P′′.
Мы изменили значения функционала только для тех вариантов организации f , которые несущественно отличаются от h1,K, h j 1.
Эти значения алгоритм не анализировал. Следовательно, в качестве решения опять будет выдано дерево D′.
При первом варианте выбора P′′ деревья из D( f ), в которых
группа f |
организуется из |
подгрупп |
h1,K, h j , |
имеют |
нулевую |
|
стоимость, а P(D ) = y . |
|
|
|
|
|
|
|
′ |
|
|
|
|
|
При |
втором варианте |
выбора |
P′′ в |
силу |
n ³ 3 |
в D( f ) |
существует по крайней мере одно дерево, |
в котором группа f |
|||||
организуется из набора подгрупп, существенно отличающегося от h1,K, h j . Стоимость такого дерева равна y , а P(D′) = z .
В обоих случаях стоимость выданного решения может быть сколь угодно большей, чем стоимость оптимального дерева. Утверждение доказано.
Лемма 3.3. Если функционал имеет вид P( |
g1 |
,K, |
gk |
, |
g |
) и |
|||
при каждом i = |
|
|
для некоторой группы g мощности i |
известно |
|||||
2,n |
|||||||||
ее разбиение Q(g) |
в некотором оптимальном дереве Dg D(g) |
||||||||
организации |
g , то можно построить оптимальное на D( f ) дерево |
||||
организации |
f , |
|
f |
|
= n , не вычисляя значений функционала |
|
|
||||
стоимости.
Доказательство. Для группы мощности два существует единственное дерево организации, построить которое можно, не
1 Изменить значение функционала только на наборе подгрупп h1 ,K, h j нельзя, так как P имеет вид P( g1 ,K, gk , g ) и при изменении стоимости P(h1 ,K, h j )
автоматически изменится стоимость всех вариантов, которые несущественно отличаются от h1 ,K, h j .
114

вычисляя P . Введем индуктивное предположение, что для всех групп мощности меньше s можно построить оптимальные деревья их организации без вычисления P (2 < s ≤ n).
Рассмотрим произвольную группу h = {al |
,K, al |
} мощности |
1 |
s |
|
s . Известно некоторое разбиение Q1 = {g1,K, gk } группы g мощ- |
||
ности s в оптимальном дереве Dg D(g) . Обозначим мощности
групп g1,K, gk |
через j1,K, jk , |
j1 +K+ jk |
= s. |
Построим |
||||||||||
разбиение группы h на подгруппы |
Q2 = {h1,K, hk } следующим |
|||||||||||||
образом: h1 ={al ,K,al |
j1 |
},h2 ={al |
j1+1 |
,K,al |
},…,hk ={al |
j1+K+ jk |
−1+1 |
,K,al }. |
||||||
1 |
|
|
|
j1+ j2 |
|
|
|
s |
||||||
То есть отнесем к подгруппе h1 первые j1 элементов h , |
ко второй |
|||||||||||||
– следующие j2 |
элементов h , и т. д. Наборы Q1 и Q2 не являются |
|||||||||||||
существенно различными, следовательно P(Q1) = P(Q2 ). |
|
|
|
|
||||||||||
Мощность групп h1,K, hk меньше s , следовательно |
по |
|||||||||||||
индуктивному предположению |
для каждой |
h j , |
|
j = |
|
можем |
||||||||
|
1, k |
|||||||||||||
построить оптимальное дерево организации |
h j , |
не вычисляя |
P. |
|||||||||||
Стоимость такого дерева будет равна стоимости оптимального
дерева организации g j в силу |
|
g j |
= |
h j |
. Тогда можно построить |
||||
дерево |
Dh D(h) организации |
|
h , проведя в h ребра из корней |
||||||
оптимальных |
деревьев |
организации групп h1,K, hk . Имеем |
|||||||
P(Dh ) = P(Dg ) |
в силу |
равенства |
стоимостей |
поддеревьев и |
|||||
условия |
P(Q1) = P(Q2 ). |
То |
есть, |
опираясь |
на индуктивное |
||||
предположение, построили оптимальное дерево организации группы h , не вычисляя P. В итоге по индукции доказана возможность такого построения для группы мощности n , то есть
для |
f . Лемма доказана. |
|
|
|
|
|
||||||||||||
|
|
|
Доказательство следующего утверждения дает алгоритм |
|||||||||||||||
поиска оптимального дерева на D( f )1 |
с функционалом вида |
|||||||||||||||||
P( |
|
g1 |
|
,K, |
|
gk |
|
, |
|
g |
|
) и его сложность. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Утверждение 3.6. Существует алгоритм, решающий задачу |
|||||||||||||||
об |
оптимальном дереве организации |
на D( f ), |
|
f |
|
= n с |
||||||||||||
|
|
|||||||||||||||||
1 Аналогичным образом строится алгоритм поиска оптимального на Dr ( f ) дерева с уровнем не более L (см. сноску перед утв. 3.2).
115

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
функционалом |
вида |
|
P( |
g1 |
,K, |
gk |
, |
g |
) |
за |
s (n) = å |
|
q(i) |
|||||||
вычислений P. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=2,n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство. Предположим, что для |
фиксированного |
|||||||||||||||||||
2 ≤ i ≤ n |
при |
каждом |
j = |
|
|
для |
некоторой |
группы |
|
g j |
||||||||||
1,i −1 |
|
|||||||||||||||||||
мощности |
j известно ее разбиение Q(g j ) в некотором оптималь- |
|||||||||||||||||||
ном дереве Dg j |
D(g j ) |
организации g j |
и стоимость этого дерева |
|||||||||||||||||
P(Dg j ).1 |
Рассмотрим |
некоторую |
группу |
gi |
мощности |
i |
и |
|||||||||||||
проанализируем все |
q(i) |
вариантов существенно |
различного |
|||||||||||||||||
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
разбиения gi на подгруппы. |
|
|
|
|
|
gi |
|
|
|
|
|
|||||||||
Пусть в |
очередном |
варианте |
|
группа |
разбивается |
на |
||||||||||||||
подгруппы Q′(gi ). Мощность подгрупп из Q′(gi ) не более i −1. По
предположению для подгрупп такой мощности известна стоимость оптимального дерева организации (стоимость оптимальных
деревьев организации всех подгрупп одинаковой мощности одинакова в силу вида функционала). Вычислим P(Q′(gi )),
прибавим стоимости оптимальных деревьев организации подгрупп из Q′(gi ). Получим стоимость некоторого дерева организации gi .
В оптимальном дереве D* D(gi ) группа gi организуется из некоторых подгрупп h1,K, hk . Будет проанализировано разбиение Q′(gi ) группы gi , которое несущественно отличается от h1,K, hk . Тогда P(h1,K, hk ) = P(Q′(gi )) , соответствующие подгруппы в наборах Q(gi ) и h1,K, hk имеют одинаковую мощность. Следовательно, стоимость оптимального на D(gi ) дерева и соответствующее ей разбиение Q′(gi ) будут найдены алгоритмом. Что позволяет перейти к следующему значению i .
Для каждого i = 2, n вычислим функционал стоимости q~(i) раз. В итоге, вычислив ~s (n) значений P, при каждом i = 2, n для некоторой группы gi мощности i найдем ее разбиение Q(gi ) в некотором оптимальном дереве Dgi D(gi ) . После этого по лемме 3.3 построим оптимальное дерево организации f без
1 При минимальном i = 2 предположение очевидно выполнено, так как
оптимальное дерево организации элементарной группы состоит из одной изолированной вершины и имеет нулевую стоимость.
116
дополнительных |
вычислений |
функционала |
стоимости. |
Утверждение доказано. |
|
|
|
Поясним определения 3.1 и 3.2, утверждения 3.5 и 3.6 на |
|||
примере (см. рис. |
3.1). Три варианта разбиения |
f = {a1, a2 ,a3}, |
|
изображенные слева, не являются существенно различными, так как в них f разбивается на подгруппу мощности 1 и подгруппу мощности 2 (всем вариантам соответствует один и тот же вектор длин (1,1)). Стоимости соответствующих деревьев равны. Поэтому все три варианта анализировать не нужно, достаточно выбрать любой из них. Кроме того, необходимо вычислить стоимость организации f при разбиении, изображенном справа (см. рис. 3.1). Ему соответствует вектор (3,0), и этот вариант существенно отличается от всех остальных. Всего при анализе разбиений f вычислим q~(3) = 2 значения функционала. Согласно утверждению 3.5 это минимально возможное количество вычислений точным алгоритмом. Еще q~(2) = 1 раз вычислим функционал для
нахождения стоимости дерева организации группы мощности 2. Всего потребуется ~s (3) = q~(2) + q~(3) = 3 вычисления.
Алгоритм вычисления величины q~(n) . Через q~i, j
обозначим количество способов нетривиального разбиения группы
мощности |
i |
на существенно |
различные |
наборы |
подгрупп |
|||||||
|
|
|
|
|
|
|
|
|
~ |
|
|
|
мощности |
j |
или более, i = 1, n , j = 1,i , |
|
|
|
|||||||
qi,i = 0 . Предположим, что |
||||||||||||
для всех допустимых j |
|
|
|
|
|
|
~ |
~ |
~ |
|||
известны величины q1, j , |
q2, j ,…, |
qi−1, j . И, |
||||||||||
кроме того, |
известны |
величины |
~ |
|
~ |
,…, |
~ |
То есть |
||||
|
qi,i , |
qi,i−1 |
qi, j+1. |
|||||||||
известны те элементы матрицы (3.7), которые расположены выше
или правее элемента |
~ |
(все элементы |
на главной |
диагонали |
|||||
qi, j |
|||||||||
равны нулю). |
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
q1,1 |
~ |
|
|
|
|
|
|
|
|
~ |
|
|
|
|
||
|
|
|
q2,1 |
q2,2 |
~ |
|
|
|
|
(3.7) |
|
|
~ |
~ |
|
|
|
||
|
|
q3,1 |
q3,2 |
q3,3 |
|
|
|
||
|
|
|
. |
. |
. |
. |
|
|
|
|
|
|
~ |
~ |
. |
. |
~ |
|
|
|
~ |
|
qn,1 |
qn,2 |
qn,n |
|
|||
Тогда найдем |
следующим |
образом. |
Обозначим |
через k |
|||||
qi, j |
|||||||||
117
количество подгрупп мощности j , которое может содержать группа мощности i , чтобы мощность оставшейся части была нулевой или большей , чем j . Тогда имеем:
(3.8) |
|
ì0,K, ëi / jû -1, при i mod j ¹ 0 |
|
|
||
k = í |
|
|
|
|
||
|
|
î0,K,i / j - 2,i / j, при i mod j = 0 |
|
|
||
Поясним формулу (3.8). Если i не делится нацело на |
j , то в |
|||||
группе мощности i |
может содержаться не более ëi / jû подгрупп |
|||||
мощности |
j . Но |
если |
содержится ровно |
ëi / jû подгрупп, |
то |
|
мощность |
оставшейся |
части больше нуля |
и меньше |
j , |
что |
|
недопустимо. Таким образом, в первой строке (3.8) вычитаем 1 из
ëi / jû. Если i |
делится нацело на j , то в группе мощности i может |
||
содержаться |
от 0 |
до i / j подгрупп мощности j . Но |
если |
содержится |
i / j −1 |
подгруппа, то мощность оставшейся |
части |
равна j , что недопустимо. |
|
||
По формуле (3.8) выберем некоторое количество k подгрупп |
|||
мощности j . При |
k = 0 ни одной подгруппы мощности |
j не |
|
выбрано, следовательно “оставшуюся часть” мощности i
необходимо разбивать на подгруппы мощности |
j +1 или более. |
|||
Количество таких вариантов обозначим через |
~ |
|||
w(0) = qi, j+1 . При |
||||
k > 0 |
оставшуюся часть мощности |
i − kj можно вообще не |
||
разбивать или разбить на подгруппы мощности |
j +1 или более. |
|||
|
~ |
+1. |
Тогда можно записать |
|
Количество вариантов w(k) = qi−kj, j+1 |
||||
(3.9) |
~ |
|
по всем возможным |
|
qi, j = åk w(k) , где сумма берется |
||||
значениям k из соотношения (3.8). Равенство справедливо, так как любые наборы, содержащие разное количество подгрупп мощности j , существенно различны, и рассмотренными
вариантами исчерпываются все возможности разбиения группы мощности i на существенно различные наборы подгрупп мощности j или более.
Таким образом, в матрице (3.7) можно последовательно вычислить строки сверху вниз, вычисляя каждую из строк справа налево по формуле (3.9). Проведя вычисления в таком порядке, найдем все q~i, j . Тогда выполнено q~(n) = q~n,1. Алгоритм построен.
Значения q~(n) приведены в таблице 3.5. Из таблицы можно сделать вывод, что при увеличении n отношение q~(n) / q~(n −1)
118

уменьшается. Этот факт позволяет предположить, что порядок
минимальной сложности точного алгоритма меньше an для любого a > 1. То же самое можно сказать и про сложность ~s (n)
построенного алгоритма. Вопрос теоретического доказательства приведенной гипотезы остается открытым. Также открыт вопрос о
|
существовании полиномиальной по n оценки величин q(n) , s (n). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
~ |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
~ |
|
|
~ |
|
|
|
|
|
n |
|
|
~ |
|
|
~ |
|
|
|
|
|
|
|
|
n |
~ |
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
||||||||||
|
|
q(n) |
|
|
q(n) |
|
|
|
|
q(n) |
|
q(n) |
|
|
|
|
|
|
|
|
|
|
|
q(n) |
|
|
|
|
|
q(n) |
|
|||||||||||||||||||||||
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
||||
|
|
|
|
|
q(n −1) |
|
|
|
|
|
|
|
|
q(n −1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q(n −1) |
|
||||||||||||||||||
20 |
|
626 |
|
|
1.28 |
|
|
50 |
|
|
204 225 |
|
1.18 |
80 |
15 796 475 |
|
|
|
1.14 |
|
||||||||||||||||||||||||||||||||||
30 |
|
5 603 |
|
|
1.23 |
|
|
60 |
|
|
966 466 |
|
1.16 |
90 |
56 634 172 |
|
|
|
1.13 |
|
||||||||||||||||||||||||||||||||||
40 |
|
37 337 |
|
|
1.20 |
|
|
70 |
|
|
4 087 967 |
|
1.15 |
100 |
190 569 291 |
|
|
|
1.126 |
|
||||||||||||||||||||||||||||||||||
|
|
Таблица |
3.5. Минимальная сложность q(n) |
точного алгоритма поиска |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оптимального дерева на D( f ) при функционале вида P( |
|
g1 |
|
,K, |
|
gk |
|
, |
|
g |
|
). |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
n |
~ |
|
|
|
~ |
|
|
|
|
n |
|
~ |
|
|
~ |
|
|
|
|
|
|
n |
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
~ |
|
|
|
||||||||||||
|
s (n) |
|
|
s (n) |
|
|
s (n) |
|
s (n) |
|
|
|
|
|
|
|
|
|
|
|
|
s (n) |
|
|
|
|
|
|
s (n) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
||||
|
|
|
|
|
|
|
|
q(n) |
|
|
|
|
|
|
|
q(n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q(n) |
|||||||
|
20 |
2 693 |
|
4,30 |
|
|
50 |
|
|
1 295 920 |
|
|
6,35 |
|
|
|
|
|
80 |
123 223 558 |
|
|
7,80 |
|||||||||||||||||||||||||||||||
|
30 |
28 598 |
|
5,10 |
|
|
60 |
|
|
6 639 288 |
|
|
6,87 |
|
|
|
|
|
90 |
465 672 458 |
|
|
8,22 |
|||||||||||||||||||||||||||||||
|
40 |
215 267 |
|
5,76 |
|
|
70 |
|
|
30 053 883 |
|
|
7,35 |
|
|
|
|
|
100 |
1 642 992 467 |
|
|
8,62 |
|||||||||||||||||||||||||||||||
|
|
|
Таблица 3.6. Сложность s (n) алгоритма поиска оптимального дерева |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на D( f ) |
при функционале вида P( |
|
g1 |
|
,K, |
|
gk |
|
, |
|
g |
|
). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
Значения s (n) |
приведены в таблице 3.6. Из таблицы видно, |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
что |
построенный алгоритм имеет |
приемлемую |
сложность для |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
n ≤ 100. Кроме |
того, |
сложность |
алгоритма |
|
|
|
|
|
|
превосходит |
|||||||||||||||||||||||||||||||||||||||||||
минимально возможную сложность точного алгоритма не более, чем на порядок (~s (100) / q~(100) < 10). С другой стороны, нижняя оценка q~(n) сложности точного алгоритма неприемлемо высока при n существенно большем 100. Таким образом, имеет смысл построение эвристических алгоритмов, которые решают задачу с
приемлемой погрешностью для некоторых функционалов стоимости (см. §2).
Приведем пример найденного алгоритмом оптимального на D( f ) дерева организации группы f = {a1,K, a70} из семидесяти
элементов (n = 70) для функционала (II) с функцией сложности вида (2.2) (см. §2 гл. II). Для примера положим α = 0.5 и β = 1.5, то есть точку из области, в которой функционал не является ни выпуклым, ни вогнутым (см. рис. 2.6). Для того, чтобы функционал имел вид P( g1 ,K, gk , g ) , то есть зависел только от
119
мощностей подгрупп, сложности элементов должны быть равны: C(a1 ) = K = C(a70 ) . В силу однородности функционала масштаб
сложности не влияет на оптимальность организации. Положим сложности элементов равными единице: C(a1) = K = C(a70 ) = 1.
f
|
|
a21 |
a22 |
a23 |
a24 |
a29 |
a30 |
a31 |
a32 |
|
|
|
a56 |
a57 |
a58 |
a59 |
a60 |
a66 |
a67 |
68 |
a69 |
a70 |
a17 |
a18 |
a19 |
a20 |
a25 |
a26 |
a27 |
a28 |
|
|
a51 |
a52 |
a53 |
a54 |
a55 |
|
a61 |
a62 |
a63 |
a64 |
a65 |
|
|
|
|
a5 |
a6 |
a7 |
a8 |
a13 |
a14 |
a15 |
a16 |
|
a37 |
a38 |
a39 |
a40 |
|
a46 |
a47 |
48 |
a49 |
a50 |
a1 |
a2 |
a3 |
a4 |
a9 |
a10 |
a11 |
a12 |
|
a33 |
a34 |
a35 |
a36 |
a41 |
a42 |
a43 |
a44 |
a45 |
|
|
|
|
|
|
|
|
|
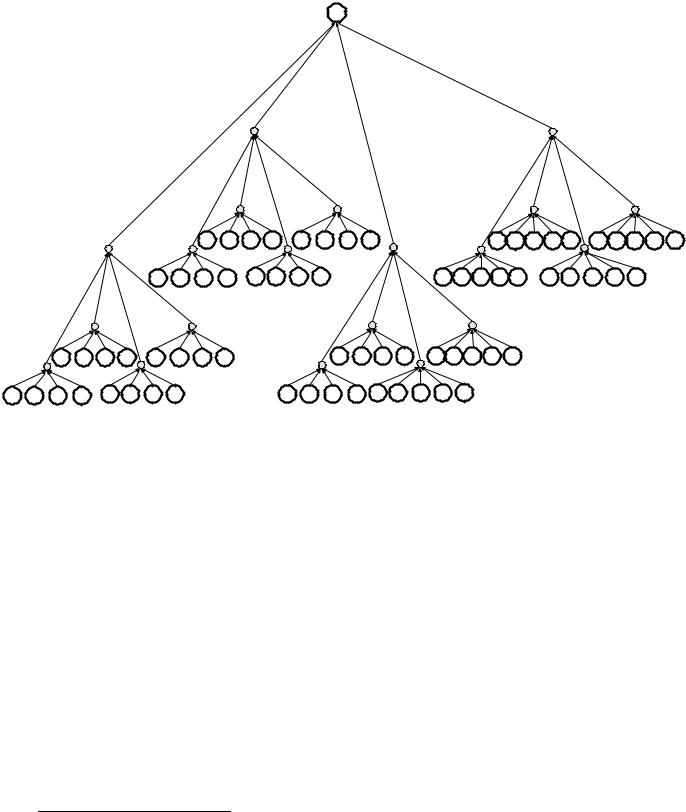
Рис. 3.5. Оптимальное на D( f ) дерево организации |
||||||||||||||
|
|
|
|
|
|
|
|
|
группы f |
= {a1,K, a70}. |
|
|
|
|
||||||
|
|
|
Оптимальное |
дерево |
изображено |
на |
рис. |
|
3.5. При n = 25, |
|||||||||||
|
|
n = 125 и n = 6251 оптимально симметричное 5-дерево, в котором |
||||||||||||||||||
|
|
каждая управляющая вершина имеет 5 подчиненных. При |
||||||||||||||||||
|
|
рассмотренном значении n = 70 элементы a1,K, a40 группируются |
||||||||||||||||||
|
|
в четверки, элементы a41,K, a70 |
группируются в пятерки. То есть |
|||||||||||||||||
все элементы подчиняются шестнадцати управляющим вершинам нижнего уровня, которые затем группируются в f с помощью симметричного 4-дерева.
При приближении β к единице функционал “приближается” к вогнутому и становится оптимальной веерная организация. При увеличении β становится оптимальной 2-организация (в
1 При n = 125 и n = 625 решение найдено эвристическим алгоритмом пункта 2 §2.
120
