Метод фазового контрасту

Оптична схема та сама, що і в методі темного поля. Приймаючи до уваги, що фон фокусується в точку, що лежить на осі в фокальній площині, а дифраговане світло (містить більш високі просторові частоти) відхиляється в сторону від фокуса, Церніке запропонував помістити в фокальній площині фазову пластинку, що міняє співвідношення фаз між сфокусованим і дифрагованим світлом. Фазова пластинка може представляти собою скляну підкладку, на яку нанесено маленьку плівку з прозорого матеріалу. Плівку поміщають в центр фокальної площини і має таку товщину і показник заломлення, що зміна фази сфокусованого світла по відношенню до зміни фази дифрагованого світла складає /2, або 3/2 рад. В першому випадку інтенсивність світла в площині зображення рівна:

а в другому випадку маємо

Таким чином, інтенсивність зображення стає лінійною функцією зсуву фази . Коли фаза на фазовій пластинці змінюється на /2, ми маємо позитивний фазовий контраст, а при зміні фази на 3/2 говорять про від’ємний фазовий контраст. Крім цього контраст можна покращити, якщо плівку зробити частково поглинаючою. Метод фазового контрасту — один з методів перетворення просторової фазової модуляції в просторову модуляцію інтенсивності. Товщину плівки прозорого однорідного матеріалу можна визначити з виразу:

Знак „+” береться для негативного фазового контрасту, а знак „–” для позитивного фазового контрасту. Діаметр пропускаючої області фільтра повинен бути дещо більшим діаметра плями сфокусованого не розсіяного випромінювання.

ЗАДАЧІ

Спроектувати просторовий фільтр для фільтрації лазерного пучка з довжиною хвилі 0.514мкм, що описується функцією Гауса, якщо його діаметр рівний 2,0 мм, а фокусна віддаль мікро-об’єктива рівна 13мм.
Спроектувати оптичну систему візуалізації фазових неоднорідностей методом негативного фазового контрасту з двома об’єктивами з фокусною відстанню кожний =150мм та апертурою 30мм. Довжина оптичної системи повинна бути 4 . Довжина хвилі 0.488мкм.
Спроектувати оптичну систему візуалізації фазових неоднорідностей методом темного поля з двома об’єктивами з фокусною відстанню кожний =200мм та апертурою 40мм. Довжина оптичної системи повинна бути 4 . Довжина хвилі 0.6328мкм.
Спроектувати оптичну систему візуалізації фазових неоднорідностей методом позитивного фазового контрасту з двома об’єктивами з фокусною відстанню кожний =300мм та апертурою 60мм. Довжина оптичної системи повинна бути 4 . Довжина хвилі 0.6328мкм.
Спроектувати корелятор спільного фур’є-перетворення, у якого другий каскад цифровий, фотоприймачем служить ПЗЗ-камери з розміром фото чутливого пікселя 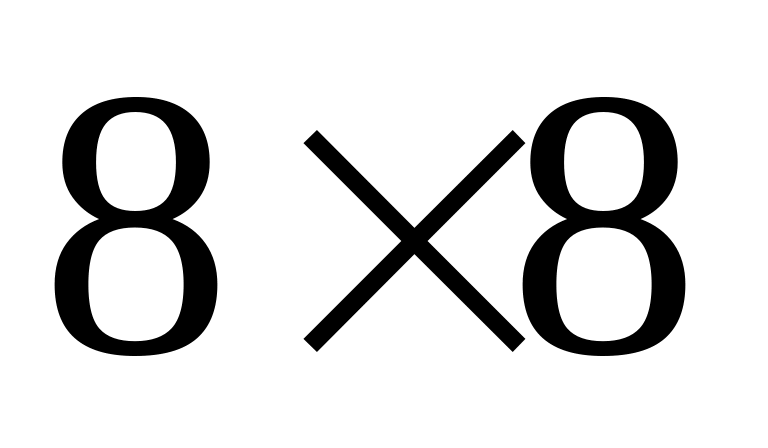мкм². Розміри еталонного зображення 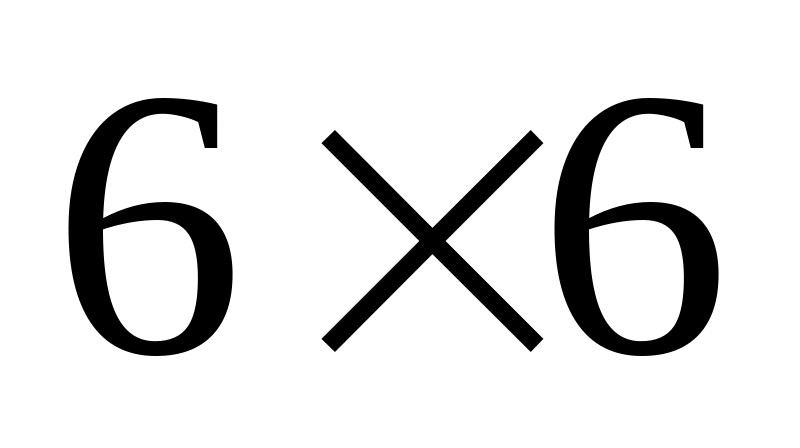мм² , а досліджуваного — мм². Камера має 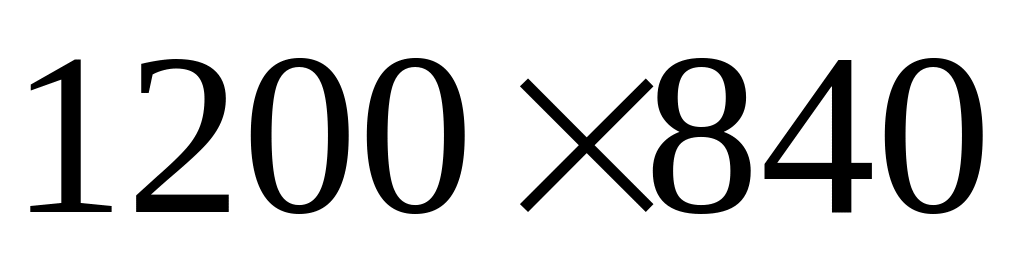пікселів. Як доповнити цифровий спектр Фур’є, щоб можна було реалізувати швидке фур’є-перетворення.

Відповіді та вказівки до розв’язку задач з топоСу Періодичні функції і розклад їх в ряд Фур’є

.
,
.
.
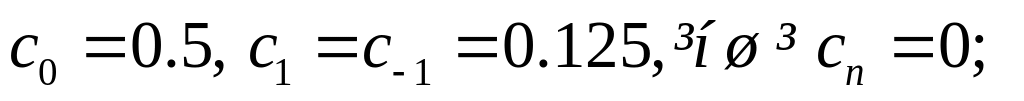
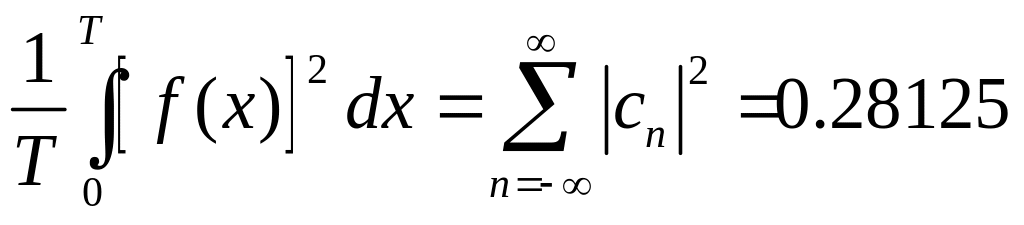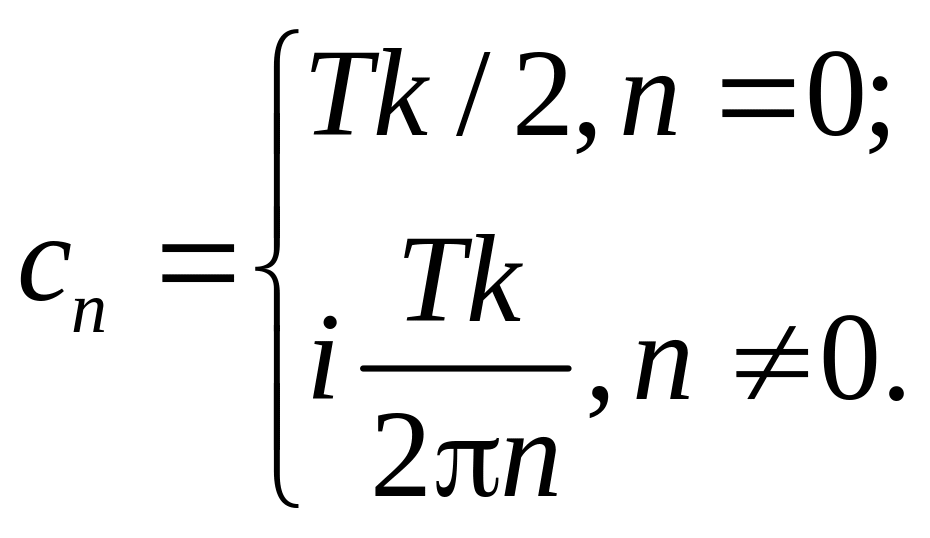
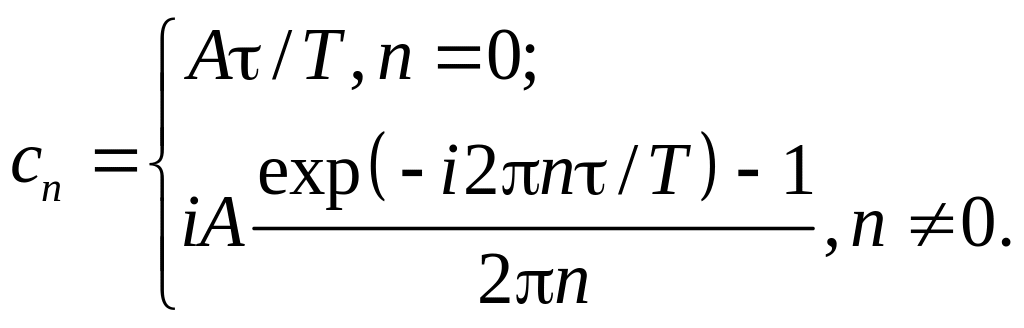
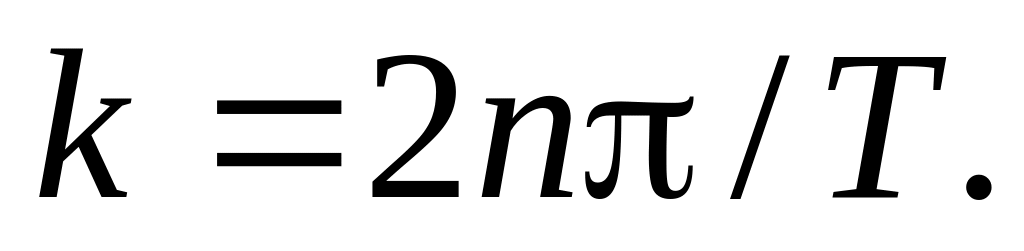
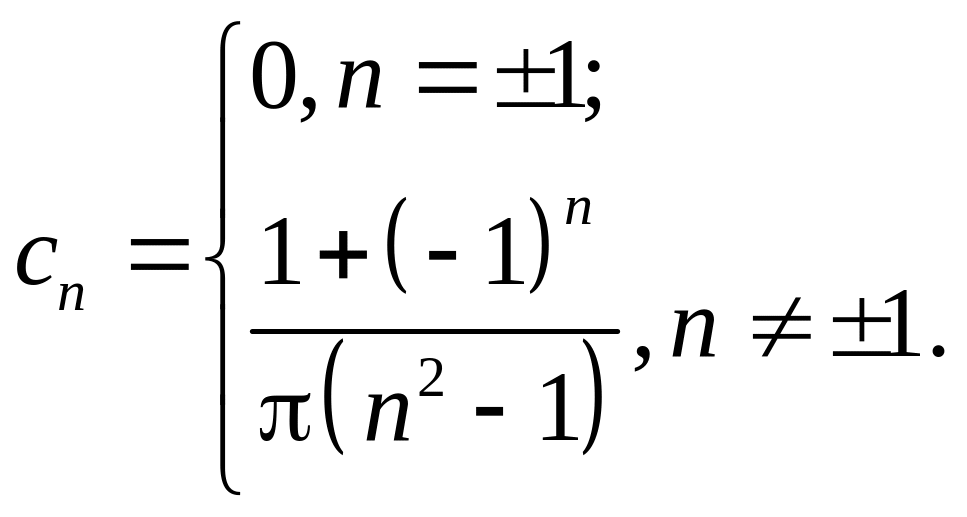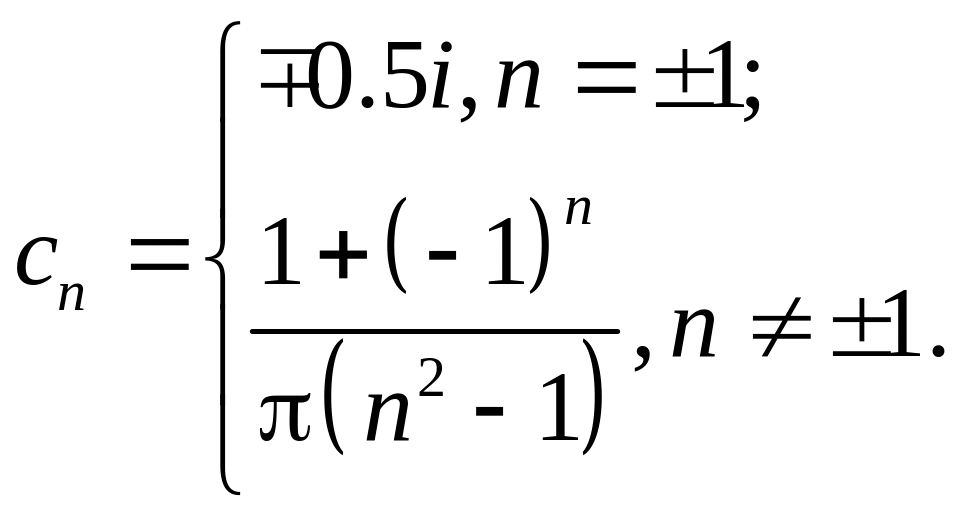
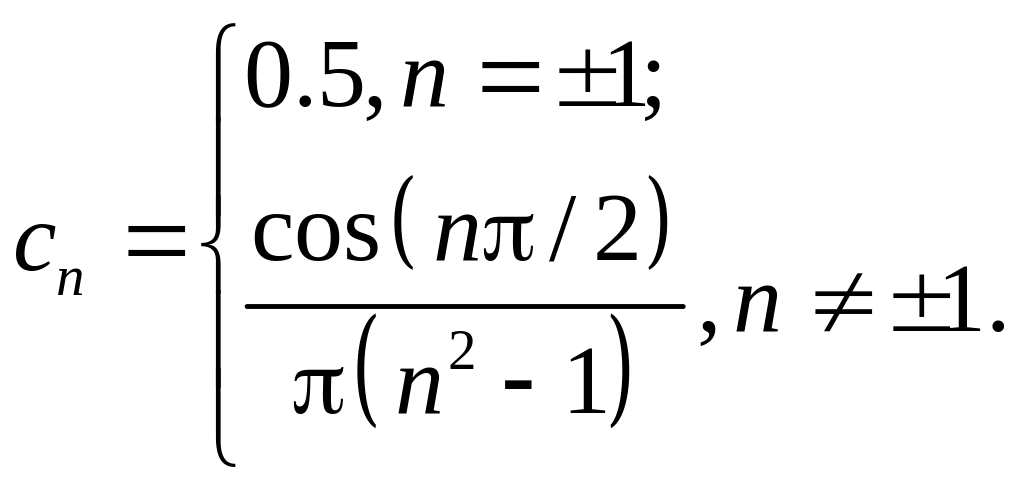
Використати розв’язок 3 і 4 задач.
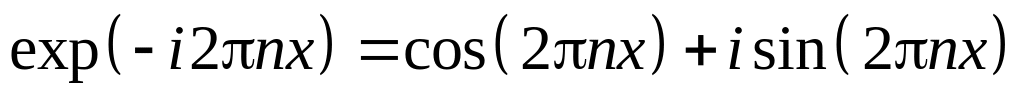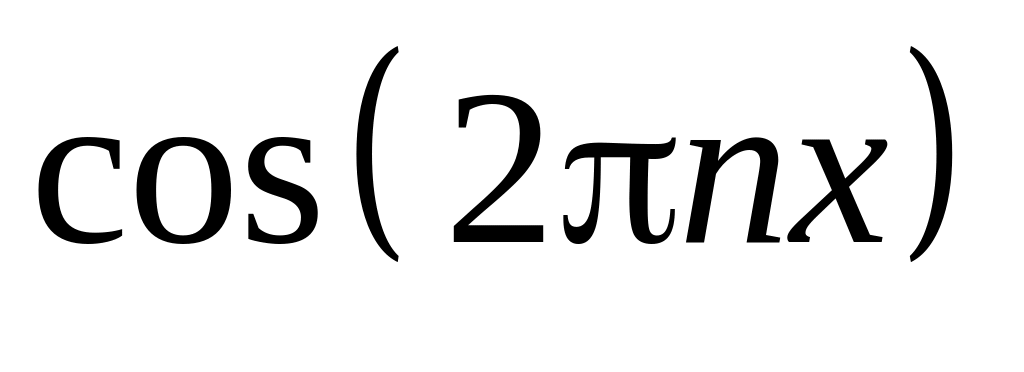Записати і використати симетричність функції і анти симетричність .
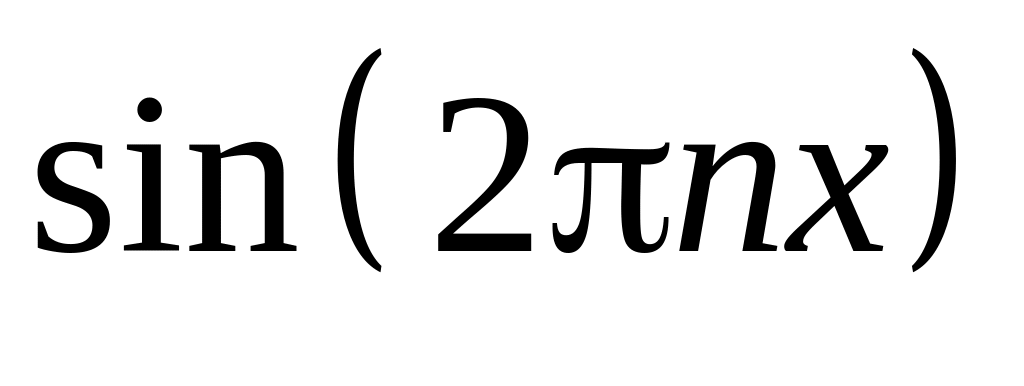Записати і використати симетричність функції і анти симетричність .
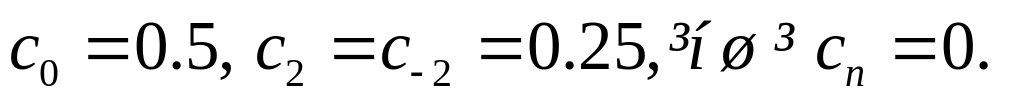
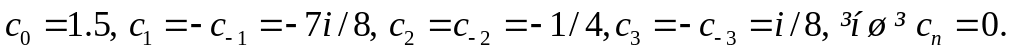
Вказівка: знайти коефіцієнти ряду Фур’є як граничний випадок від періодичної послідовності прямокутних імпульсів тривалістю і амплітудою коли
Вказівка: у виразі 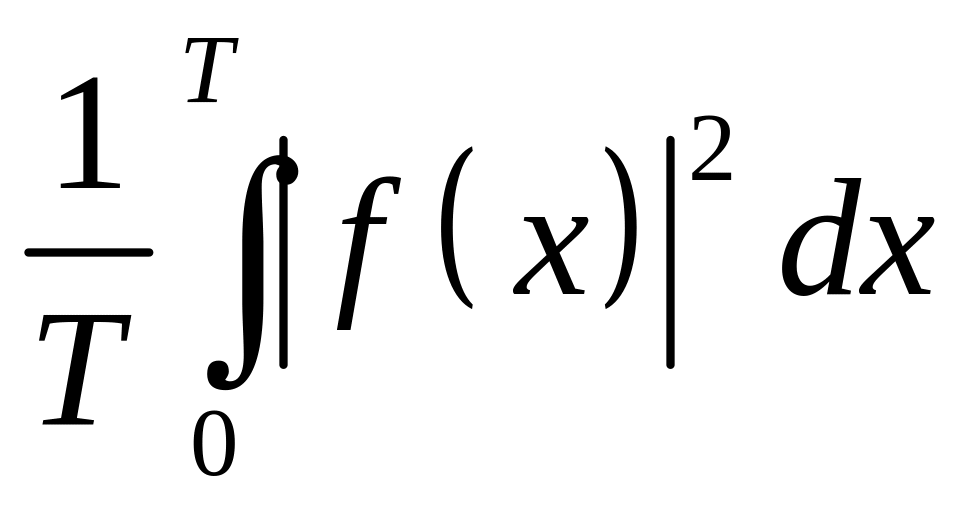функцію представити у вигляді розкладу в ряд Фур’є і скористатись ортогональністю функцій
Вказівка: Використати ортогональність функцій
Вказівка: Використати ортогональність функцій
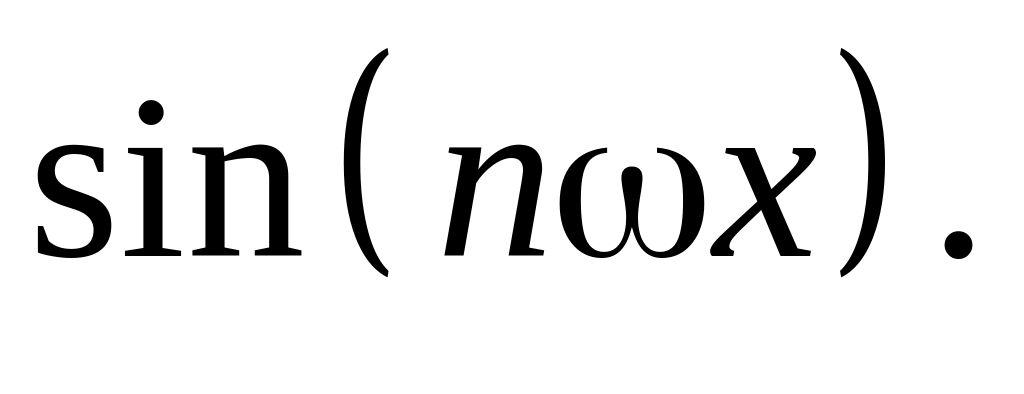
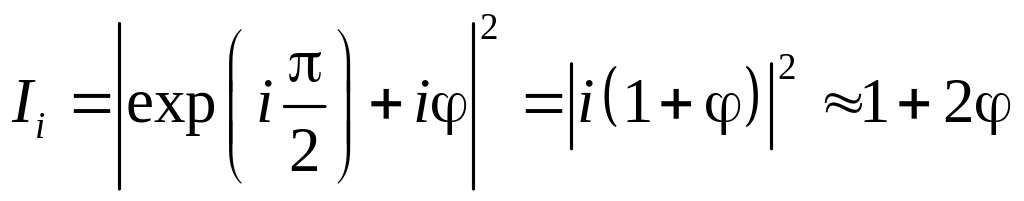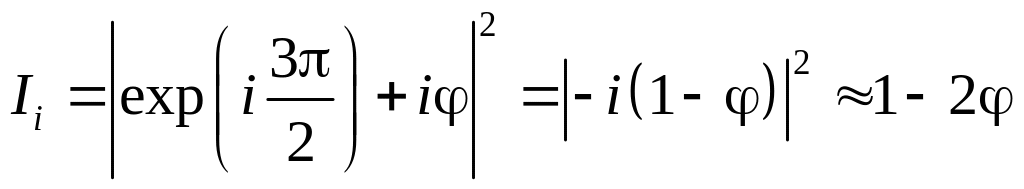