
- •Періодичні функції і розклад їх в ряд фур’є
- •Показати, що для періодичної функції для якої ,
- •Знайти коефіцієнти розкладу функції з періодом якщо
- •Знайти коефіцієнти розкладу функції з періодом якщо
- •Перетворення Фур’є та його властивості
- •Теорема про відліки
- •Дискретне перетворення Фур’є
- •Перетворення Адамара
- •Лінійні системи
- •Задачі на поширення світла та його дифракцію Плоскі та сферичні хвилі
- •Інтеграл Френеля-Кірхгофа
- •Дифракційні формули Френеля і Фраунгофера
- •Сферична лінза та її властивості
- •Частотний аналіз оптичних систем
- •Просторова фільтрація
- •Розширення та фільтрація лазерного пучка
- •Методи візуалізації фазових неоднорідностей
- •Метод фазового контрасту
- •Відповіді та вказівки до розв’язку задач з топоСу Періодичні функції і розклад їх в ряд Фур’є
- •Перетворення фур’є та інші перетворення
- •Поширення світла та його дифракція
- •Частотний аналіз оптичних систем
- •Просторова фільтрація
Лінійні системи
Під системою потрібно розуміти все те, що здійснює перетворення ряду вхідних функцій в ряд вихідних функцій. В електричних схемах вхідні і вихідні сигнали представляють собою дійсні функції (напруга чи струм) одної незалежної змінної (часу), тоді як в системах, що створюють зображення, вхідні і вихідні сигнали можуть бути дійсними (інтенсивність) або комплексними (амплітуда поля) функціями двох незалежних змінних (просторових координат).
Вхідний
![]() і вихідний
і вихідний
![]() сигнали
лінійної системи можна зв’язати простим
співвідношенням:
сигнали
лінійної системи можна зв’язати простим
співвідношенням:
|
де![]() називається імпульсним відгуком системи,
тобто відгуком на вхідний сигнал у
вигляді дельта-функції.
називається імпульсним відгуком системи,
тобто відгуком на вхідний сигнал у
вигляді дельта-функції.
Лінійна
оптична система просторово
інваріантна (або, по
іншому, ізопланарна),
коли її імпульсний відгук
![]() залежить тільки від
відстаней
залежить тільки від
відстаней
![]() і
і
![]() Для таких систем можна, очевидно, написати
Для таких систем можна, очевидно, написати
|
Для таких систем вихідний сигнал зв’язаний з вхідним сигналом з допомогою згортки:
|
Якщо взяти перетворення Фур’є правої і лівої частини, врахувавши теорему про згортку, отримаємо:
|
де
![]() — фур’є-образ імпульсного відгуку
— фур’є-образ імпульсного відгуку
|
Функція називається передавальною функцією системи, показує як діє система в “частотній області”.
ЗАДАЧІ
Доказати, що коли , то
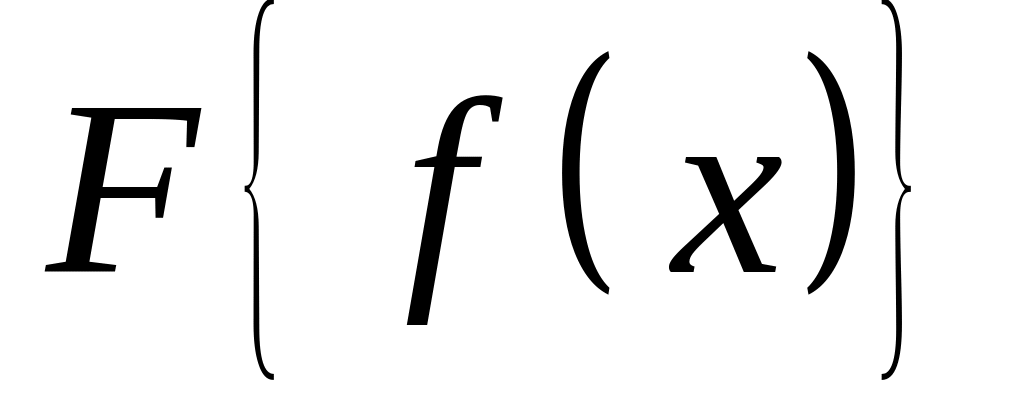 — дійсна функція.
— дійсна функція.Доказати, що коли , то — уявна функція.
Якщо для абсолютно інтегрованої функції
 то
то
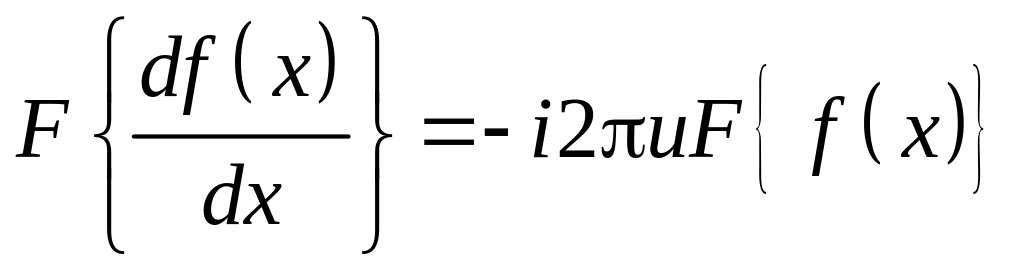 .
.Якщо для абсолютно інтегрованої функції
 і
і
 то
то

Довести, що
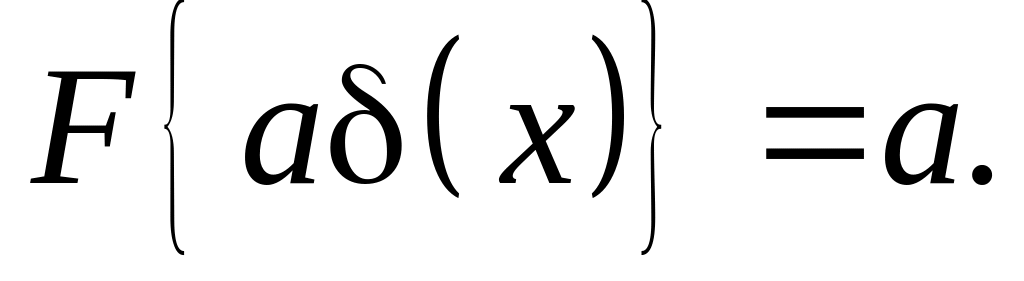
Довести, що

Довести, що

Довести, що
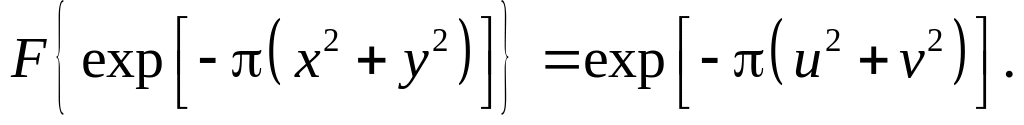
Довести, що
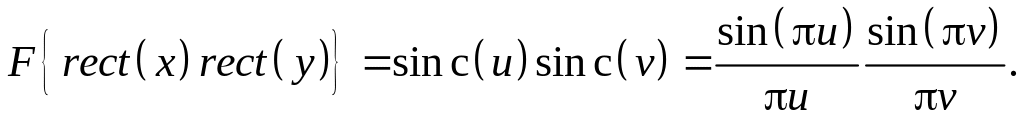
Довести, що
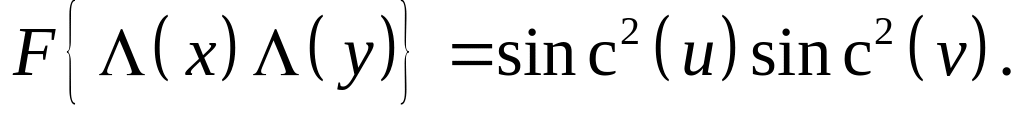 Вказівка:
скористатись теоремою про автокореляцію.
Вказівка:
скористатись теоремою про автокореляцію.Довести, що
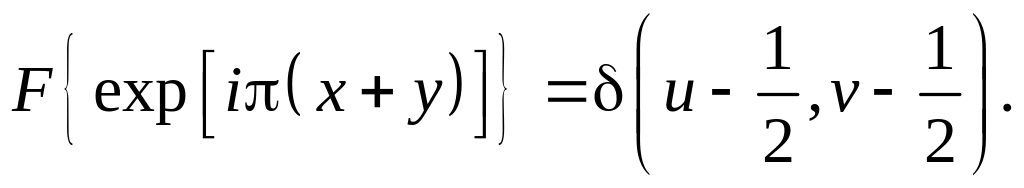 Вказівка: скористатись
теоремою про зміщення
Вказівка: скористатись
теоремою про зміщенняДовести що
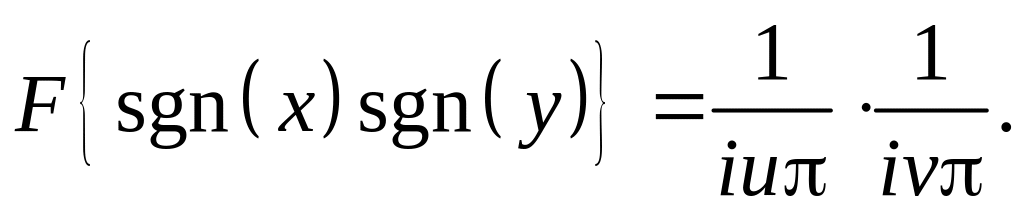 Вказівка:
Знайти перетворення Фур’є від такої
функції:
Вказівка:
Знайти перетворення Фур’є від такої
функції: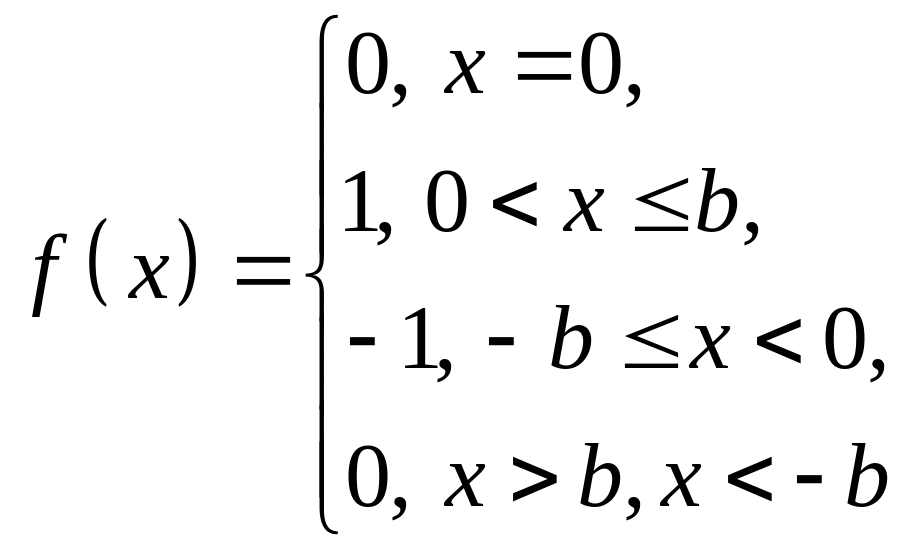 і
границю отриманого результату при
і
границю отриманого результату при

Довести що
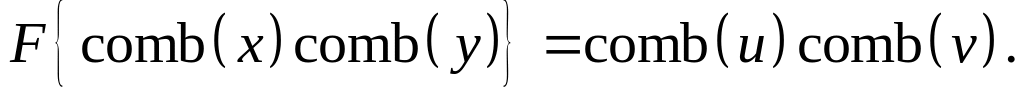
Знайти фур’є-образ функції
 прямим методом і з використанням теорем
про зміщення та подібності.
прямим методом і з використанням теорем
про зміщення та подібності.Знайти фур’є-спектр такої функції:
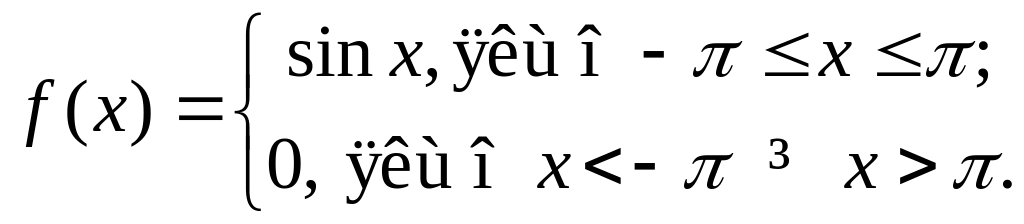
Знайти фур’є-спектр такої функції:

Знайти фур’є-спектр такої функції:
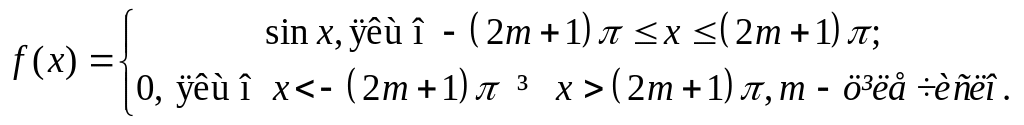
Знайти фур’є-спектр такої функції:

Знайти фур’є-спектр такої функції:
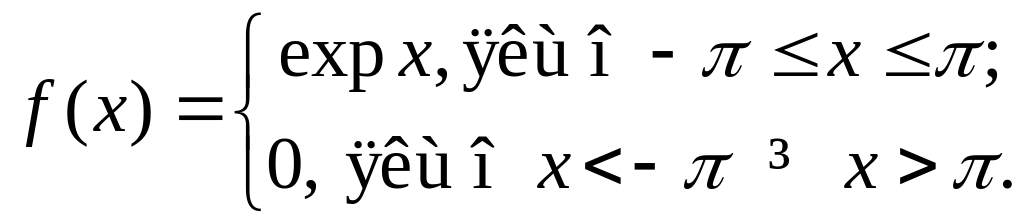
Знайти фур’є-спектр функції
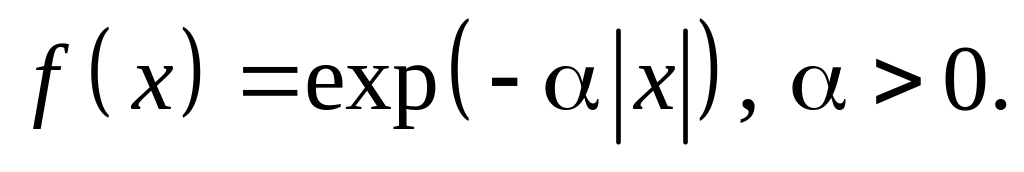
Знайти фур’є-спектр функції
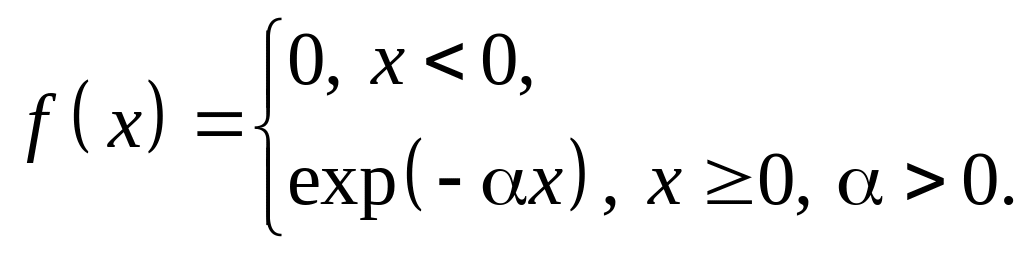
Знайти фур’є-спектр функції
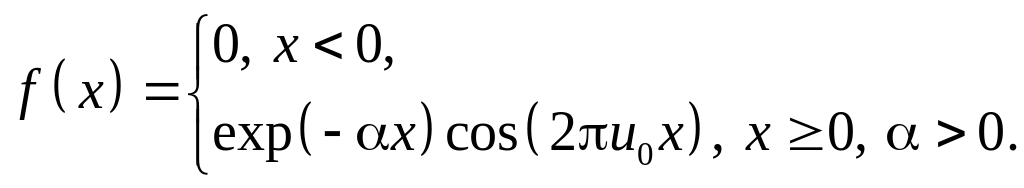
Знайти фур’є-спектр функції

Знайти фур’є-спектр функції

Знайти фур’є-спектр функції
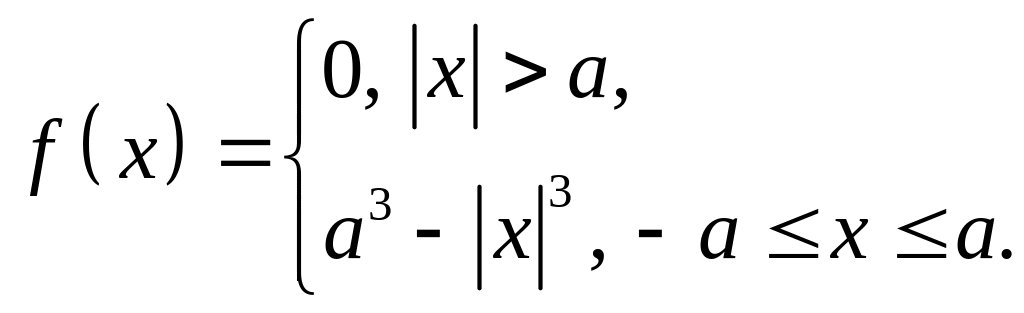
Знайти фур’є-спектр функції
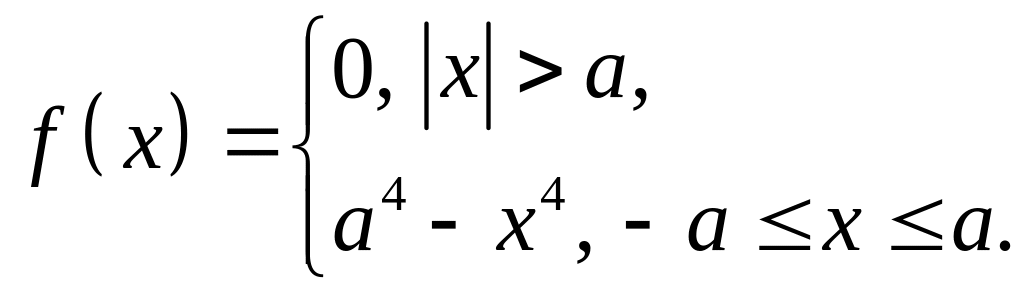
Методом перетворення Фур’є знайти постійні поширення хвилеводних мод планарного симетричного хвилеводу, а також поле трьох найнижчих мод для довжини хвилі 0.6328 мкм. Визначити число локалізованих мод, що поширюються в хвилеводі. Діелектрична стала описується такими функціями:

1.
![]()
![]()
![]()
![]() .
.
2.
![]()
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() ,
,
![]() .
.
6.
![]() ,
.
,
.
28. „Еквівалентну площу”
![]() функції
функції
![]() можна визначити так:
можна визначити так:
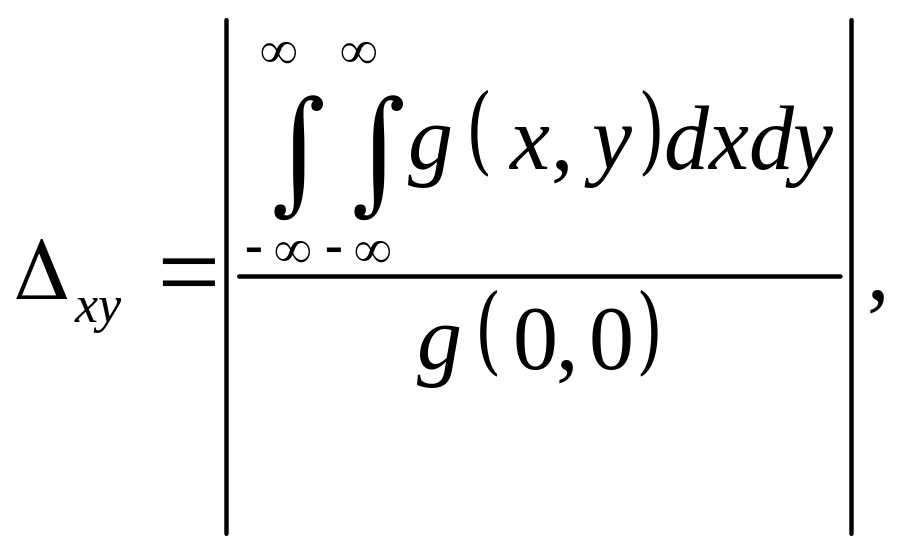
одночасно „еквівалентна
ширина спектру” функції
![]() зв’язана з її образом наступним виразом:
зв’язана з її образом наступним виразом:

Показати, що
![]()
29.Знайти максимальний інтервал
![]() відліку функції
відліку функції
![]() ,
якщо
,
якщо
![]()
30.Знайти максимальний інтервал
![]() функції
функції
![]()
31. Знайти максимальний інтервал
функції
![]()
32. Провести оцінку максимального
інтервалу
відліку функції
![]() – функція Гауса.
– функція Гауса.
33. Знайти похибку між значеннями
![]() та її представленням згідно теореми
про відліки, та провести дослідження
величини похибки від
.
та її представленням згідно теореми
про відліки, та провести дослідження
величини похибки від
.
34. Провести оцінку максимального
інтервалу
відліку функції
![]()
35. Знайти похибку між значеннями
![]() та її представленням згідно теореми
про відліки, та провести дослідження
величини похибки від
.
та її представленням згідно теореми
про відліки, та провести дослідження
величини похибки від
.
36. Довести, що рядки і стовпці матриці дискретного фур’є-перетворення є ортогональні.
37. Довести, що сума елементів кожного рядка (стовпця), за виключенням першого, матриці дискретного фур’є-перетворення рівна нулю.
38. Довести, що рядки і стовпці матриці Адамара є ортогональні.
39. Довести, що сума елементів кожного рядка (стовпця), за виключенням першого, матриці Адамара рівна нулю.
40. Довести теорему Парсеваля для перетворення Адамара.
41. Знайти
перетворення Адамара матриці
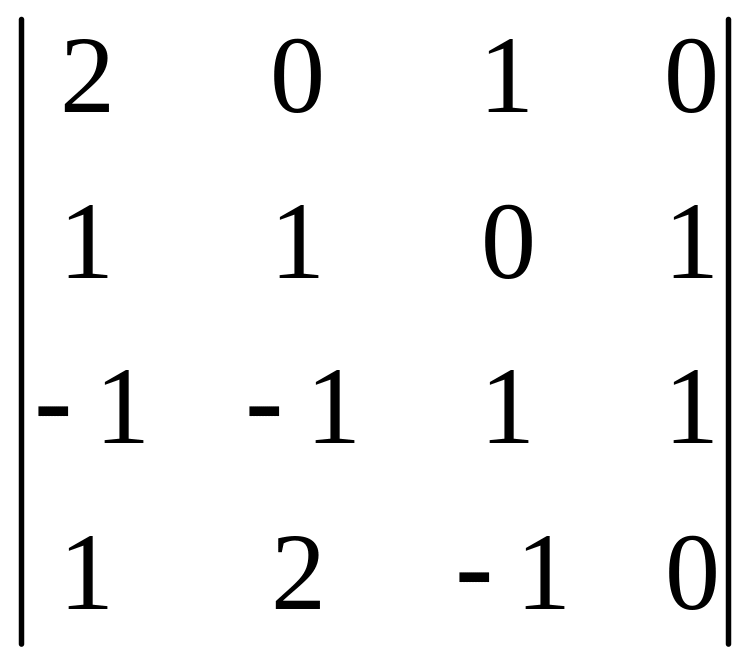 ,
провести перевірку теореми Парсеваля.
,
провести перевірку теореми Парсеваля.
42. Знайти
перетворення Адамара матриці
 ,
провести перевірку теореми Парсеваля.
,
провести перевірку теореми Парсеваля.
43. Знайти перетворення Адамара
матриці
 ,
провести перевірку теореми Парсеваля.
,
провести перевірку теореми Парсеваля.
44. Знайти перетворення Адамара
матриці
 ,
провести перевірку теореми Парсеваля.
,
провести перевірку теореми Парсеваля.
45. Знайти
![]() ,
якщо
,
якщо
 ,
а
,
а
![]() .
.
46.Знайти перетворення Фур'є
від функції
![]()
47. Знайти перетворення Фур'є
від функції
![]() ,
,
48. Знайти перетворення Фур'є від функції
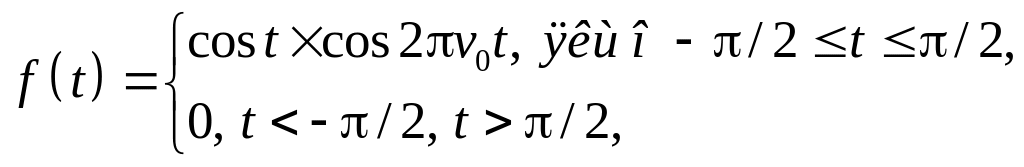
![]()
49. Знайти перетворення Фур'є
від функції
![]()
![]()
50. Знайти перетворення Фур'є
від функції

