
- •Періодичні функції і розклад їх в ряд фур’є
- •Показати, що для періодичної функції для якої ,
- •Знайти коефіцієнти розкладу функції з періодом якщо
- •Знайти коефіцієнти розкладу функції з періодом якщо
- •Перетворення Фур’є та його властивості
- •Теорема про відліки
- •Дискретне перетворення Фур’є
- •Перетворення Адамара
- •Лінійні системи
- •Задачі на поширення світла та його дифракцію Плоскі та сферичні хвилі
- •Інтеграл Френеля-Кірхгофа
- •Дифракційні формули Френеля і Фраунгофера
- •Сферична лінза та її властивості
- •Частотний аналіз оптичних систем
- •Просторова фільтрація
- •Розширення та фільтрація лазерного пучка
- •Методи візуалізації фазових неоднорідностей
- •Метод фазового контрасту
- •Відповіді та вказівки до розв’язку задач з топоСу Періодичні функції і розклад їх в ряд Фур’є
- •Перетворення фур’є та інші перетворення
- •Поширення світла та його дифракція
- •Частотний аналіз оптичних систем
- •Просторова фільтрація
Періодичні функції і розклад їх в ряд фур’є
Функція
![]() називається періодичною, якщо існує
таке найменше позитивне число
називається періодичною, якщо існує
таке найменше позитивне число
![]() ,
що для всіх
,
що для всіх
![]() з області визначення функції
справедливе співвідношення:
з області визначення функції
справедливе співвідношення:
![]() .
.
Нехай дано періодичну функцію з періодом . Її можна розкласти в ряд Фур’є наступним чином:
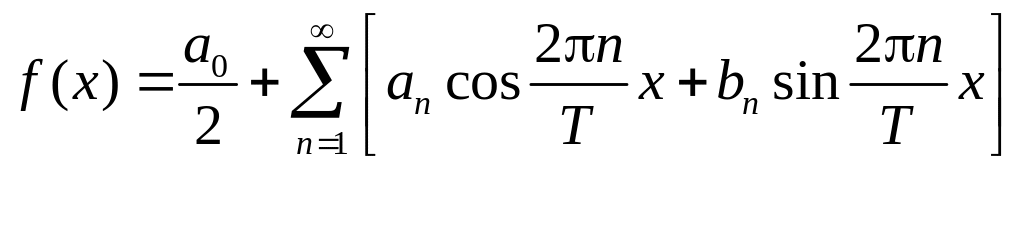 .
.
де:
![]() ,
,
![]() ,
,
![]()
![]() — циклічна частота. Отже
розклад
в ряд Фур’є можна представити наступним
чином:
— циклічна частота. Отже
розклад
в ряд Фур’є можна представити наступним
чином:
![]()
Як відомо:
![]() .
.
![]()
Перегрупуємо члени в квадратних дужках, отримаємо:
![]() ,
,
де:
![]()
![]() Коефіцієнти розкладу періодичної
функції в комплексний ряд Фур’є можна
найти ще наступним чином:
Коефіцієнти розкладу періодичної
функції в комплексний ряд Фур’є можна
найти ще наступним чином:
![]() .
.
Для періодичних функцій справедливе співвідношення:
![]() — теорема Парсеваля.
— теорема Парсеваля.
ЗАДАЧІ
Знайти коефіцієнти розкладу
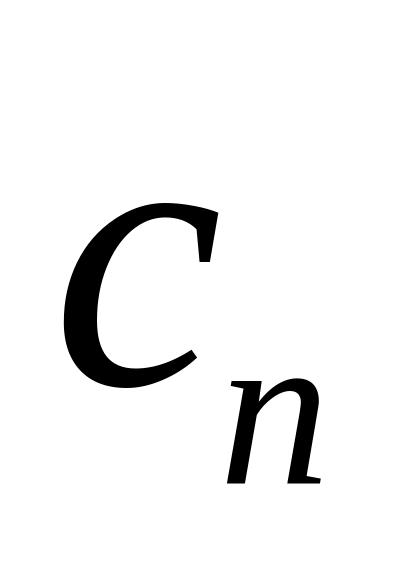 функції
з періодом
функції
з періодом
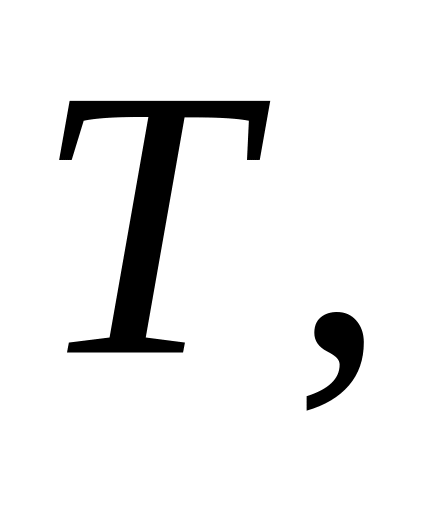 якщо
якщо
 Перевірити теорему Парсеваля.
Перевірити теорему Парсеваля.Знайти коефіцієнти розкладу функції з періодом якщо
 на інтервалі
на інтервалі
 і дальше періодично продовжена.
і дальше періодично продовжена.Знайти коефіцієнти розкладу функції
 з періодом
якщо
з періодом
якщо
 коли
коли
 ,
, ,
коли
,
коли
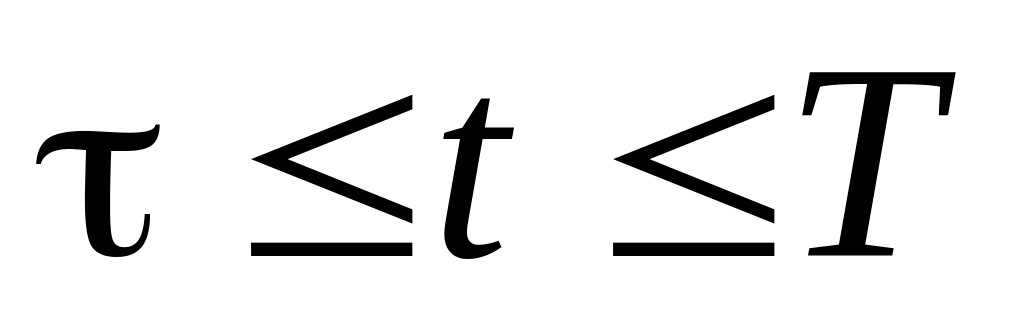 .
.
Знайти коефіцієнти розкладу функції з періодом якщо
 ,
коли
,
,
коли
,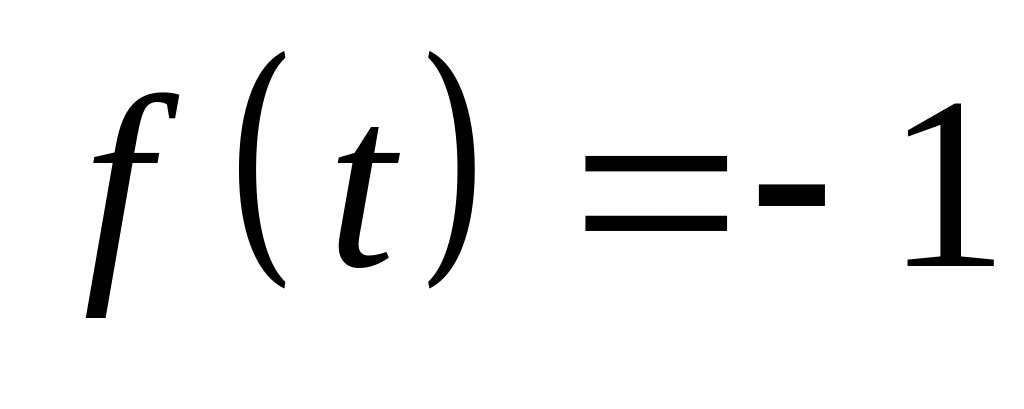 ,
коли
.
При якому значенні
,
коли
.
При якому значенні

 — мінімальне, а
— мінімальне, а
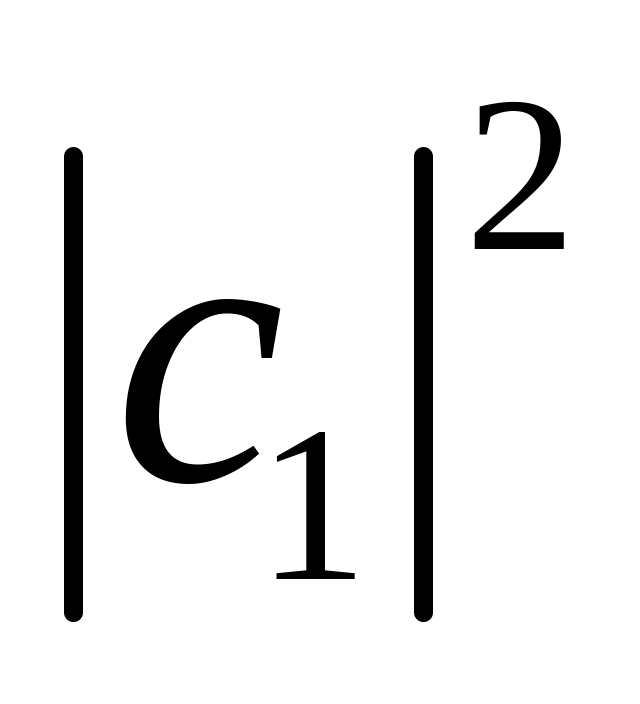 — максимальне.
— максимальне.Знайти коефіцієнти розкладу функції з періодом якщо
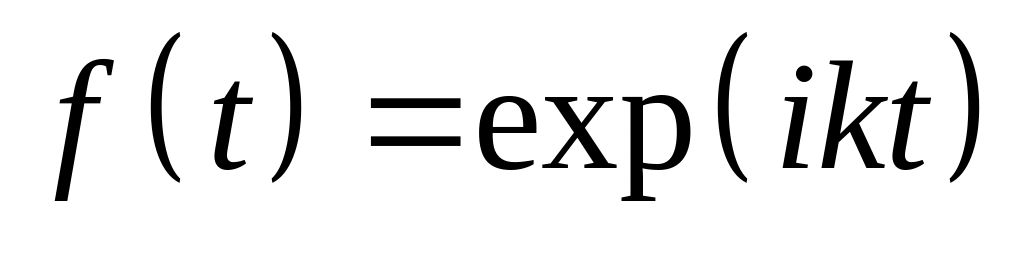 на інтервалі
і дальше періодично продовжена. Знайдіть
на інтервалі
і дальше періодично продовжена. Знайдіть
 при якому комплексний ряд Фур’є цієї
функції містить тільки один член
розкладу.
при якому комплексний ряд Фур’є цієї
функції містить тільки один член
розкладу.Знайти коефіцієнти розкладу функції з періодом якщо
 (двох
півперіодний випростовувач).
(двох
півперіодний випростовувач).Знайти коефіцієнти розкладу функції з періодом якщо
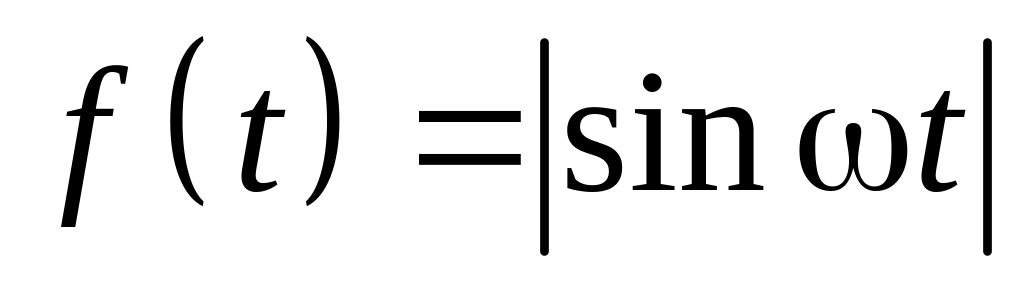 .
.Розкласти в ряд Фур’є функцію
 (півперіодний випростовувач).
(півперіодний випростовувач).Розкласти в ряд Фур’є функцію
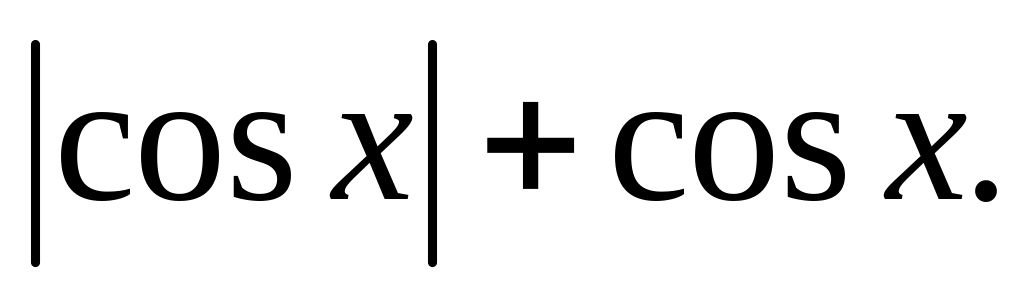
Знайти коефіцієнти розкладу функції з періодом якщо
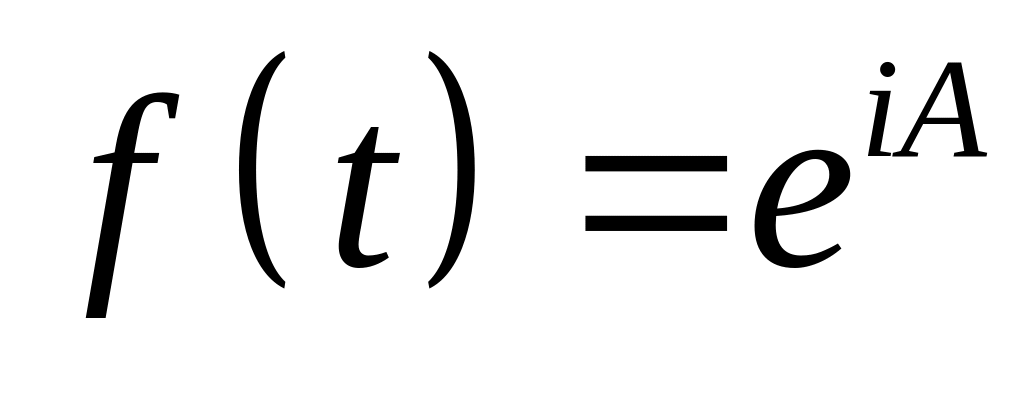 ,
коли
,
,
коли
.
При яких значеннях
А і
— мінімальне, а
— максимальне.
,
коли
,
,
коли
.
При яких значеннях
А і
— мінімальне, а
— максимальне.
Показати, що для періодичної функції для якої
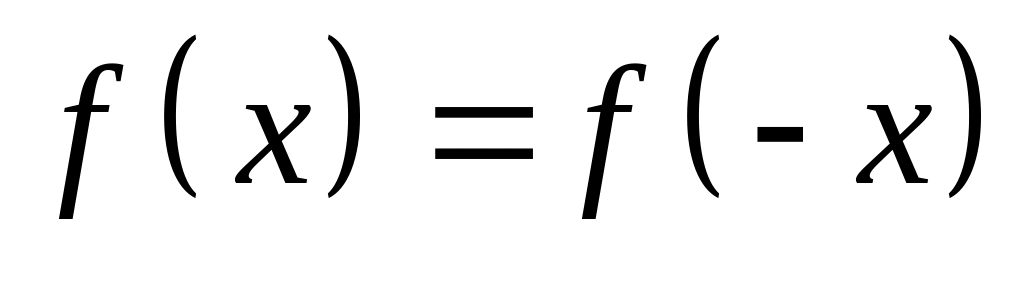 ,
,

Показати, що для періодичної функції для якої ,
Знайти коефіцієнти розкладу функції з періодом якщо
Знайти коефіцієнти розкладу функції з періодом якщо
Розкласти в комплексний ряд Фур’є функцію 1+

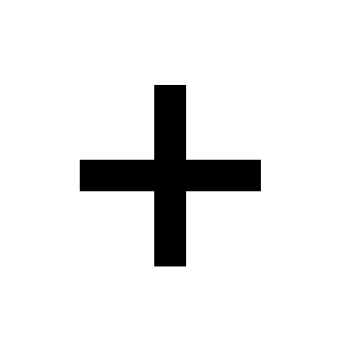
 .
.Розкласти в комплексний ряд Фур’є функцію 1+

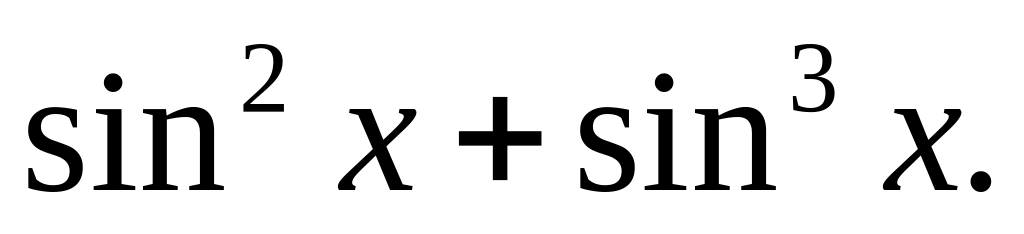 .
.Знайти коефіцієнти розкладу функції з періодом , якщо
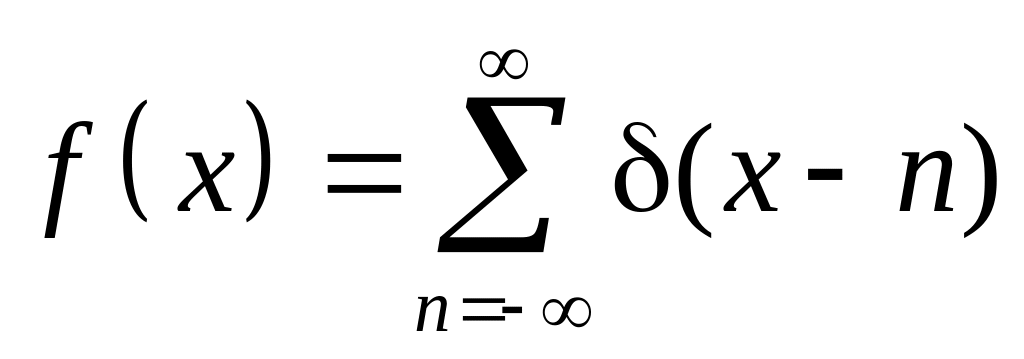 .
Ця функція представляє собою гребінку
дельта-функцій і має спеціальну назву
.
Ця функція представляє собою гребінку
дельта-функцій і має спеціальну назву
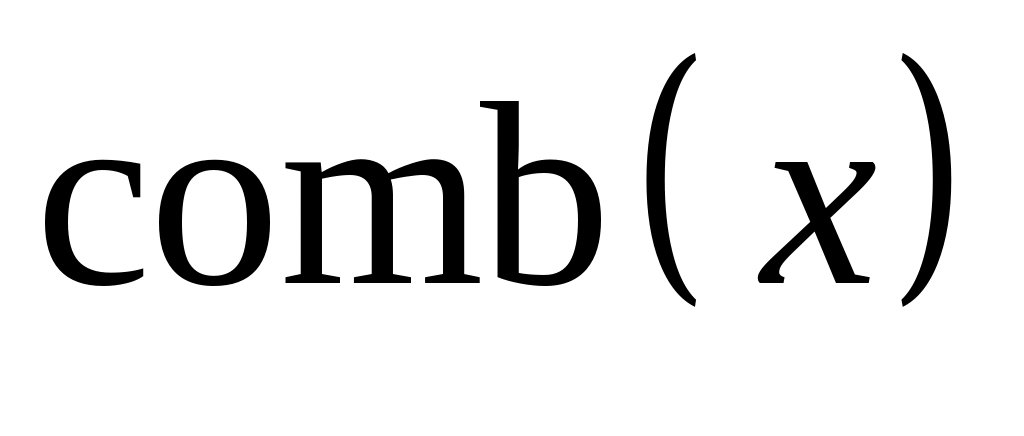 .
.Довести теорему Парсеваля для дійсних періодичних симетричних функцій.
Довести теорему Парсеваля для дійсних періодичних антисиметричних функцій.
Довести теорему Парсеваля для періодичних функцій.
ПЕРЕТВОРЕННЯ ФУР’Є ТА ІНШІ ОРТОГОНАЛЬНІ ПЕРЕТВОРЕННЯ
Перетворення Фур’є та його властивості
Перетворення Фур’є, або
фур’є-образ (по іншому спектр Фур’є,
або частотний спектр) комплексної
функції
![]() двох незалежних змінних x
та y,
яке будемо позначати
двох незалежних змінних x
та y,
яке будемо позначати
![]() ,
визначається:
,
визначається:
![]() .
.
Це співвідношення можна
написати в операторній формі
![]()
Таким же чином вводиться
обернене перетворення, з допомогою
якого по
можна знайти функцію
![]()
![]() .
.
Перетворення Фур’є існує,
якщо функція
абсолютно інтегрована по нескінченній
площині
![]() ,
тобто:
,
тобто:
![]() <
M – скінчене число.
<
M – скінчене число.
Для функцій, які, строго кажучи, не задовольняють умовам існування, часто можна знайти перетворення, якщо ці функції вдається визначити як границю послідовності функцій, що піддаються перетворенню Фур’є. Перетворюючи кожен член послідовності, ми отримуємо відповідну послідовність фур’є-образів, границю якої називають узагальненим фур’є-образом вихідної функції.
