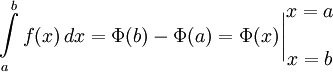Определённый интеграл
Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).
Определение
Пусть
![]() определена
на
определена
на
![]() .
Разобьём
на
части с несколькими произвольными
точками
.
Разобьём
на
части с несколькими произвольными
точками
![]() .
Тогда говорят, что произведено разбиение
.
Тогда говорят, что произведено разбиение
![]() отрезка
отрезка
![]() Далее
выберем произвольную точку
Далее
выберем произвольную точку
![]() ,
,
![]() ,
,
Определённым
интегралом от функции
на
отрезке
называется
предел интегральных сумм при стремлении
ранга разбиения к нулю
![]() ,
если он существует независимо от
разбиения
и
выбора точек
,
если он существует независимо от
разбиения
и
выбора точек
![]() ,
то есть
,
то есть
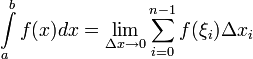
Если существует указанный предел, то функция называется интегрируемой на по Риману.
Обозначения
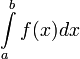
 —
нижний
предел.
—
нижний
предел.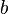 —
верхний
предел.
—
верхний
предел.— подынтегральная функция.
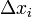 —
длина
частичного отрезка.
—
длина
частичного отрезка.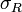 —
интегральная
сумма от функции
на
соответствующей
разбиению
.
—
интегральная
сумма от функции
на
соответствующей
разбиению
.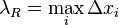 —
максимальная
длина част. отрезка.
—
максимальная
длина част. отрезка.
Свойства
Если функция интегрируема по Риману на , то она ограничена на нем.
Геометрический смысл
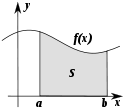
Определённый интеграл как площадь фигуры
Определённый
интеграл
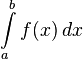 численно
равен площади фигуры, ограниченной осью
абсцисс, прямыми
численно
равен площади фигуры, ограниченной осью
абсцисс, прямыми
![]() и
и
![]() и
графиком функции
.
и
графиком функции
.
Теорема Ньютона — Лейбница
'Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определённого интеграла и вычислением первообразной.
-
Если
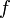 непрерывна
на отрезке
непрерывна
на отрезке
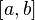 и
и
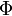 —
её любая первообразная на этом
отрезке, то имеет место равенство
—
её любая первообразная на этом
отрезке, то имеет место равенство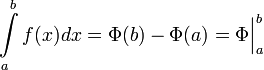
Доказательство
Пусть на отрезке задана интегрируемая функция . Начнём с того, что отметим, что
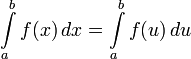
то
есть не имеет никакого значения, какая
буква (![]() или
или
![]() )
стоит под знаком
в
определённом интеграле по отрезку
.
)
стоит под знаком
в
определённом интеграле по отрезку
.
Зададим
произвольное значение
![]() и
определим новую функцию
и
определим новую функцию
![]() .
Она определена для всех значений
,
потому что мы знаем, что если существует
интеграл от
на
,
то существует также интеграл от
на
.
Она определена для всех значений
,
потому что мы знаем, что если существует
интеграл от
на
,
то существует также интеграл от
на
![]() ,
где
,
где
![]() .
Напомним, что мы считаем по определению
.
Напомним, что мы считаем по определению
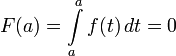 (1)
(1)
Заметим, что
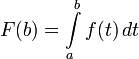
Покажем,
что
![]() непрерывна
на отрезке
.
В самом деле, пусть
непрерывна
на отрезке
.
В самом деле, пусть
![]() ;
тогда
;
тогда
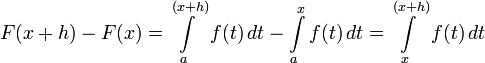
и
если
![]() ,
то
,
то
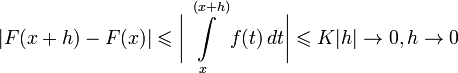
Таким образом, непрерывна на независимо от того, имеет или не имеет разрывы; важно, что интегрируема на .

На
рисунке изображён график
.
Площадь переменной фигуры
![]() равна
равна
![]() .
Её приращение
.
Её приращение
![]() равно
площади фигуры
равно
площади фигуры
![]() ,
которая в силу ограниченности
,
очевидно, стремится к нулю при
,
которая в силу ограниченности
,
очевидно, стремится к нулю при
![]() независимо
от того, будет ли
точкой
непрерывности или разрыва
,
например точкой
независимо
от того, будет ли
точкой
непрерывности или разрыва
,
например точкой
![]() .
.
Пусть
теперь функция
не
только интегрируема на
,
но непрерывна в точке
![]() .
Докажем, что тогда
имеет
в этой точке производную, равную
.
Докажем, что тогда
имеет
в этой точке производную, равную
![]() (2)
(2)
В самом деле, для указанной точки
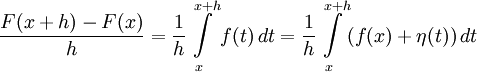
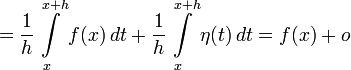 (1)
,
(3)
(1)
,
(3)
Мы
положили
![]() ,
а так как
,
а так как
![]() постоянная
относительно
постоянная
относительно
![]() ,
то
,
то
![]() .
Далее, в силу непрерывности
в
точке
для
всякого
.
Далее, в силу непрерывности
в
точке
для
всякого
![]() можно
указать такое
можно
указать такое
![]() ,
что
,
что
![]() для
для
![]() .
.
Поэтому

что
доказывает, что левая часть этого
неравенства есть о(1) при
![]() .
.
Переход
к пределу в (3) при
показывает
существование производной от
в
точке
и
справедливость равенства (2). При
![]() речь
здесь идёт соответственно о правой и
левой производной.
речь
здесь идёт соответственно о правой и
левой производной.
Если функция непрерывна на , то на основании доказанного выше соответствующая ей функция
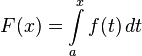 (4)
(4)
имеет
производную, равную
![]() .
Следовательно, функция
есть
первообразная для
на
.
.
Следовательно, функция
есть
первообразная для
на
.
Это заключение иногда называется теоремой об интеграле с переменным верхним пределом или теоремой Барроу.
Мы доказали, что произвольная непрерывная на отрезке функция имеет на этом отрезке первообразную, определенную равенством (4). Этим доказано существование первообразной для всякой непрерывной на отрезке функции.
Пусть
теперь
есть
произвольная первообразная функции
на
.
Мы знаем, что
![]() ,
где
,
где
![]() —
некоторая постоянная. Полагая в этом
равенстве
—
некоторая постоянная. Полагая в этом
равенстве
![]() и
учитывая, что
и
учитывая, что
![]() ,
получим
,
получим
![]() .
.
Таким
образом,
![]() .
Но
.
Но
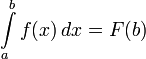
Поэтому