5. Распределение случайной величины

Для того чтобы исследовать закономерности, связанные со случайным характером факторов риска и показателей здоровья, необходима информация о том, какова вероятность появления различных значений этих величин в испытаниях (например, вероятность различных степеней ожога при пожаре или вероятность различных величин прироста артериального давления под действием эмоционального стресса). Эта информация для случайной величины ξ задается с помощью функции распределения F (эквивалентные термины — функция распределения вероятностей и кумулятивная функция распределения). Функция рас­пределения F(х) для любого значения х равна вероятности того, что случайная величина ξ не превосходит х (ξ ≤ х):

F(x) = P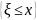

Из этого определения следуют основные свойства функции распределения:

1. F(х) — неубывающая функция;

2. Все значения F(х) лежат в интервале от 0 до 1:

0 ≤ F(x) ≤ 1;

3. Когда х неограниченно убывает (стремится к минус бесконечности), F(х) стремится к 0:

X - 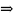F(x) 0;

4. Когда х неограниченно возрастает (стремится к бесконечности), F(х) стремится к 1:

X F(x) 1.

Дискретные случайные величины

Факторы риска и показатели здоровья подразделяются на 2 класса — дискретных и непрерывных случайных величин, — в зависимости от того, каково множество допустимых значений этих величин.

Случайная величина ξ называется дискретной, если она принимает конечное или счетное число различных значений. Между любыми двумя течениями дискретной величины может находиться лишь конечное число ее значений. Примерами дискретных величин являются:

- число случаев заболевания в определенной группе населения за 1 год;

- возраст в полных годах;

- степень тяжести заболеваний и повреждений.

Распределение дискретной случайной величины ξ полностью определено, если для каждого ее значения х_i указана вероятность его появления (обозначаемая как р_i): р_i = P Функция, устанавливающая взаимосвязь между значениями х_i и р_i, называется законом распределения или вероятностной функцией дискретной случайной величины. Эта функция может быть задана различными способами: в виде табли­цы, графика или аналитической зависимости. Например, табличный способ задания закона распределения дискретной случайной величины имеет следующий вид:

ξ :

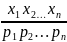
Сумма вероятностей р_i, по всем значениям индекса i равна 1, и для любого значения х значение функции распределения F(х) равно сумме вероятностей р_i по всем x_i ≤ х. Таким образом, F(х) есть ступенчатая функция, сохраняющая постоянное значение на любом интервале, не содержащем точек х_i, а в каждой точке x_i имеющая скачок на величину р_i.

При оценке рисков наиболее часто приходится иметь дело со следующими видами распределения дискретных случайных величин:

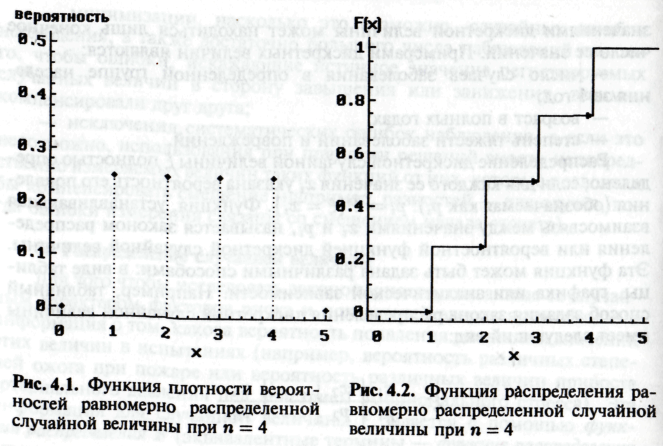
Дискретное равномерное распределение. Для случайных величин, распределенных по дискретному равномерному закону, каждое из п возможных значений x₁,..., х_n принимается с вероятностью 1/n (р_i, = 1/n для любого i). Такие случайные величины используются в качестве модели событий с равновероятными исходами. Так например, если организация технологического процесса такова, что персонал подразделяется на 4 равных по численности группы в зависимости от характера контакта с агентом риска:

1. — контакт с агентом риска исключен;

2. — эпизодические непродолжительные контакты;

3. — систематические непродолжительные контакты;

4. — постоянный контакт с агентом риска в течение всего рабочего времени, то распределение персонала по уровням данного фактора риска является равномерным (рис. 4.1, 4.2).

Распределение Бернулли описывает случайные величины, принимающие два значения — 0 и 1 — с вероятностями, соответственно, q = 1 - р и р. Показатель р называется параметром распределения. Случайные величины, распределенные по закону Бернулли, служат моделью событий с двумя возможными исходами (например, наличие или отсутствие заболевания). Распределение Бернулли может быть использовано для описания индивидуального риска (например, если величина р равна вероятности смерти от рака в результате воздействия канцерогена, то она является характеристикой канцерогенного риска).

При р = q = 1/2 распределение Бернулли является частным случаем равномерного.

Распределение Пуассона (рис. 4.3, 4.4). Случайная величина, принимающая счетное множество значений 0, 1, 2, ... (любое неотрицатель­ное целое число) с вероятностями.

₌

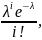
где функция і! (факториал целого числа і) определяется следующим образом:

= 1, а для любого = ( )

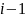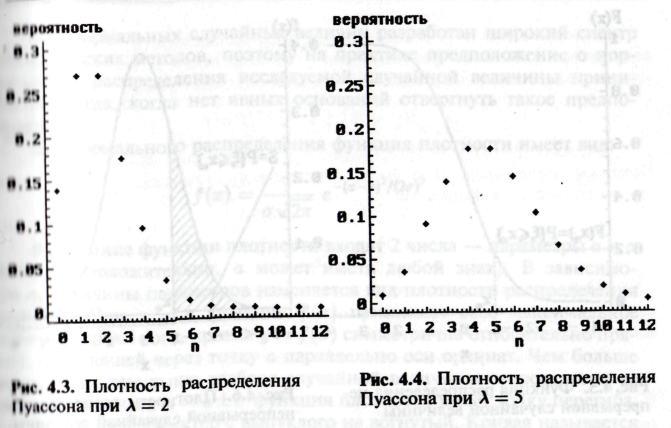
Величина λ называется параметром распределения Пуассона. Распределение Пуассона является хорошей моделью для оценки риска отдельных взаимно независимых эффектов фактора риска, например, вероятности определенного числа травм в расчете на 1 человеко-год на травмоопасном производстве. Рис. 4.3 и 4.4 иллюстрируют такую ситуацию для различных значений параметра λ: при λ = 2 наиболее вероятны 1 или 2 случая травм на 1 человеко-год, при λ = 5 – 4 или 5 случаев.

Непрерывные случайные величины

Непрерывными называются величины, которые могут принимать любое значение на некотором интервале. Между любыми двумя значениями непрерывной величины содержится бесконечное число ее значений. К непрерывным относятся такие характеристики факторов риска, как концентрация, накопленная доза, и такие показатели здоровья, как заболеваемость и смертность для популяций, а также любые физиологические параметры для индивидов.

Для непрерывной случайной величины ξ функция распределении F(х) непрерывна, и, кроме того, существует непрерывная почти всюду неотрицательная функция f(х), называемая функцией плотности вероятности (а также функцией плотности или просто плотностью распределения), такая, что для любых значений х₁ < х₂ вероятность того, чю значение ξ находится в промежутке между х₁ и х₂, равна площади плоской фигуры, ограниченной сверху графиком функции у = f(х),снизу — осью абсцисс (у = 0), а слева и справа — отрезками прямых, проходящих через точки х₁ и х₂ параллельно оси ординат (х = х₁ и х = х₂ соответственно). В математическом смысле функция плотности является производной от функции распределения. Из определения вероятности ясно, что площадь, ограничиваемая графиком функции плотности и осью абсцисс, равна 1 для любого распределения.

Рис. 4.5 и 4.6 иллюстрируют возможность использования функции распределения и плотности распределения при оценке риска: если ось абсцисс соответствует уровням фактора риска, то функцию F(x) можно интерпретировать как вероятность неблагоприятного эффект фактора риска для уровня х. Для графика плотности вероятности риск, соответствующий уровню фактора х₀, соответствует площади заштрихованной фигуры.

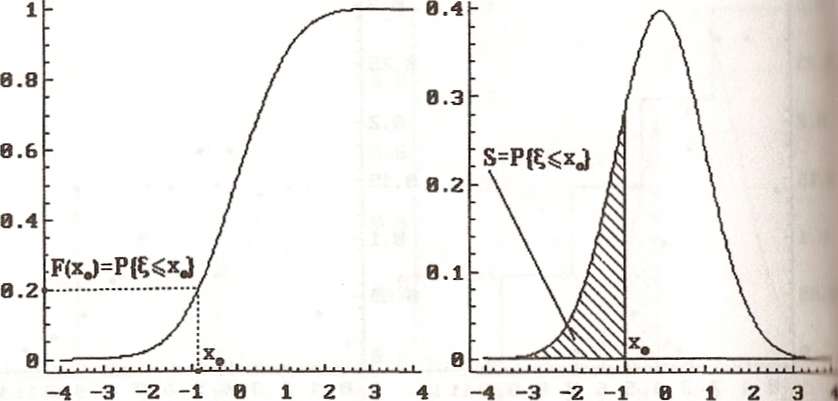
Рис. 4.5. Функция распределения Рис. 4.6. Плотность распределения непрерывной случайной величины непрерывной случайной величины

Нормальное (гауссово) распределение. Нормальное распределение играет особо важную роль как в теоретической, так и в прикладной статистике. Практическая значимость этого распределения при оценке рисков обусловлена тем, что очень многие показатели здоровья на популяционном уровне (в том числе антропологические и многие физиологические характеристики, а также показатели заболеваемости) подчиняются нормальному или приблизительно нормальному закону распределения. Кроме того, в теории вероятностей доказывается так называемая центральная предельная теорема, согласно которой нормированное распределение суммы независимых случайных величин, ни одна из которых не доминирует над остальными, сходится к нормальному распределению при увеличении числа слагаемых. Эта теорема дает, в частности, основание для того, чтобы рассматривать распределение случайных ошибок наблюдения (имеющих место при измерении как воздействий, так и характеристик здоровья) как нормальное.

Для нормальных случайных величин разработан широкий спектр статистических методов, поэтому на практике предположение о нормальности распределения исследуемой случайной величины принимается всегда, когда нет явных оснований отвергнуть такое предположение.

Для нормального распределения функция плотности имеет вид:

.

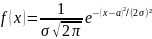В описание функции плотности входят 2 числа — параметры а и σ (σ всегда положительно, а может иметь любой знак). В зависимости от величины параметров изменяется вид плотности распределения (рис 4.7). При х = а функция f(х) принимает свое максимальное значение, кроме того, кривая у = f(х) симметрична относительно прямой, проходящей через точку а параллельно оси ординат. Чем больше величина σ, тем выше разброс случайной величины относительно ее среднего. В точках х = а ± σ функция плотности имеет точку перегиба, т. е. меняет свой характер с выпуклого на вогнутый. Кривая называется выпуклой на некотором интервале, если для любых двух точек х₁, х₂ из этого интервала отрезок прямой, соединяющий соответствующие им точки на графике f(х₁), f(х₂), (секущая) лежит ниже графика f(х),и вогнутой, если график функции для любых двух точек лежит под секущей. На практике часто используется следующее свойство нормального распределения: независимо от значений параметров а и σ площадь под графиком плотности распределения составляет:

0,68 для интервала а ± σ;

0,95 для интервала а ± 1,96 σ;

0,99 для интервала а ± 2,58σ;

0,9974 для интервала а ± 3σ.

Функция плотности нормального распределения определена для любых значений х, как положительных, так и отрицательных, причем сколь, угодно больших по абсолютной величине. В действительности же почти всегда приходится иметь дело со случайными величинами, множество значений которых ограничено и снизу, и сверху. Основанием для применения нормального распределения к реальным случайным величинам является тот факт, что вероятность попадания значений нормальной случайной величины за пределы довольно узкого интервала а ± 3σ составляет менее 0,3 %.

Формула ξ ~ N (а, σ²) используется как обозначение того, что случайная величина ξ имеет нормальное распределение с параметрами а и σ.

Если ξ ~ N (а, σ²), то для любых коэффициентов А, В случай мм величина, полученная умножением ξ на константу В и добавлением константы А, также является нормальной с параметрами:

А + Вξ ~ N(А + Ва, В²σ²).

Поэтому (ξ - а) / σ ~ N(0,1). Такое распределение называется стандартным нормальным. Плотность стандартного нормального распределения выражается формулой:

= .

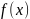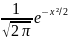Некоторые практически важные распределения, не являясь нормальными, могут быть сведены к нормальному путем определенных преобразований.

Логнормальное распределение. Непрерывная случайная величина ξ называется распределенной по логнормальному закону с параметрами а и σ², если случайная величина η = ln ξ распределена нормально с параметрами а и σ²(η ~ N (а, σ²)).

Логнормальные случайные величины могут принимать только положительные значения. На практике логнормальное распределение ти­пично для таких показателей, как концентрация различных загрязнителей в воздухе и в воде. Поэтому логнормальным распределением пользуются при оценке рисков, обусловленных загрязнением воздушной и водной среды, а в системах социально-гигиенического мониторинга часто используют не абсолютные величины концентраций загрязнителей, а натуральные логарифмы от них. В некоторых случаях такой подход оказывается эффективным и при мониторинге загрязнения почвы и оценке связанных с ним рисков.

Графики логнормального распределения при различных значениях параметров распределения приведены на рис. 4.8.

Экспоненциальным распределением называется распределение, функция плотности которого равна:

,

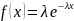при ,

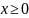где λ — положительный параметр (рис. 4.9).

Экспоненциальное распределение хорошо описывает распределение смертности в зависимости от возраста для детского населения. В этом случае функция распределения F(х) определяет риск смерти в возрасте х или раньше.

Распределения Вейбулла, Гомперца, Гомперца—Мейкема. Распределение Вейбулла было выведено для анализа продолжительности безотказ­ной работы многокомпонентных технических систем, но оно во многих

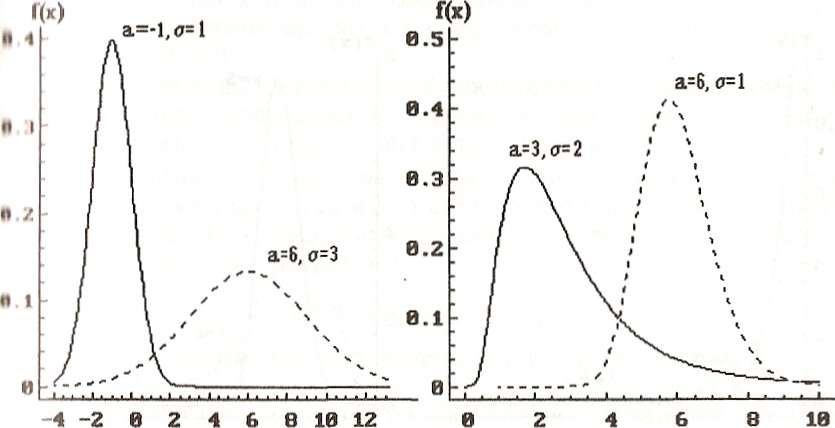
Рис. 4.7. Плотность нормального Рис. 4.8. Плотность логнормального

распределения распределения

случаях эффективно описывает зависимость риска смерти от возраста для взрослого населения. Функция распределения и функция плотности распределения Вейбулла имеют вид:

F( ) = 1 – ,

.

Распределение Вейбулла имеет два параметра (оба они являются положительными числами). Параметр λ называется параметром масштаба, поскольку его увеличение или уменьшение приводит, соответственно, к сжатию или растяжению графика функции плотности вдоль оси абсцисс. Параметр ν называется параметром формы. При его изменениях можно получить различные варианты формы функции плотности, в частности, при ν = 0 распределение Вейбулла совпадает с экспоненциальным распределением (рис. 4.10).

Более точное описание распределения риска смерти для взрослых дают другие виды распределений, широко используемые в демографии (рис. 4.11):

• двухпараметрическое распределение Гомперца с функцией плотности:

;

• трехпараметрическое распределение Гомперца—Мейкема:

,

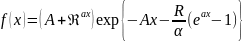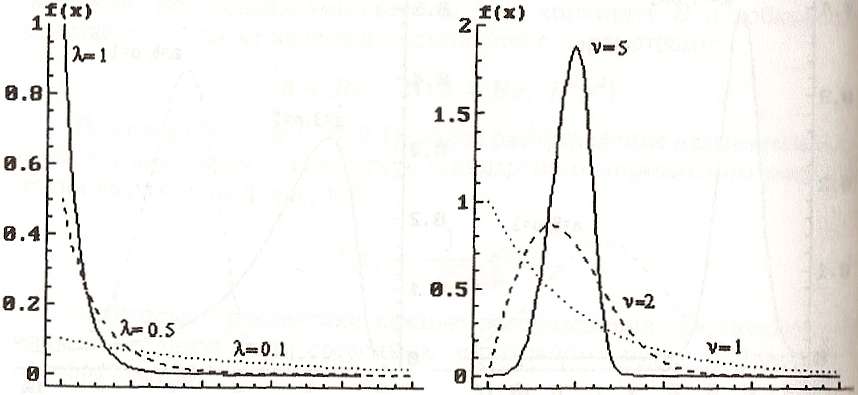
Рис. 4.9. Экспоненциальное Рис. 4. 10. Распределение

распределение Вейбулла с λ = 1

Распределение смертности по возрастам (данные из таблицы смертности для мужчин, СССР, 1968-1971 гг.) и ее аппроксимация с помощью плотности распределений Вейбулла, Гомперца и Гомперца-Мейкема

где A, R и α — положительные коэффициенты. Очевидно, что распределение Гомперца является частным случаем распределения Гомперца— Мейкема при А = 0.

Следующие виды распределений, построенные на основе стандартного нормального распределения, широко используются для проверки гипотез относительно нормальных случайных величин.

Распределение χ ² (хи-квадрат). Если каждая из n независимых случийных величин ξ₁, ξ₂, …, ξ_n имеет стандартное нормальное распределение (ξ_i ~ N(0, 1)), то распределение случайной величины η, представляющей собой сумму квадратов ξ_i:

+

называется хи-квадратом распределением с n степенями свободы (η ~ 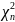) (рис. 4.12).

При оценке рисков данное распределение используется в случае, когда как фактор риска, так и показатели здоровья, по которым оценивается риск, имеют конечное число градаций (в наиболее простом случае фактор риска и негативный эффект имеют по две градации — присутствуют или отсутствуют). Соответствующие методы расчетов рас­сматриваются в §2.

Распределение Стъюдента (t - распределение). Если каждая из (n + 1) не зависимых случайных величин ξ₀, ξ₁, ξ₂, …, ξ_n распределена по нормальному закону с параметрами 0 и σ² (ξ ~ N(0, σ²)), то распределение случайной величины η, равной

называется распределением Стьюдента с n степенями свободы (η ~ t_n) (рис. 4.13).

Распределение Стьюдента является основой для наиболее популярного метода сравнения выборок (см. §3). Данный метод используется, в частности, для сравнения рисков при различных уровнях фактора риска в случае, если показатель здоровья, по которому определяется эффект фактора, представляет собой непрерывную величину.

Распределение Фишера (F - распределение). Если (п+m) независимых случайных величин ξ₁, ξ₂, …, ξ_n, ξ_n+1, ξ_n+m, распределены по нор­мальному закону с параметрами 0 и σ² (ξ_i ~ N(0, σ²)), то распределение случайной величины η, равной

η =

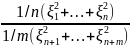
(n слагаемых в числителе и т — в знаменателе), называется распределением Фишера сnиm степенями свободы (η ~ F_n,m) (рис. 4.14).

Рис. 4.14. Распределение Фишера (F) с n, m степенями свободы

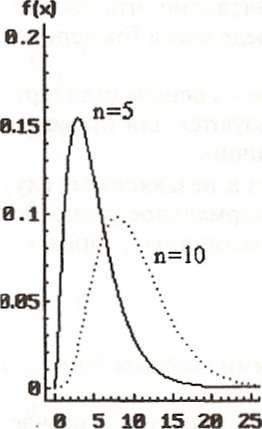
Рис. 4.12. Хи-квадрат распределение χ² с n степенями свободы

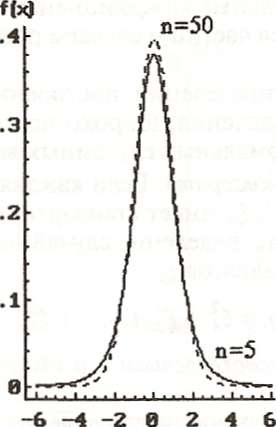
Рис. 4.13. Распределение Стьюдента (t) с n степенями свободы

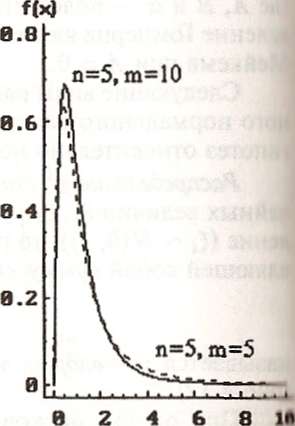
На этом распределении основан метод анализа рисков при различных уровнях фактора риска в случае, если фактор риска является дискретной величиной, а используемый для оценки риска показатель здоровья — непрерывной величиной (см. § 2).