2. Понятие вероятности

Понятие вероятности является базовым для количественного описания рисков при изучении влияния факторов окружающей среды на здоровье. Вероятность события — это мера, определяющая шанс появления этого события в испытаниях по сравнению с другими исходами. Риск определяется как вероятность неблагоприятных эффектов для здоровья человека или состояния окружающей среды. Формально - математически вероятность определяется следующим образом:

Для заданного пространства элементарных событий Ω вероятностью называется функция Р(А), определенная для любого события А и удовлетворяющая следующим условиям (аксиомам):

1. вероятность любого события неотрицательна:

P(A)≥ 0 для любого A;

2. вероятность достоверного (полного) события равна 1:

P(Ω) = 1;

3. для любой системы непересекающихся событий вероятность их объединения равна сумме вероятностей этих событий:

P(A₁ 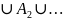) = P(A₁) + P(A₂) + … .

Из этих аксиом можно вывести следующие свойства вероятности:

- вероятность любого события лежит в интервале от 0 до 1:

1. ≤ P(A) ≤ 1 для любого A;

• вероятность пустого (невозможного) события равна 0:

P(ø) = 0

Если в качестве событий А₁, А₂,... рассматриваются различные последствия воздействия неблагоприятного фактора среды (например отсутствие последствий; возникновение заболеваний, связанных с данным фактором, в течение 1 года экспозиции; возникновение заболеваний, связанных с данным фактором, в течение жизни; смерть по причинам, связанным с данным фактором, и т.д.), то значения вероятностей для различных исходов служат характеристиками риска, обусловленного данным фактором. Для любой конкретной ситуации нетрудно убедиться, что вероятности отдельных исходов удовлетворяют всем приведенным выше свойствам вероятности. Например, если в качестве возможных исходов воздействия рассматривать перечень степеней тяжести заболевания, возникшего в результате этого воздействия (такой набор событий представляет собой полную систему), то очевидно, что для каждой степени тяжести величина риска находится в интервале между 0 и 1, а риск суммы нескольких исходов равен сумме рисков этих исходов.

2. Условная вероятность и связанные с ней понятия

Условная вероятность

Условной вероятностью события А при условии, что произошло событие В (обозначается как Р(А|В)), называется отношение вероятности пересечения событий А и В к вероятности события В (при условии, что Р(В)≠ 0):

P(A|B) =

Из этого определения следует формула умножения вероятностей:

P(AB) = P(A|B)P(B).

Событие А|В (событие А при условии В) можно интерпретировать как извлечение элемента, соответствующего событию АВ, из подмножества генеральной совокупности, соответствующего событию В. Доля таких элементов во всей генеральной совокупности равна Р(АВ), а в подмножестве В их доля, соответственно, в Р(В) раз меньше, т. е. равна Р(АВ)/Р(В). При оценке рисков часто используется следующее представление ситуации: в качестве события А рассматривается воздействие фактора риска, в качестве события В — неблагоприятный эффект для здоровья, тогда событие А|В соответствует появлению данного неблагоприятного эффекта при условии воздействия фактора риска.

Наиболее типичная сфера непосредственного применения понятий вероятности и условной вероятности — оценка рисков генетически обусловленных заболеваний. В ситуации, когда генотипы родителей таковы, что в потомстве возможны комбинации, обусловливающие определенные заболевания, важной задачей является оценка вероят­ности неблагоприятных вариантов генотипа будущего ребенка данной родительской пары на основе информации о генотипе родителей.

Пример 1. Какова вероятность того, что потомок родителей, гетерозиготных по некоторому гену, гомозиготен, если он имеет доминантный признак?

Решение. Доминантный признак в потомстве гетерозиготных родителей имеет место в случае трех комбинаций {АА, Аа, аА} из четырех равновероятных {АА, Аа, аА, аа}, т.е. вероятность его наличия равна 3/4. Гомозиготность при наличии доминантного признака соответствует единственному из этих 4 вариантов {АА}, поэтому вероятность пересечения событий {АА, Аа, аА} и {АА, аа} равна 1/4. Таким образом, искомая условная вероятность равна 1/4 : 3/4= 1/3.

Независимость событий

При анализе рисков часто требуется установить сам факт зависимости между исследуемым фактором риска и показателями здоровья. При анализе множественных факторов риска необходимо также учитывать возможные зависимости между ними (например, взаимосвязи между уровнями токсичного вещества в атмосферном воздухе, воде и почве, обусловленными общим источником загрязнения). Методы количественного анализа подобных эффектов основаны на следующем вероятностном определении независимости.

События А и В (оба имеющие ненулевую вероятность) называются независимыми, если вероятность их пересечения равна произведению их вероятностей:

P(AB) = P(A) P(B)

Из этого определения следует, что для независимых событий условная вероятность события А при условии В равна безусловной вероятности А:

P(A|B) =

Точно так же условная вероятность В при условии А равна безусловной вероятности В:

P(A|B) =

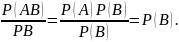
Более того, выполнение любого из условий Р(А|В) = Р(А) или Р(В|А) = Р(В) влечет за собой выполнение соотношения Р(АВ) = Р(А)Р(В), определяющего независимость, т.е. равенство условных вероятностей безусловным является необходимым и достаточным условием независимости событий. Поэтому на практике сравнение условных вероятностей с безусловными используют в целях выявления взаимозависимостей между определенными событиями, в частности, между под­верженностью действию некоторого фактора риска и заболеваемостью.

Используя данные вышеприведенного примера, рассмотрим методы определения взаимозависимости факторов с помощью приведенных выше формул.

Пример 2. Существует ли зависимость между наличием доминантного признака и гомозиготностью для потомства гетерозиготных родителей?

Решение. Проверку предположения о независимости событий можно провести двумя способами: используя непосредственно определение независимости или же путем сравнения условных вероятностей с безусловными. В первом случае отметим, что вероятность наличия доминантного признака равна 3/4 (как показано в примере 1), вероятность гомозиготности — 1/2, а вероятность пересечения этих событий — 1/4. Поскольку 1/4 ≠ 3/4 · 1/2, то события не являются независимыми. Условная вероятность гомозиготности при наличии доминантного признака равна, как показано в предыдущем примере, 1/3, т. е. отличается от безусловной вероятности гомозиготности, равной 1/2, откуда следует тот же вывод о зависимости событий.

Полная вероятность

Рассматриваемая здесь формула полной вероятности используется в целях оценки индивидуального риска в случае недостатка информации о величине воздействия на конкретного человека (например, если для конкретного случая воздействия фактора риска неизвестна экспозиция, но известны вероятности и величины последствий для всех возможных в данной ситуации уровней экспозиции).

Если события А₁, А₂,..., А_п образуют полную систему, то из условия их попарной независимости и полноты для любого события В формулу условной вероятности можно записать следующим образом:

P(B) = P(B|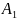 )P( ) + P(B| )P( ) + … + P(B|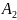 )P( ).

Эта формула называется формулой полной вероятности. Она используется для определения вероятности события В (например, возникновения заболевания у отдельного человека, подвергающегося воздействию некоторого фактора риска) в случае, когда об этом событии известны только его условные вероятности при условии реализации некоторого набора других событий, образующего полную систему (например, установленные в эпидемиологических исследованиях вероятности возникновения данного заболевания, соответствующие различным уровням этого фактора).

Пример 3. Некоторый фактор риска (событие А) имеет 3 различных уровня А₁, А₂, А₃, встречающиеся с частотой 60, 30 и 10% соответственно, причем вероятности возникновения заболевания, связанного с данным фактором (событие В), для этих уровней равны соответственно 50, 70 и 90%. Требуется оцепить вероятность заболевания для человека, подвергшегося воздействию фактора, при условии, что уровень воздействия неизвестен.

Решение. Для заданных условий P( ) = 0,6; P(A₂) = 0,3; P(A₃) = 0,1; P(B| ) = 0,5; P(B| ) = 0,7; P(B|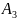 ) = 0,9. Тогда по формуле полной вероятности находим:

P(B) = 0,6 · 0,5 + 0,3 · 0,7 + 0,1 · 0,9 = 0,3 + 0,21 + 0,09 = 0,6.

Формула Байеса

Оценки риска тем более надежны, чем большее число наблюдений использовано для их вычисления. Накопление информации в процессе социально-гигиенического мониторинга позволяет постоянно уточнять ранее полученные оценки медицинских рисков. Уточнение оценок осуществляется с помощью так называемой формулы Байеса, кото­рая выводится из рассмотренных выше формул условной вероятности и формулы умножения вероятностей.

При решении задачи уточнения рисков исходные значения вероятностей событий А_i, т.е. Р(А_i), называются априорными (доопытными) вероятностями гипотез А_i, а полученные по формуле Байеса вероятности Р(А_i|В) — апостериорными (полученными в результате опыта, в котором наступило событие В) вероятностями гипотез А_i.

Формула Байеса выводится следующим образом. Из формулы умножения вероятностей имеем:

P( B) = P( |B)P(B) = P(B| )P( ),

Откуда

P( |B) = .

Подставляя в эту формулу выражение Р(В) из формулы полной вероятности, получим

P( |B) =

Эта формула называется формулой Байеса, или формулой вероятности гипотез, и используется для коррекции имеющейся информации о вероятности событий на основе результатов новых испытаний.

Пример 4. В примере 3 приведены оценки вероятностей для каждого из трех уровней фактора риска, т. е. априорные оценки, известные прежде, чем обследован еще один человек, подвергшийся воздействию данного фактора. Требуется определить уточненные (апостериорные) вероятности уровней фактора риска, если известно, что новый обследуемый заболел в результате воздействия данного фактора.

Решение. Формула Байеса дает следующие результаты:

P(A₁|B) = 0,6 · = 0,5,

P(A₂|B) = 0,3 · 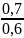= 0,35,

P(A₃|B) = 0,1 · 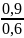= 0,15.

Таким образом, результат дополнительного наблюдения привел к уменьшению вероятности для наименее опасного уровня фактора риска и к увеличению вероятности для уровней, которым соответствует более высокая заболеваемость.

Задача 1. Вычислить апостериорные вероятности различных уровней фактора риска при условии, что обследуемый не заболел.

Решение. В задаче требуется определить апостериорные вероятности событий А₁, А₂, А₃ при условии отсутствия заболевания, т.е. события , являющегося дополнением к событию В.

P(A₁) = 0,6; P(A₂) = 0,3; P(A₃) = 0,1;

P(B̄) = 1 – P(B) = 0,4,

P(B̄|A₁) = 1 – P(B|A₁) = 0,5,

P(B̄|A₂) = 1 - P(B|A₂) = 0,3,

P(B̄|A₃) = 1 - P(B|A₃) = 0,1.

Тогда

P(A₁|B̄) = 0,6 · = 0,75,

P(A₂|B̄) = 0,3 · 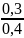= 0,225,

P(A₃|B̄) = 0,1 · 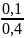= 0,025.

Таким образом, наблюдаемое отсутствие заболевания у обследуемого приводит к необходимости пересмотреть вероятность наименее опасного уровня фактора риска в сторону увеличения, а вероятности уровней, соответствующих более высоким вероятностям заболевания, — в сторону снижения.