
- •Физические основы механики, физика колебаний и волн, термодинамика
- •Содержание
- •Библиографический список……………………………………………….174 Приложение…………………………………………………………………175 Введение
- •Общие указания к выполнению лабораторных работ
- •Правила оформления отчета по лабораторным работам.
- •Требования к допуску, выполнению и защите лабораторных работ.
- •Лабораторная работа 1-01 Статистическая обработка результатов эксперимента. Случайные погрешности результатов наблюдений интервалов времени
- •Теоретическое введение
- •Методика измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Экспериментальная часть
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Методика измерений
- •Экспериментальная установка
- •Порядок выполнения работы
- •Контрольные вопросы
- •Экспериментальная часть
- •Экспериментальная установка
- •Порядок выполнения работы
- •Контрольные вопросы
- •Методика измерений
- •Экспериментальная часть
- •Порядок выполнения лабораторной работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Экспериментальная часть
- •Порядок выполнения работы
- •Контрольные вопросы
- •Экспериментальная часть
- •Порядок выполнения работы
- •Контрольные вопросы
- •Экспериментальная часть
- •Методика измерений
- •Порядок выполнения работы
- •Замечание 1: погрешность времени рассчитывается по стандартной методике расчета погрешностей случайной величины:
- •Контрольные вопросы
- •Экспериментальная установка и методика измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Используемые литература
- •Лабораторная работа 1-10 Изучение свободных колебаний пружинного маятника
- •Теоретическое введение
- •Экспериментальная часть
- •О писание установки
- •Обработка результатов измерений
- •Обработка результатов измерений
- •Контрольные вопросы
- •Цель работы: Определение жесткости пружины, определение периода свободных колебаний маятника с массивной пружиной.
- •Недостаточность модели 2
- •Экспериментальная часть
- •Описание установки
- •Порядок выполнения работы
- •Контрольные вопросы
- •Экспериментальная часть Математический маятник
- •Контрольные вопросы
- •Используемая литература
- •Лабораторная работа 1-13 Измерение момента инерции тела методом крутильных колебаний
- •Теоретическое введение
- •Экспериментальная часть
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Экспериментальная часть
- •Лабораторная установка и методика измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Экспериментальная установка и методика измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Экспериментальная часть
- •Методика измерений
- •Описание установки
- •Порядок выполнения работы
- •Контрольные вопросы
- •Экспериментальная часть
- •Порядок выполнения работы
- •Контрольные вопросы
- •Экспериментальная установка и методика измерений
- •Порядок выполнения работы
- •Обработка результатов
- •Контрольные вопросы
- •Экспериментальная часть
- •Порядок выполнения работы
- •Контрольные вопросы
- •Экспериментальная часть Экспериментальная установка и методика измерений
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Экспериментальная часть
- •Методика измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Методика измерений
- •Экспериментальная часть
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Экспериментальная часть
- •Порядок выполнения работы
- •Обработка результатов измерения
- •Контрольные вопросы
- •Используемая литература
- •Библиографический список
- •Приложение
Цель работы: Определение жесткости пружины, определение периода свободных колебаний маятника с массивной пружиной.
Теоретическое введение

Модель 1. Пружинный маятник с безмассовой пружиной
Рассмотрим свободные гармонические колебания на примере пружинного маятника – груза массой m, подвешенного на пружине с коэффициентом жёсткости k. Массой самой пружины обычно пренебрегают (см. лабораторную работу 1.18).
Пусть
длина недеформированной пружины (без
груза) равна
![]() ;
с грузом массой m
длина пружины в состоянии равновесия
равна l,
то есть увеличивается на
;
с грузом массой m
длина пружины в состоянии равновесия
равна l,
то есть увеличивается на
![]() (рис.11.1). Сила
упругости уравновешивается силой
тяжести:
(рис.11.1). Сила
упругости уравновешивается силой
тяжести:
![]() .
(11.1)
.
(11.1)
Груз,
выведенный из положения равновесия и
предоставленный сам себе, начинает
колебаться вдоль вертикальной оси. За
начало отсчёта удобно принять равновесное
положение груза, а ось OX
направить
вниз, то есть,
– это смещение груза из положения
равновесия,
![]() – его скорость. Изменение длины пружины
от первоначального недеформированного
состояния будет равно
– его скорость. Изменение длины пружины
от первоначального недеформированного
состояния будет равно
![]() .
Энергия системы складывается из
потенциальной энергии упругой деформации
пружины:
.
Энергия системы складывается из
потенциальной энергии упругой деформации
пружины:
![]() ,
(11.2)
,
(11.2)
потенциальной энергии груза в поле силы тяжести:
![]() (11.3)
(11.3)
и кинетической энергии груза:
![]() .
(11.4)
.
(11.4)
Полная механическая энергия системы при отсутствии сил трения (сопротивления среды) сохраняется:
![]() .
(11.5)
.
(11.5)
Продифференцируем (11.5) по времени:
![]() .
(11.6)
.
(11.6)
Поскольку
![]() ,
то после сокращения на
получим из (11.6):
,
то после сокращения на
получим из (11.6):
![]() ,
или
,
или
![]() ,
(11.7)
,
(11.7)
так
как
![]() .
С учётом (11.1)
получим из (11.7):
.
С учётом (11.1)
получим из (11.7):
![]() .
(11.8)
.
(11.8)
Разделив (11.8) на m, получим дифференциальное уравнение гармонических колебаний:
![]() .
(11.9)
.
(11.9)
Решением этого дифференциального уравнения является функция:
![]() ,
(11.10)
,
(11.10)
где
![]() – частота собственных колебаний маятника
с безмассовой пружиной. Период колебаний
такого маятника
– частота собственных колебаний маятника
с безмассовой пружиной. Период колебаний
такого маятника
![]() .
(11.11)
.
(11.11)
Заметим, что наличие поля силы тяжести не влияет на частоту колебаний пружинного маятника; изменяется лишь равновесное положение груза. Так что в дальнейшем потенциальную энергию в поле силы тяжести можно не учитывать.
Модель 2. Пружинный маятник с массивной пружиной
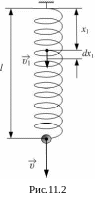
В некоторых случаях массой пружины пренебрегать нельзя. Найдём кинетическую энергию колеблющейся пружины. Пусть один конец однородной пружины массой M закреплен, а другой движется со скоростью υ (рис.11.2). Если растяжение равномерное, то скорость υ1 малого участка пружины длиной dx1 с координатой x1 равна:
![]()
 ,
(11.12)
,
(11.12)
где l – длина пружины в состоянии равновесия. Масса участка равна
![]() ,
(11.13)
,
(11.13)
а кинетическая энергия
![]() .(11.14)
.(11.14)
Проинтегрируем (11.14) по длине пружины:
![]()
![]() .
(11.15)
.
(11.15)
Теперь
при выводе дифференциального уравнения
колебаний маятника учтём энергию E1.
Полная механическая энергия пружинного
маятника с массивной пружиной равна
![]() ;
;
 .
(11.16)
.
(11.16)
Производная (11.16) по времени равна нулю, так как полная энергия сохраняется:
![]() ,
или после сокращения на скорость
,
или после сокращения на скорость
![]() ,
замены
и деления на
,
замены
и деления на
![]() :
:
![]() ;
;
 .
(11.17)
.
(11.17)
Дифференциальное
уравнение (11.17) подобно полученному выше
(11.9). Упростим модель, считая массу
пружины равной нулю, но к массе груза
добавим
![]() .
Это поправочное слагаемое называется
присоединенной массой пружины в
рассматриваемой задаче.
.
Это поправочное слагаемое называется
присоединенной массой пружины в
рассматриваемой задаче.
Запишем решением дифференциального уравнения (11.17):
![]() ,
(11.18)
,
(11.18)
где
 .
(11.19)
.
(11.19)
Период колебаний равен:
 .
(11.20)
.
(11.20)
