Тема 2 Система показателей статистики

Тесты:

1. По временному фактору показатель «Объем производства товаров и услуг» относится:

а) к моментному;

б) интервальному виду.

2. Соотношение одного и того же абсолютного показателя, характеризующего разные объекты, называется относительной величиной:

а) динамики;

б) структуры;

в) координации;

г) интенсивности;

д) сравнения.

3. «Общий коэффициент рождаемости» - относительный показатель:

а) динамики;

б) структуры;

в) координации;

г) интенсивности;

д) сравнения.

4. Абсолютные статистические показатели выражаются:

а) в процентах;

б) в именованных величинах;

в) в коэффициентах.

5. Если известны значения признака у каждой единицы совокупности и количество единиц, обладающих тем или иным значением признака, то применяется формула (запишите ее):

а) средняя гармоническая простая;

б) средняя арифметическая взвешенная;

в) средняя хронологическая;

г) средняя арифметическая простая.

6. Когда статистическая информация не содержит частот по отдельным единицам совокупности, а представлена как произведение этих единиц на значения признака, то применяется формула (запишите ее):

а) средняя гармоническая простая;

б) средняя арифметическая взвешенная;

в) средняя гармоническая взвешенная;

г) средняя геометрическая.

7. Модой в статистике называют:

а) значение признака у единицы, которая находится в середине упорядоченного ряда распределения;

б) значение признака, которое чаще всего встречается

в данной совокупности;

в) значение признака, которое встретилось в данной совокупности единственный раз.

8. Средняя из внутригрупповых дисперсий характеризует:

а) вариацию признака под влиянием всех факторов, формирующих уровень признака у единиц данной совокупности;

б) случайную вариацию, т.е. часть вариации, возникающую под влиянием других, неучтенных факторов, и не зависящую от признака-фактора, положенного в основание группировки;

в) различия в величине изучаемого признака, которые возникают под влиянием признака-фактора, положенного в основание группировки;

г) вариацию признака-результата, сложившуюся под влиянием изучаемого фактора.

9. Для измерения вариации значения признака не вычисляют:

а) медиану;

б) размах вариации;

в) среднее линейное отклонение.

10. Дисперсия вариационного ряда определяется как:

а) разность между наибольшим и наименьшим значениями признака;

б) средний квадрат отклонений вариантов от их средней арифметической;

в) сумма отклонений всех вариантов от их средней арифметической

Задача 1

По предприятию имеются данные о выпуске продукции за отчетный период:

№ предприятия фирмы	Выпуск продукции по плану млн. руб.	Процент выполнения плана по выпуску продукции
1 2 3	22,1 38,2 54,6	102,0 105,4 97,6

Определить:

20. Процент выполнения плана по выпуску продукции в целом по фирме;

21. Удельный вес предприятий в общем объеме фактического выпуска продукции.

Рекомендации по решению данного задания:

1. Фактический выпуск продукции по предприятиям фирмы:

Предприятие №1: 22,1 млн. руб. × 1,02 = 22,54 млн. руб.

Предприятие №2: 38,2 млн. руб. × 1,054 = 40,26 млн. руб.

Предприятие №3: 54,6 млн. руб. × 0,976 = 53,30 млн. руб.

Плановый выпуск, всего:

22,10 млн. руб. + 38,2 млн. руб. + 54,6 млн. руб. = 114,9 млн. руб.

Фактический выпуск, всего:

22,54 млн. руб. + 40,26 млн. руб. + 53,30 млн. руб. = 116,1 млн. руб.

Процент выполнения плана по выпуску продукции в целом по фирме:

116,1 млн. руб./114,9 млн. руб. × 100% = 101,0%

Итоговые сводные показатели представлены в таблице:

№ предприятия фирмы	Выпуск продукции по плану		Фактический выпуск продукции		Процент выполнения плана по выпуску продукции
	млн. руб.	процентов к итогу	млн. руб.	процентов к итогу
1 2 3	22,10 38,20 54,60	19,2 33,2 47,5	22,54 40,26 53,30	19,4 34,7 45,9	102,0 105,4 97,6
Итого	114,90	100,0	116,10	100,0	101,0

2. Удельные веса выпуска продукции каждого предприятия в общем выпуске:

Плановый удельный вес:

Предприятие №1: 22,1 млн. руб./114,9 млн. руб. × 100% = 19,2%;

Предприятие №2: 38,2 млн. руб./114,9 млн. руб. × 100% = 33,2%;

Предприятие №3: 54,6 млн. руб./114,9 млн. руб. × 100% = 47,5%.

Фактический удельный вес:

Предприятие №1: 22,54 млн. руб./116,1 млн. руб. × 100% = 19,4%

Предприятие №2: 40,26 млн. руб./116,1 млн. руб. × 100% = 34,7%;

Предприятие №3: 53,30 млн. руб./116,1 млн. руб. × 100% = 45,9%

Задача 2

Имеются данные о ценах и объемах выпуска одного вида продукции подразделениями предприятия:

№ подразделения	Цена за единицу продукции, руб.	Выручка от реализации продукции, тыс. руб.,
1 2 3 4	1343 1250 1295 1412	1477,3 1775,0 1890,7 1365,4
Итого	-	6508,4

Определить среднюю цену единицы продукции.

Рекомендации по решению данного задания:

Для определения средней цены, выведем логическую формулу:

Средняя цена определяется как отношение выручки от реализации к общему физическому объему реализации, то есть:

Из данной логической формулы известен объем выручки, то есть числитель и неизвестен объем, то есть знаменатель. Последний, может быть найден как частное от деления величины выручки на величину цены единицы продукции. Таким образом, получим формулу средней гармонической взвешенной. При расчете необходимо иметь ввиду, что цена единицы продукции выражена в рублях, а выручка в тысячах рублей.

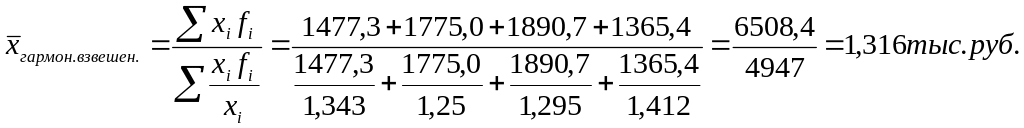Таким образом, средняя цена единицы продукции составила 1316 руб.

Задача 3

Имеются данные о стаже работы рабочих цеха:

Стаж работы, лет	Число рабочих
до 3 3-5 5-7 7-9 свыше 9	17 28 33 15 7
Итого	100

Определить:

1. Среднее линейное отклонение;

2. Дисперсию;

3. Среднее квадратическое отклонение;

4. Коэффициент вариации.

Рекомендации по решению данного задания:

Расчет показателей вариации проведем в таблице:

Стаж работы, лет	Середины интервалов,	Число рабочих,
до 3 3-5 5-7 7-9 свыше 9	2 4 6 8 10	17 28 33 15 7	3,3 1,3 0,7 2,7 4,7	56,1 36,4 23,1 40,5 32,9	185,13 47,32 16,17 109,35 154,63
Итого	-	100	-	189	512,6

Средний арифметический стаж работы равен 5,3 лет, то есть =5,3.

1. Среднее линейное отклонение

Поскольку, исходные данные сгруппированы, то используется формула:

2. Дисперсия

3. Среднее квадратическое отклонение

4. Коэффициент вариации

Полученное высокое значение коэффициента вариации говорит о количественной неоднородности совокупности и о не типичности полученного среднего стажа работы.

Текущий контроль по данной теме проводится на седьмом практическом занятии.