Тема 6. Показатели вариации
Средние величины раскрывают важную обобщающую характеристику совокупности по варьирующему признаку. Рассчитав их, необходимо уяснить, насколько они показательны, типичны или однородны. Одинаковые средние могут характеризовать, совершенно разнородные совокупности. Провести оценку однородности совокупности, а также типичности средней величины можно с помощью расчета показателей вариации.
Вариация признака - это изменение значений признака у единиц статистической совокупности, которые обусловлены влиянием действия различных факторов.
Применение показателей вариации в экономическом анализе достаточно широко: они рассчитываются для статистических совокупностей упорядоченных с помощью метода группировок, классификаций, построения рядов распределения и позволяют оценить колебания значений изучаемого признака, однородность совокупности по данному признаку.
Существуют две группы показателей вариации:
- абсолютные;
- относительные.
Абсолютные показатели вариации.
Абсолютная величина, с помощью которой измеряется вариация признака, - размах вариации.
Размах вариации (R) - это разность между наибольшим и наименьшим значениями признака.
Определяется размах вариации следующим образом:
где
- наибольшее и наименьшее значение
признака в изучаемой совокупности;
Величина размаха вариации зависит от крайних значений признака и не отражает колеблемости признака у основной массы единиц совокупности.
В ряде случаев, возникает необходимость в расчете показателя, который будет отражать вариацию значений признаков от их средней (общей) величины. К таким показателям относятся:
среднее линейное отклонение;
дисперсия;
среднее квадратическое отклонение.
Вышеуказанные показатели вариации представляют собой средние величины, полученные из отклонений индивидуальных значений признака от их среднего.
Среднее линейное отклонение дает обобщенную характеристику степени колеблемости признака в совокупности и вычисляется для несгруппированных и сгруппированных данных по следующим формулам:
а) для не сгруппированных данных (простое):
б) для сгруппированных данных (взвешенное):
где - варианта;
- средний уровень
изучаемого ряда распределения;
- частота.
Среднее отклонение случайной величины от ее математического ожидания равно нулю, в практике обычно используют другой показатель, а именно дисперсия. Дисперсия - это средний квадрат отклонений индивидуальных значений признака от их средней величины, который в зависимости от исходных данных рассчитывается по формулам простой дисперсии (для несгруппированных данных) и взвешенной дисперсии (для сгруппированных данных):
а) для не сгруппированных данных (простое):
б) для сгруппированных данных (взвешенное):
Формула дисперсии также может быть записана в следующем виде:
Для несгруппированных данных преобразованная формула для определения дисперсии имеет вид:
,
для сгруппированных:
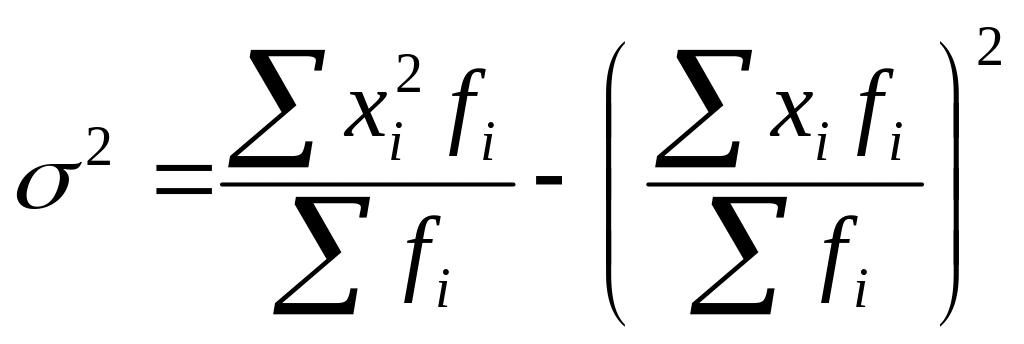
Среднее квадратическое отклонение рассчитывается как корень квадратный из дисперсии. Эта величина также вычисляется как простая или взвешенная в зависимости от того, каковы исходные данные - сгруппированные или несгруппированные:
Преобразуем вышеуказанную формулу среднего квадратического отклонения:
а) для не сгруппированных данных (простое):
б) для сгруппированных данных (взвешенное):
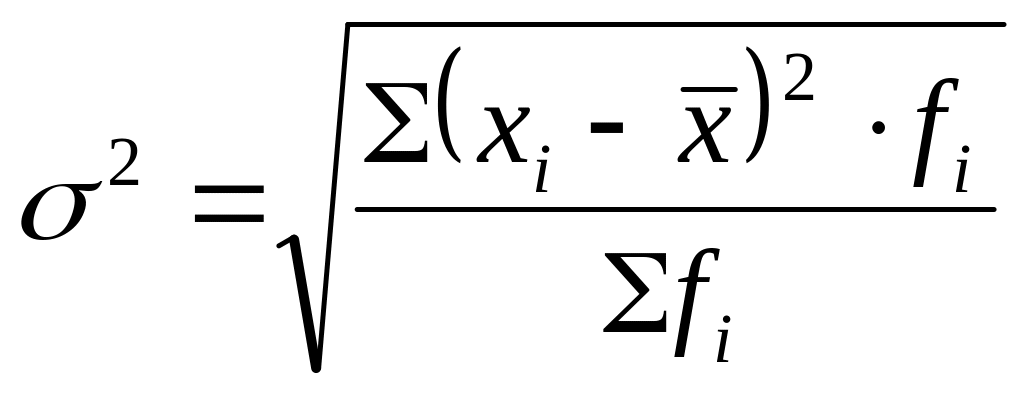
2. Относительные показатели вариации характеризуют колеблемость изучаемых признаков в совокупности или одного и того же признака в нескольких совокупностях. Эти показатели исчисляются в виде отношения (в %) абсолютного показателя вариации к средней арифметической. Существуют следующие относительные показатели вариации:
а) Коэффициент вариации:
Чем меньше значение коэффициента вариации, тем более однородна совокупность и, тем более типичен рассчитанный средний уровень ряда.
б) Коэффициент осцилляции:
В статистической совокупности, разбитой на однородные группы по какому-либо признаку, общая вариация складывается из внутригрупповой и межгрупповой вариации. В данном случае, в силу вступает правило сложения дисперсий. Общая дисперсия, в соответствии с этим правилом может быть рассчитана по формуле:
где
- средняя из внутригрупповых дисперсий
(
- внутригрупповая дисперсия в j-й
группе,
- численность j-й
группы);
- межгрупповая
дисперсия (
-
групповые средние,
- общая средняя изучаемого показателя).
Дисперсия доли определяется двумя способами:
а) путем определения общей дисперсии доли по формуле:
где
- средняя доля.
б) путем применения правила сложения дисперсий:
Дисперсия доли определяется по формуле:
где
- доля изучаемого признака.
Отсюда, средняя из внутригрупповых дисперсий доли, определяется по формуле:
Межгрупповая дисперсия определяется:
Далее для нахождения общей дисперсии используется уже известное правило сложения дисперсий.
С помощью перечисленных показателей можно определить эмпирическое корреляционное отношение (η – «эта»), которое используется для оценки силы влияния группировочного признака на общую вариацию признака, или для оценки тесноты зависимости результативного признака от группировочного признака. Данный показатель рассчитывается по формуле:
