меньшее значение, а статистика модифицированный R2 – большее. Следовательно, усложнение модели было целесообразно.
Модель №3
Дополним модель остальными интервальными переменными. Приведем результаты расчетов.
Таблица 11 Результаты оценивания модели № 2 без фиктивных переменных
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
-9128.406 |
2621.563 |
-3.482047 |
0.0006 |
WEIGHT |
18.51954 |
2.040387 |
9.076484 |
0.0000 |
YIELD_M |
0.474008 |
0.084655 |
5.599311 |
0.0000 |
FAT |
-662.9292 |
445.0309 |
-1.489625 |
0.1379 |
FAT_M |
998.0067 |
537.1793 |
1.857865 |
0.0647 |
R-squared |
0.478971 |
Mean dependent var |
4627.630 |
|
Adjusted R-squared |
0.468283 |
S.D. dependent var |
1265.533 |
|
S.E. of regression |
922.8137 |
Akaike info criterion |
16.51741 |
|
Sum squared resid |
1.66E+08 |
Schwarz criterion |
16.59987 |
|
Log likelihood |
-1646.741 |
F-statistic |
|
44.81477 |
Durbin-Watson stat |
1.816958 |
Prob(F-statistic) |
0.000000 |
|
|
|
|
|
|
|
|
|
|
10000 |
|
|
|
|
|
|
|
|
|
8000 |
|
|
|
|
|
|
|
|
|
6000 |
6000 |
|
|
|
|
|
|
|
|
4000 |
4000 |
|
|
|
|
|
|
|
|
2000 |
2000 |
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
-2000 |
|
|
|
|
|
|
|
|
|
-4000 |
|
|
|
|
|
|
|
|
|
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
|
Residual |
Actual |
|
Fitted |
|
|||
Рисунок 9. Визуальный анализ качества модели №3. |
|||||||||
Отметим, что данный рисунок мало отличается от Рисунка 5, в частности, расположение выбросов приблизительно одинаковое.
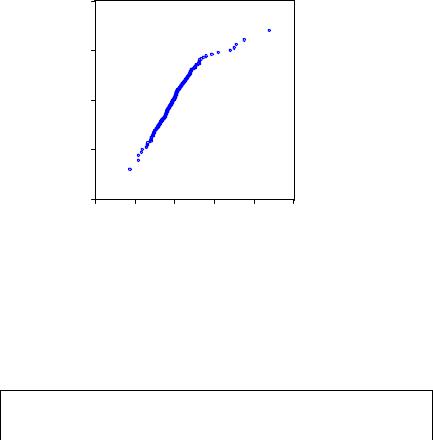
Normal Quantile
4
2
0
-2
-4 -4000 -2000 0 2000 4000 6000
RESID
Рисунок 10. Анализ вида распределения с помощью нормальной кривой в модели №3
Данный рисунок также напоминает Рисунок 6. Существенных изменений характера распределения не наблюдается.
Таблица 12 Анализ наличия гетероскедастичности в модели №3
White Heteroskedasticity Test:
F-statistic |
1.332161 |
Probability |
0.191879 |
Obs*R-squared |
18.31596 |
Probability |
0.192767 |
Используя тот же критерий, что и в моделях №1 и 2 мы можем отметить, что гипотеза об отсутствии гетероскедастичности не отклоняется. С учетом того, что статистика Дарбина – Уотсона близка к 2, мы можем заключить, что значимость оценок, скорее всего, определена верно.
Рассмотрим последствия включения в модель данных о жирности. В полном соответствии с результатами визуального анализа и анализа корреляционных матриц мы видим, что при выполнении гипотезы о нормальности случайной составляющей, трудно определить силу влияния жирность молока на удой (p=0.1379). Отметим только, что знак оценки соответствующего коэффициента отрицательный, т.е., возможно, корова, дающая более жирное молоко, менее производительна.
Выводы о влиянии жирности молока матери, видимо, более определенны (p=.0.0647). Более жирное питание в детстве приводит к большим надоям. Тем не менее, точность оценки коэффициента недостаточна для уверенного включения этого показателя в модель. Кроме того, этот результат противоречит результатам визуального анализа и анализа корреляционных матриц.
Отметим, что значение статистики Шварца несколько увеличилось
Schwarz criterion=16.59987 (16.56828), но, поскольку, в то же время значение статистики Акаики уменьшилось Akaike info criterion=16.51741 (16.51880),
можно пренебречь этим изменением. Значение модифицированного R2
увеличилось Adjusted R-squared=0.468283 (0.462303), но незначительно. Таким образом, качество модели с точки зрения точности подгонки и сложности изменилось не существенно.
В заключение проверим гипотезу об одновременном равенстве нулю коэффициентов при новых переменных с помощью критерия Вальда.
Таблица 13 Проверка гипотезы об одновременном равенстве нулю коэффициентов
при переменных «Жирность» и «Жирность_М».
Null Hypothesis: |
C(4)=0 |
|
|
|
|
C(5)=0 |
|
|
|
F-statistic |
2.107671 |
|
Probability |
0.124281 |
Chi-square |
4.215342 |
|
Probability |
0.121521 |
Видно, что обе статистики не позволяют отвергнуть основную гипотезу на 5% уровне, т.к. Probability > 0.05. Следовательно, данные о жирности молока матери и потомства мы пока не будем включать в модель.
Модель №4
Рассмотрим еще один интересный вариант линейной регрессии. Можно предположить, что «Вес» - неоднозначная характеристика продуктивности коровы. Мы уже знаем, что удои матери – значимая характеристика продуктивности дочернего животного. Две коровы с приблизительно одинаковым весом будут, возможно, обладать различной продуктивностью, в зависимости от условий, в которых они росли. Если в детстве животное получало достаточно питания, т.е. удои матери были высокие, то она будет обладать более высокой продуктивностью, чем корова, набравшая вес во взрослом состоянии. Проверим это предположение. С точки зрения модели оно сводится к тому, что коэффициент линейной регрессии для веса зависит от удоев матери. Например, это может выглядеть так:
yield = c + (a +b * yield _ m) * weight + v = c + a * weight +b * yield _ m * weight + v
. Результаты расчетов показывают следующее. Таблица 14 Результаты оценивания модели № 4
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
C |
-5859.102 |
1122.530 |
-5.219551 |
0.0000 |
WEIGHT |
15.27737 |
2.279990 |
6.700631 |
0.0000 |
WEIGHT*YIELD_M |
0.000754 |
0.000135 |
5.601997 |
0.0000 |
R-squared |
0.471244 |
Mean dependent var |
4627.630 |
|
Adjusted R-squared |
0.465876 |
S.D. dependent var |
1265.533 |
|
S.E. of regression |
924.9002 |
Akaike info criterion |
16.51214 |
|
Sum squared resid |
1.69E+08 |
Schwarz criterion |
16.56161 |
|
Log likelihood |
-1648.214 |
F-statistic |
|
87.78619 |
Durbin-Watson stat |
1.877016 |
Prob(F-statistic) |
0.000000 |
|
|
|
|
|
|
|
|
|
|
10000 |
|
|
|
|
|
|
|
|
|
8000 |
|
|
|
|
|
|
|
|
|
6000 |
6000 |
|
|
|
|
|
|
|
|
4000 |
4000 |
|
|
|
|
|
|
|
|
2000 |
2000 |
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
-2000 |
|
|
|
|
|
|
|
|
|
-4000 |
|
|
|
|
|
|
|
|
|
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
|
Residual |
Actual |
|
Fitted |
|
|||
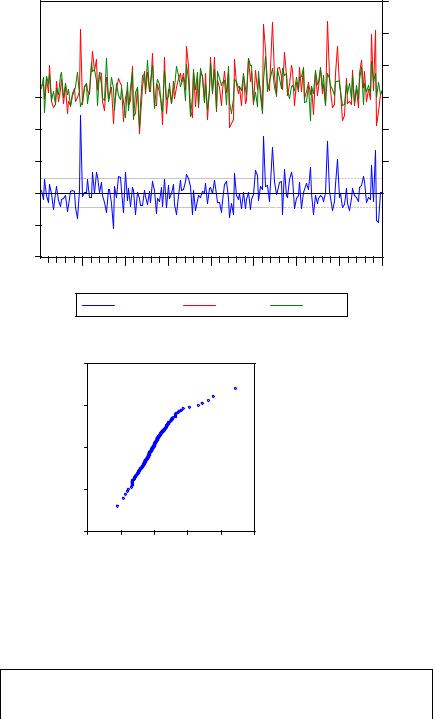
Рисунок 11. Визуальный анализ качества модели №4
Normal Quantile
4
2
0
-2
-4 -4000 -2000 0 2000 4000 6000
RESID
Рисунок 12. Анализ вида распределения с помощью нормальной кривой в модели №4
Таблица 15 Анализ наличия гетероскедастичности в модели №3
White Heteroskedasticity Test:
F-statistic |
0.121728 |
Probability |
0.987430 |
Obs*R-squared |
0.625500 |
Probability |
0.986806 |
Видно, что качество модели, судя по основным характеристикам, мало изменилось по сравнению с моделью №2, но все оценки значимы. Таким образом, эта модель также имеет право на существование. Фактически образовавшаяся новая переменная WEIGHT*YIELD_M, носит название «взаимодействие».