Разведочный анализ данных
Теоретические основания
До построения модели следует провести разведочный анализ собранной информации (набора данных). Целью анализа является формулирование гипотез о характере зависимости «зависимой» переменной от «независимых». Все предположения и выводы, формулируемые в работе не должны противоречить здравому смыслу.
Предполагается, что каждый элемент выборки получен случайным образом, и выборка удовлетворяет условию репрезентативности, то есть в ней пропорционально представлена генеральная совокупность [1, 2].
Разведочный анализ данных начинается с визуального анализа. Одним из наиболее распространенных методов визуального анализа выборок является построение диаграммы рассеяния. Это простой и наглядный инструмент. По расположению точек на диаграмме мы сможем сделать предположения как о возможной зависимости между переменными, так и о характере этой зависимости. Для построения диаграммы рассеяния достаточно выбрать интересующую пару переменных X = (X1,..., XT ) и Y = (Y1 ,... ,YT ) , каждому
наблюдению выборки сопоставить пару точек (X1, Y1 ),..., (XT , YT ) и затем
нанести эти пары точек на координатную плоскость. Если между переменными имеется зависимость, то ее можно увидеть по расположению точек на диаграмме. Например, в случае линейной зависимости между переменными X и Y, точки на диаграмме будут “сгущаться” около некоторой гипотетической прямой.
Известно, что мерой линейной зависимости между двумя случайными величинами служит коэффициент корреляции Пирсона ρ. Выборочным аналогом коэффициента корреляции Пирсона является выборочный коэффициент корреляции r, который вычисляется следующим образом:
Пусть имеется набор из двух переменных X = (X1,..., XT ) и Y = (Y1,... ,YT ) .
|
|
|
|
1 |
T |
|
|
|
|
1 |
T |
|
|
|
= |
∑X t и |
|
|
|
∑Yt , соответственно выборочные средние, тогда |
|||||
X |
Y |
= |
||||||||||
|
T |
|
|
|||||||||
|
|
|
t =1 |
|
|
|
T t =1 |
|||||
выборочный коэффициент корреляции Пирсона вычисляется по формуле:
|
T |
|
|
∑(X t−X )(Yt −Y ) |
|
r(X , Y ) = |
t =1 |
|
T |
T |
|
|
∑(X t−X )2 |
∑(Yt −Y )2 |
|
t =1 |
t =1 |
Предположим, что наблюдаются две случайные величины и выборочный коэффициент корреляции рассматривается в качестве оценки истинного. Рассмотрим задачу проверки гипотезы о том, что теоретический коэффициент корреляции равен нулю в случае, когда наблюдения имеют нормальное совместное распределение. Справедливость этой гипотезы означает, что регрессор не влияет на зависимую переменную. Предположение о
нормальности дает возможность построить критерий. Сформулируем пару гипотез – основная гипотеза Н0: ρ(X , Y )=0, альтернативная Н1: ρ ( X , Y ) ≠0 .
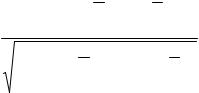
Статистика критерия |
имеет вид t = r |
T −2 . Критическая область |
|
|
|
|
1−r 2 |
образована |
двумя лучами, |
ограниченными |
значениями ±t1−α / 2 (T −2), где |
t1−α / 2 (T − 2) |
- квантиль распределения Стьюдента с T – 2 степенями свободы |
||
порядка 1−α / 2 . Проверка гипотезы совместной нормальности выходит за рамки данной работы.
Проведение визуального анализа Минимальные требования
Необходимо построить и проанализировать диаграммы рассеяния для одной пары – (зависимая переменная, независимая переменная) при двух уровнях номинальной переменной.
Анализ диаграмм рассеяния
Для каждого сочетания переменной Удой с переменными Жирность, Вес, Удой_М, Жирность_М построим диаграмму рассеяния (scatterplot). По оси OY будем откладывать значения переменной Удой. Для построения графиков удобнее объединять соответствующие пары в группы и использовать соответствующие атрибуты этих объектов.
YIELD
10000
race=1
8000
6000 |
|
|
|
|
|
|
4000 |
|
|
|
|
|
|
2000 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
3.2 |
3.4 |
3.6 |
3.8 |
4.0 |
4.2 |
4.4 |
FAT
YIELD
10000
race=2
8000
6000
4000
2000
0 |
|
|
|
|
|
3.2 |
3.4 |
3.6 |
3.8 |
4.0 |
4.2 |
FAT
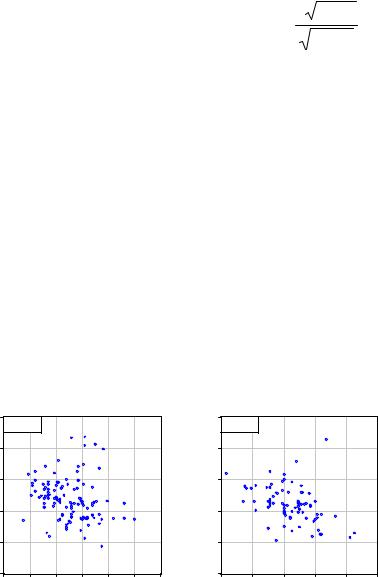
График 1. Зависимость удоя от жирности.
Обратим внимание на то, что наблюдения, относящиеся к чистопородным и не чистопородным животным перемешаны. Наверно, для данной выборки Удой и Жирность мы не можем ни подтвердить ни отвергнуть предположение об их зависимости от породы. Мы еще раз вернемся к этим предположениям 1 и 2 при проведении регрессионного анализа.
Отметим, что точки наблюдений сильно разбросаны по диаграмме. Однако некоторую зависимость в расположении точек все же можно уловить. Чтобы немного прояснить картинку, отметим для себя особенно выделяющиеся из основной массы наблюдения. Для них характерны большие показатели удоя в сочетании с большой жирностью производимого молока. Видимо, в жизни такие случаи довольно редки. Но, если в данных все же присутствуют такие наблюдения, то при выполнении реальной (не учебной) работы лучше
проконсультироваться со специалистом в предметной области об их происхождении.
Теперь еще раз посмотрим на График 1. По расположению точек на диаграмме можно предположить, что существует не очень сильная отрицательная зависимоть между величиной удоя коровы и величиной жирности ее молока. Это наблюдение согласуется с предположением 5.
Рассмотрим следующую зависимость.
YIELD
10000
race=1
8000
6000
4000
2000
0 |
|
|
|
|
450 |
500 |
550 |
600 |
650 |
YIELD
10000
race=2
8000
6000
4000
2000
0 |
|
|
|
|
450 |
500 |
550 |
600 |
650 |
WEIGHT |
WEIGHT |
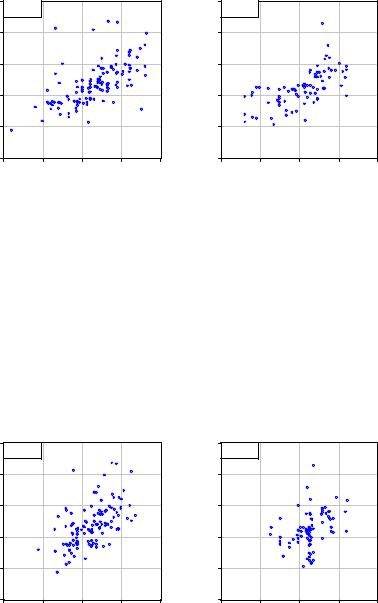
График 2. Зависимость удоя от веса.
На Графике 2 точки наблюдений расположены более тесно по сравнению с Графиком 1. Благодаря этому, можно предположить положительную зависимость величины удоя коровы от ее массы. На наш взгляд это наблюдение говорит в пользу предположения 3. Отметим также, что для чистопородных коров положительная зависимость удоя от веса прослеживается более четко.
Теперь посмотрим на График 3. Сопоставление удоя коровы с удоем ее матери говорит о том, что между этими переменными возможно существует положительная зависимость. Отметим, что данная зависимость наиболее четко прослеживается для чистопородных коров.
YIELD
10000
race=1
8000
6000
4000
2000
0
0 |
2000 |
4000 |
6000 |
8000 |
YIELD
10000
race=2
8000
6000
4000
2000
0
0 |
2000 |
4000 |
6000 |
8000 |
YIELD_M |
YIELD_M |
График 3 Зависимость удоя коровы от удоя матери.
Рассмотрим диаграммму рассеяния для пары (Удой, Жирность_М) (График 4). Как и в случае (Удой, Жирность), здесь можно предположить отрицательную зависимость. Однако, точки на диаграмме довольно сильно разбросаны и зависимость слабо выражена.
YIELD
10000
race=1
8000
6000
4000
2000
0 |
|
|
|
|
|
3.4 |
3.6 |
3.8 |
4.0 |
4.2 |
4.4 |
FAT_M
YIELD
10000
race=2
8000
6000
4000
2000
0 |
|
|
|
|
|
3.2 |
3.4 |
3.6 |
3.8 |
4.0 |
4.2 |
FAT_M
График 4 Зависимость удоя от жирности молока матери Тем не менее, для чистопородных коров зависимость видна более
отчетливо.
Построив несколько диаграмм рассеяния, мы получили предварительное представление о виде интересующей нас зависимости между переменными. Сопоставление диаграмм рассеяния позволяет предположить, что чистопородность влечет за собой более яркую выраженность связи и, таким образом для одной и той же модели, для чистопородных коров дисперсия случайной составляющей будет меньше.
Проведение корреляционного анализа Минимальные требования
Необходимо проанализировать значимость оценки коэффициента корреляции Пирсона для одной пары (зависимая переменная, независимая переменная) в предположении о нормальном совместном распределении.
Анализ значимости оценок коэффициентов корреляции Пирсона
Проанализируем силу линейной зависимости «зависимой» переменной от «независимых». Для этого воспользуемся описанным выше критерием для проверки гипотезы о равенстве нулю значения коэффициента корреляции Пирсона для всех пар (зависимая переменная, независимая переменная). Объединим интересующие нас переменные в группу (group all yield fat fat_m weight yield_m) и оценим соответствующие корреляционные матрицы для всех данных (‘cm_all’), чистопородных (‘cm1’) и нет (‘cm2’) коров (например, sym cm_all=@cor(all)).
Таблица 1 Оценка корреляционной матрицы переменных участвующих в анализе для
чистопородных коров.
|
yield |
fat |
fat_m |
weight |
yield_m |
yield |
1.000000 |
-0.182282 |
-0.288074 |
0.604109 |
0.555087 |
Fat |
-0.182282 |
1.000000 |
0.468880 |
-0.201144 |
-0.248111 |
fat_m |
-0.288074 |
0.468880 |
1.000000 |
-0.334483 |
-0.552072 |
weight |
0.604109 |
-0.201144 |
-0.334483 |
1.000000 |
0.372088 |
yield_m |
0.555087 |
-0.248111 |
-0.552072 |
0.372088 |
1.000000 |
Таблица 2 Оценка корреляционной матрицы переменных участвующих в анализе для
не чистопородных коров.
|
yield |
fat |
fat_m |
weight |
yield_m |
yield |
1.000000 |
-0.412747 |
-0.207091 |
0.640927 |
0.361488 |
fat |
-0.412747 |
1.000000 |
0.294695 |
-0.434164 |
-0.141576 |
fat_m |
-0.207091 |
0.294695 |
1.000000 |
-0.297818 |
-0.415815 |
weight |
0.640927 |
-0.434164 |
-0.297818 |
1.000000 |
0.360778 |
yield_m |
0.361488 |
-0.141576 |
-0.415815 |
0.360778 |
1.000000 |
Таблица 3 Оценка корреляционной матрицы переменных участвующих в анализе для
всей выборки.
|
yield |
fat |
fat_m |
weight |
yield_m |
yield |
1.000000 |
-0.234023 |
-0.230365 |
0.622103 |
0.486289 |
fat |
-0.234023 |
1.000000 |
0.426397 |
-0.243712 |
-0.214953 |
fat_m |
-0.230365 |
0.426397 |
1.000000 |
-0.275361 |
-0.498870 |
weight |
0.622103 |
-0.243712 |
-0.275361 |
1.000000 |
0.354758 |
yield_m |
0.486289 |
-0.214953 |
-0.498870 |
0.354758 |
1.000000 |
Вприведенных таблицах нас в первую очередь интересует первая строка (столбец). Значение статистики критерия легко подсчитать вручную, но можно воспользоваться следующими командами EViews (пример для Таблицы 3 при вероятности ошибки первого рода 5%).
scalar t_all=@obs(yield) scalar p=0.05
scalar bnd= @qtdist(1-p/2,t_all-2) matrix (4,2) rost_all
for !i=1 to 4
rost_all(!i,1)=cm_all(!i+1,1)*@sqrt(t_all-2)/@sqrt(1- cm_all(!i+1,1)^2) rost_all(!i,2)= 1-@ctdist(@abs(rost_all(!i,1)),t_all-2)
next
Врезультате мы получим следующие значения статистик:
Таблица 4 Значения статистик для критерия проверки гипотезы о равенстве нулю
коэффициента корреляции для всей выборки
|
Статистика критерия |
p-уровень |
fat |
-3.387043 |
0.000426 |
fat_m |
-3.331114 |
0.000516 |
weight |
11.18070 |
0.000000 |
yield_m |
7.830973 |
1.44E-13 |
Таблица 5 Значения статистик для критерия проверки гипотезы о равенстве нулю
коэффициента корреляции для чистопородных коров.
|
Статистика критерия |
p-уровень |
fat |
-2.005282 |
0.023620 |
fat_m |
-3.253942 |
0.000744 |
weight |
8.199798 |
1.75E-13 |
yield_m |
7.218362 |
2.85E-11 |